Внецентренное сжатие (растяжение) – вид сложного сопротивления, при котором внешняя сжимающая (растягивающая) сила действует параллельно оси бруса, но точка приложения силы не совпадает с центром тяжести поперечного сечения.
Простейший случай внецентренного сжатия в строительстве – действие сосредоточенной силы на колонну так, что точка приложения находится вне центра тяжести поперечного сечения колонны (в любой произвольной точке поперечного сечения).
Основное отличие внецентренного сжатия от внецентренного растяжения – в направлении приложенной силы. Ограничимся рассмотрением внецентренного сжатия (рис. 3.1).
| Рис. 3.1 |
| a) |
| б) |
| y |
| z |
| F |
| x |
| О |
|
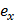
| y |
| x |
|
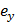
На рис. 3.1, б точкой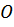 
показана точка приложения сжимающей силы в плоскости поперечного сечения, точка 
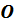– полюс. Координаты полюса 
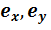– эксцентриситеты приложенной силы относительно главных центральных осей инерции.
17
Внецентренное приложение силы обусловливает то, что в поперечных сечениях стержня возникает не только продольная сила, но и изгибающие моменты в двух плоскостях. Принято считать, что в поперечном сечении возникают три внутренних силовых фактора (ВСФ):
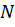– продольная сила;
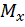– изгибающий момент в плоскости YZ;
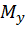– изгибающий момент в плоскости XZ.
В каждом сечении может возникать и поперечная сила, но ее действием при расчете нормальных напряжений пренебрегают.
Определение нормальных напряжений
В общем случае внецентренного растяжения и сжатия нормальные напряжения рассчитываются по формуле
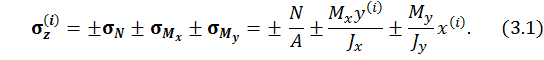
В нашем случае рассматриваем внецентренное сжатие, поэтому всегда имеем знак минус в первом слагаемом:
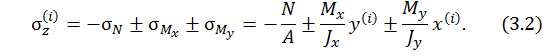
Внутренние силовые факторы, очевидно, вычислим следующим образом:
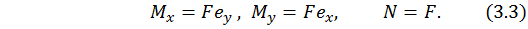
Тогда формулу (3.2) с учетом (3.3) можно переписать в виде
18
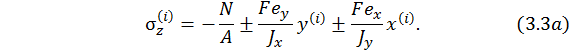
Вынесем за знак скобки общий множитель, получим окончательный вид формулы:
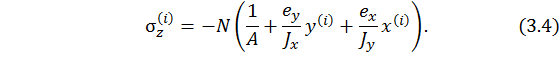
Таким образом, формула (3.2) или она же в виде формулы (3.4) позволяет вычислить нормальные напряжения в любой точке поперечного сечения.
§ 3.3. Расчет на прочность при внецентренном
Сжатии (растяжении)
Расчет на прочность проводится в опасных точках поперечного сечения. Поэтому практический интерес представляют именно эти точки. Как и при косом изгибе, опасными являются точки, наиболее удаленные от нейтральной линии.
При внецентренном сжатии (растяжении) нейтральная линия не проходит через центр тяжести поперечного сечения, а отсекает на главных центральных осях отрезки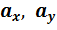 
.
Определим длины отрезков, которые отсекает нейтральная линия в поперечном сечении.
Первоначально введем понятие новых для нас геометрических характеристик.
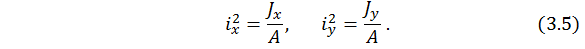
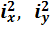– квадраты радиусов инерции поперечного сечения.
Выражение (3.4) перепишем с учетом (3.5). При этом второе и третье слагаемое умножим и разделим одновременно на параметр площади поперечного сечения A.
19
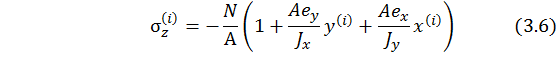
Далее в записи (3.6) вынесем общий множитель, окончательно получим выражение нормальных напряжений в виде
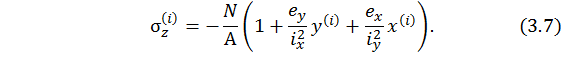
Пусть некоторая произвольная точка принадлежит нейтральной линии. Обозначим ее координаты 
. Подставим эти координаты в равенство (3.7) и приравняем его нулю. Тогда получим уравнение нейтральной линии в виде
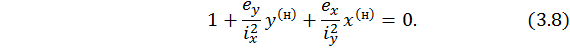
По уравнению (3.8) можно определить отрезки, которые НЛ отсекает на главных центральных осях поперечного сечения.
1) Пусть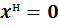 
, т.е. будем рассматривать точку, которая принадлежит оси у. Из уравнения (8) получим:
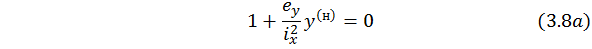
Обозначим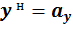 
– отрезок, который отсекает прямая по уравнению (3.8а), на главной (вертикальной) оси поперечного сечения, т.е. на оси у:
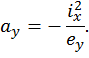
2) Пусть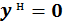 
, т.е. будем рассматривать точку, которая принадлежит оси х. Из уравнения (3.8) получим:
20
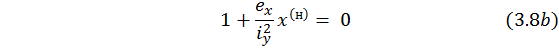
Обозначим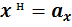 
– отрезок, который отсекает прямая по уравнению (3.8b), на главной (горизонтальной) оси поперечного сечения, т.е. на оси х:
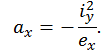
Таким образом, длины отрезков, которые НЛ отсекает на главных центральных осях поперечного сечения, находятся по формулам
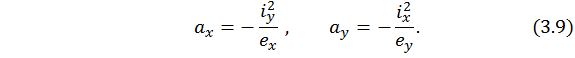
Здесь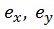 
–эксцентриситеты; 
, 
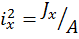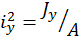– квадраты радиусов инерции сечения; 
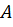– площадь поперечного сечения;
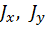– главные осевые моменты инерции сечения.
Положение нейтральной линии
На рис. 3.2 показано предположительное положение нейтральной линии в зависимости от положения полюса. Заметим, что полюс и нейтральная линия расположены по разные стороны от центра тяжести сечения; при этом нейтральная линия проходит через те четверти координатной плоскости, в которых составляющие нормальных напряжений имеют разные знаки.
Для каждой четверти координатной плоскости знаки напряжений от отдельного вида внутренних силовых факторов находятся в зависимости от положения полюса.
Напряжения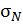 
от продольной силы во всех точках поперечного сечения отрицательны, так как заданная сила F является сжимающей.
21
Полюс расположен выше оси x, следовательно, при изгибе относительно оси x имеем сжатыми верхние волокна и, соответственно, на верхних волокнах (т.е. выше базиса) имеем напряжения сжатия (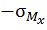 
).
Тогда, очевидно, ниже оси x волокна растянуты, существуют напряжения растяжения (+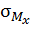 
). Аналогичные рассуждения проведем, рассматривая изгиб от заданной силы относительно оси 
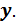Полюс расположен слева от оси у, следовательно, слева от оси у волокна сжаты, существуют напряжения сжатия ( 
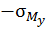); тогда справа от оси у волокна растянуты, существуют напряжения растяжения ( 
).
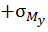Обратим внимание: так как знаки каждого слагаемого уже определены, все величины в правой части записанных выражений напряжений необходимо подставлять по модулю.
|
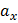
| С |
| x |
| 1 |
| 2 |
| О |
| Нейтральная линия |
| Рис. 3.2 |
|
|
|
|
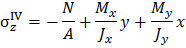
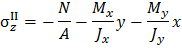
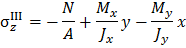
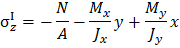
| y |
 |
Дата: 2019-02-25, просмотров: 312.
