Рассмотрим обобщенный график зависимости критических напряжений от гибкости 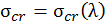 (рис. 5.5). В зависимости от гибкости можно выделить три категории стержней.
(рис. 5.5). В зависимости от гибкости можно выделить три категории стержней.
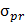
|
| С |
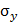
|
| λ0 |
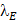
|
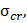 МПа
МПа
|
| Рис. 5.5 |
| l |
| А |
| В |
| АВ – прямая Тетмайера – Ясинского ВС – гипербола Эйлера |
1. Стержни малой гибкости 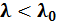 , имеющие постоянное значение критического напряжения:
, имеющие постоянное значение критического напряжения: 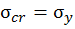 или
или 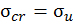 (
( 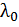 – значение гибкости, при которой критическое напряжение становится равным пределу текучести). Здесь
– значение гибкости, при которой критическое напряжение становится равным пределу текучести). Здесь 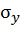 – предел текучести,
– предел текучести, 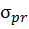 – предел пропорциональности (механические характеристики). Для таких стержней опасной является потеря прочности и расчет на устойчивость не проводят. Для разных марок сталей
– предел пропорциональности (механические характеристики). Для таких стержней опасной является потеря прочности и расчет на устойчивость не проводят. Для разных марок сталей 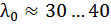 .
.
2. Стержни средней гибкости 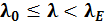 . В этом случае формула Эйлера неприемлема; используется подход Тетмайера – Ясинского: можно найти критическое напряжение
. В этом случае формула Эйлера неприемлема; используется подход Тетмайера – Ясинского: можно найти критическое напряжение 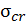 на основе достаточно простых зависимостей, полученных в результате обработки большого
на основе достаточно простых зависимостей, полученных в результате обработки большого
42
количества экспериментальных данных. Для различных материалов эта зависимость либо линейная, либо нелинейная. Например, для стали получена линейная зависимость в виде
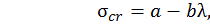 (5.22)
(5.22)
где 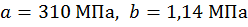 – эмпирические коэффициенты (сталь марки Ст3, предел пропорциональности
– эмпирические коэффициенты (сталь марки Ст3, предел пропорциональности 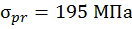 ). В этом же виде зависимость (5.22) можно использовать и для древесины, но эмпирические коэффициенты в этом случае другие:
). В этом же виде зависимость (5.22) можно использовать и для древесины, но эмпирические коэффициенты в этом случае другие: 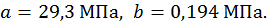
Людвиг Тетмайер (L.Tetmajer, 1850 –1905) – профессор Цюрихского политехнического института, установил предел применимости формулы Эйлера для стальных конструкций
Замечание. Для деревянных стержней (сосна, ель, лиственница) используется также формула в виде
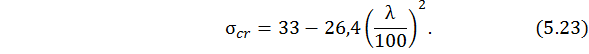
Заметим, что формула (5.25) дает меньшее значение критического напряжения по сравнению с результатом формулы (5.23) (при одном и том же значении гибкости), следовательно, обеспечивает в большей степени запас устойчивости стержней. Для чугуна ( 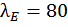 ) зависимость нелинейная
) зависимость нелинейная
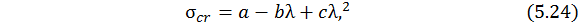
где 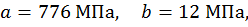
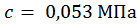 .
.
Важно. Зависимость Тетмайера – Ясинского можно применять при условии, что критические напряжения, вычисленные по эмпирическим формулам, не превосходят определенного предела. Для пластичных
43
материалов предельным является значение предела текучести 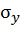 ; для хрупких материалов – значение предела прочности
; для хрупких материалов – значение предела прочности 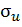 . После определения критического напряжения критическую силу находят по формуле
. После определения критического напряжения критическую силу находят по формуле
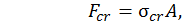 (5.25)
(5.25)
где 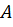 – площадь поперечного сечения брутто (доказано, что даже при больших местных ослаблениях сечений сжатого стержня их влияние на величину критической силы незначительно).
– площадь поперечного сечения брутто (доказано, что даже при больших местных ослаблениях сечений сжатого стержня их влияние на величину критической силы незначительно).
3. Стержни большой гибкости 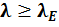 . Критическая сила определяется по формуле Эйлера (5.22). На основании формулы (5.17) очевидно, что графическим выражением зависимости
. Критическая сила определяется по формуле Эйлера (5.22). На основании формулы (5.17) очевидно, что графическим выражением зависимости 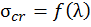 является гипербола, называемая гиперболой Эйлера (см. рис. 5.5).
является гипербола, называемая гиперболой Эйлера (см. рис. 5.5).
Таким образом, критические напряжения в зависимости от гибкости стержня вычисляют следующим образом:
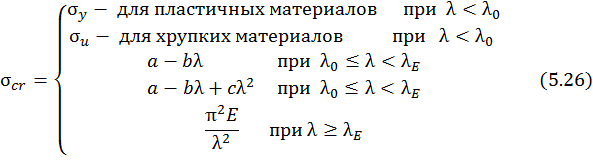
Практический расчет
центрально-сжатых стержней на устойчивость
В реальных условиях работы необходимо, чтобы сжатый стержень находился в устойчивом равновесии и имел определенный запас устойчивости. Это состояние обеспечивается в том случае, если действующая нагрузка меньше критического значения. Для обеспечения запаса устойчивости вводится коэффициент, уменьшающий расчетное
44
сопротивление на сжатие до значения, которое гарантирует устойчивость прямолинейной формы равновесия. Условие сохранения устойчивости имеет вид
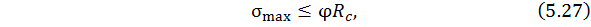
где 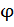 – коэффициент продольного изгиба (или коэффициент уменьшения основного расчетного сопротивления при продольном изгибе);
– коэффициент продольного изгиба (или коэффициент уменьшения основного расчетного сопротивления при продольном изгибе); 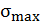 – максимальное расчетное нормальное напряжение. Коэффициент
– максимальное расчетное нормальное напряжение. Коэффициент 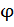 является функцией гибкости стержня, то есть
является функцией гибкости стержня, то есть 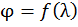 . Следовательно, он зависит от размеров и формы поперечного сечения стержня. Значения коэффициента продольного изгиба для различных
. Следовательно, он зависит от размеров и формы поперечного сечения стержня. Значения коэффициента продольного изгиба для различных
гибкостей разных материалов установлены СНиПами и обычно приводятся в виде таблиц (см., например, далее табл.5.1) или эмпирических формул. Например, для деревянных элементов
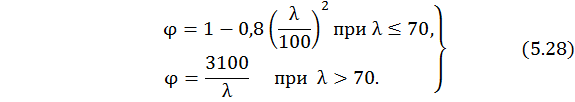
Обратимся вновь к условию (5.27). Как правило, его можно использовать для проверки устойчивости стержня, для выполнения проектировочного расчета и для определения допускаемой нагрузки.
Проверка устойчивости. Нормальные напряжения при центральном
сжатии определяются как 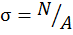 , тогда условие устойчивости с учетом равенства
, тогда условие устойчивости с учетом равенства 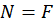 принимает вид
принимает вид
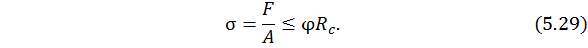
45
Проверка устойчивости выполняется непосредственно по формуле (5.29): все параметры заданы, значение коэффициента продольного изгиба 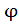 легко находится по таблице зависимости от гибкости стержня λ (вспомним, что гибкость находят на основе заданных геометрических параметров стержня).
легко находится по таблице зависимости от гибкости стержня λ (вспомним, что гибкость находят на основе заданных геометрических параметров стержня).
Проектировочный расчет обычно проводится как задача подбора поперечного сечения стержня. В этом случае условие (5.29) рассматривается в виде
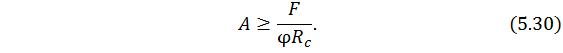
В записанном соотношении площадь поперечного сечения 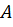 является неизвестной величиной; коэффициент продольного изгиба
является неизвестной величиной; коэффициент продольного изгиба 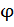 также неизвестен, так как параметры поперечного сечения не заданы и вычислить значение гибкости невозможно. Для решения задачи в этой
также неизвестен, так как параметры поперечного сечения не заданы и вычислить значение гибкости невозможно. Для решения задачи в этой
постановке используется метод последовательных приближений.
Дата: 2019-02-25, просмотров: 364.