В реальных условиях работы конструкция и ее отдельные элементы подвержены одновременному воздействию разных нагрузок, которые обуславливают возникновение в элементах конструкции сложной деформации или сложного сопротивления (последний термин употребляется чаще). Применительно к отдельному брусу можно утверждать, что сложное сопротивление – вид деформации, при котором в поперечных сечениях бруса возникает либо все шесть внутренних силовых факторов, либо одновременное сочетание нескольких (не менее двух). Важно отметить, что при рассмотрении сложного сопротивления принимается гипотеза о малости деформаций, то есть заведомо считается, что брус обладает достаточной жесткостью. Как следствие этого, справедлив принцип суперпозиции (наложения) внешних нагрузок.
Различают следующие виды сложного сопротивления.
● пространственный изгиб. Внутренними силовыми факторами являются 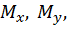
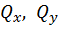 .
.
● пространственный изгиб с растяжением (или сжатием). Внутренними силовыми факторами являются 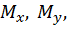
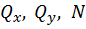 .
.
● пространственный изгиб с кручением. Внутренними силовыми факторами являются 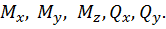
Рассмотрим частные случаи сложного сопротивления: косой изгиб как частный случай пространственного изгиба; внецентренное сжатие как частный случай пространственного изгиба со сжатием или растяжением; изгиб с кручением как частный случай пространственного изгиба с кручением.
9
Косой изгиб
Косой изгиб – вид деформации, при котором плоскость действия изгибающего момента не совпадает ни с одной из главных плоскостей бруса.
В сопротивлении материалов косой изгиб рассматривается как сочетание двух прямых поперечных изгибов: прямого изгиба в вертикальной плоскости (у z) и прямого изгиба в горизонтальной плоскости (xz). В этом случае внутренними силовыми факторами являются изгибающие моменты 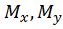 и поперечные силы
и поперечные силы 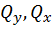 . При расчете на прочность поперечные силы не учитываются ввиду их незначительного влияния.
. При расчете на прочность поперечные силы не учитываются ввиду их незначительного влияния.
Рисунки 2.1 и 2.2 показывают разницу между прямым поперечным изгибом и косым изгибом. В первом случае (см. рис. 2.1, а) плоскость действия нагрузки и плоскость, содержащая главную центральную ось 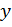 , совпадают; это особенно очевидно на рис. 2.1, б. На рис. 2.2 представлен тот же брус, но плоскость действия нагрузки не совпадает с плоскостью, содержащей ось
, совпадают; это особенно очевидно на рис. 2.1, б. На рис. 2.2 представлен тот же брус, но плоскость действия нагрузки не совпадает с плоскостью, содержащей ось 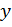 ; это показано на рис. 2.2, б.
; это показано на рис. 2.2, б.
| Рис. 2.1 |
| F |
| z |
| Силовая плоскость |
| a) |
| y |
| x |
| y |
| б) |
10
| Рис. 2.2 |
| a) |
| б) |
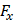
|
| y |
| x |
| Силовая плоскость |
| x |
| y |
| z |
| F |
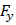
|
В любой 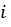 - й точке поперечного сечения возникают нормальные напряжения, которые определяются формулой
- й точке поперечного сечения возникают нормальные напряжения, которые определяются формулой
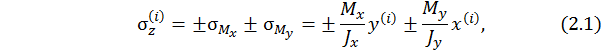
где x, y – координаты рассматриваемой 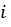 - й точки в системе главных центральных осей. В выражении (2.1) подразумевается, что все величины правой части берутся по модулю, а знак напряжения определяется знаком перед этим выражением. Фактически (2.1) рассматривается как
- й точки в системе главных центральных осей. В выражении (2.1) подразумевается, что все величины правой части берутся по модулю, а знак напряжения определяется знаком перед этим выражением. Фактически (2.1) рассматривается как
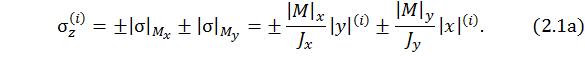
При рассмотрении косого изгиба расчет проводится в каждой из соответствующих плоскостей: в плоскости 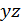 (вертикальная плоскость) и в плоскости
(вертикальная плоскость) и в плоскости 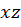 (горизонтальная плоскость). В каждой плоскости строятся эпюры изгибающего момента и поперечной силы от
(горизонтальная плоскость). В каждой плоскости строятся эпюры изгибающего момента и поперечной силы от
11
действия нагрузки именно в этой плоскости. Приняты обозначения эпюр: в вертикальной плоскости 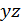 – эпюры
– эпюры 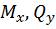 ; в горизонтальной плоскости
; в горизонтальной плоскости 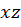 – эпюры
– эпюры 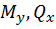 . (Построение эпюр при прямом поперечном изгибе рассматривается подробно в дисциплине «Техническая механика».)
. (Построение эпюр при прямом поперечном изгибе рассматривается подробно в дисциплине «Техническая механика».)
Практический интерес представляют опасные сечения бруса – сечения, в которых изгибающие моменты 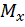 и
и 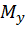 достигают наибольших по модулю значений. В большинстве расчетных случаев сечения, в которых возникают наибольшие изгибающие моменты
достигают наибольших по модулю значений. В большинстве расчетных случаев сечения, в которых возникают наибольшие изгибающие моменты 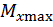 и
и 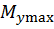 в соответствующих плоскостях, не совпадают по положению на оси бруса, то есть координаты z в этих сечениях разные. Поэтому опасным является сечение, в котором
в соответствующих плоскостях, не совпадают по положению на оси бруса, то есть координаты z в этих сечениях разные. Поэтому опасным является сечение, в котором 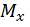 и
и 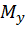 , хотя могут и не принимать одновременно наибольших значений, но в своей комбинации создают наиболее невыгодное сочетание.
, хотя могут и не принимать одновременно наибольших значений, но в своей комбинации создают наиболее невыгодное сочетание.
Дата: 2019-02-25, просмотров: 346.