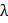● задают значение коэффициента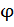 
на первом шаге вычисления;
● определяют площадь поперечного сечения по соотношению (5.30);
● вычисляют геометрические характеристики поперечного сечения;
● вычисляют гибкость стержня на основе полученного значения радиуса инерции поперечного сечения;
● находят расчетную величину коэффициента продольного изгиба, соответствующую вычисленной гибкости.
Анализ значений зависимости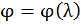 
(см. табл. 5.1) показывает, что 
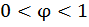. Как правило, в качестве первого приближения принимают 
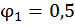или 
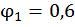. Если предполагаемое 
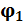и расчетное 
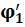значения не совпадают 
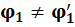, то полностью повторяют описанный выше расчет.
46
Таблица 5.1
Коэффициенты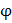 
продольного изгиба центрально-сжатых элементов
|
Гибкость | Значения | |||||||
| стали с расчетным сопротивлением R, МПа | древесины | |||||||
| 200 | 240 | 280 | 320 | 360 | 400 | 440 | ||
| 0 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 |
| 10 | 0,988 | 0,987 | 0,985 | 0,984 | 0,983 | 0,982 | 0,981 | 0,992 |
| 20 | 0,967 | 0,962 | 0,959 | 0,955 | 0,952 | 0,949 | 0,946 | 0,968 |
| 30 | 0,939 | 0,931 | 0,924 | 0,917 | 0,911 | 0,905 | 0,900 | 0,928 |
| 40 | 0,906 | 0,894 | 0,883 | 0,873 | 0,863 | 0,854 | 0,846 | 0,872 |
| 50 | 0,869 | 0,852 | 0,836 | 0,822 | 0,809 | 0,796 | 0,785 | 0,800 |
| 60 | 0,827 | 0,805 | 0,785 | 0,766 | 0,749 | 0,721 | 0,696 | 0,712 |
| 70 | 0,782 | 0,754 | 0,724 | 0,687 | 0,654 | 0,623 | 0,595 | 0,608 |
| 80 | 0,734 | 0,686 | 0,641 | 0,602 | 0,566 | 0,532 | 0,501 | 0,469 |
| 90 | 0,665 | 0,612 | 0,565 | 0,522 | 0,483 | 0,447 | 0,413 | 0,370 |
| 100 | 0,599 | 0,542 | 0,493 | 0,448 | 0,408 | 0,369 | 0,335 | 0,300 |
| 110 | 0,537 | 0,478 | 0,427 | 0,381 | 0,338 | 0,306 | 0,280 | 0,248 |
| 120 | 0,479 | 0,419 | 0,366 | 0,321 | 0,287 | 0,260 | 0,237 | 0,208 |
| 130 | 0,425 | 0,364 | 0,313 | 0,276 | 0,247 | 0,223 | 0,204 | 0,178 |
| 140 | 0,376 | 0,315 | 0,272 | 0,240 | 0,215 | 0,195 | 0,178 | 0,153 |
| 150 | 0,328 | 0,276 | 0,239 | 0,211 | 0,189 | 0,171 | 0,157 | 0,133 |
| 160 | 0,290 | 0,244 | 0,212 | 0,187 | 0,167 | 0,152 | 0,139 | 0,117 |
| 170 | 0,259 | 0,218 | 0,189 | 0,167 | 0,150 | 0,136 | 0,125 | 0,104 |
| 180 | 0,233 | 0,196 | 0,170 | 0,150 | 0,135 | 0,123 | 0,112 | 0,093 |
| 190 | 0,210 | 0,177 | 0,154 | 0,136 | 0,122 | 0,111 | 0,102 | 0,083 |
| 200 | 0,191 | 0,161 | 0,140 | 0,124 | 0,111 | 0,101 | 0,093 | 0,075 |
| 210 | 0,174 | 0,147 | 0,128 | 0,113 | 0,102 | 0,093 | 0,085 | 0,068 |
| 220 | 0,160 | 0,135 | 0,118 | 0,104 | 0,094 | 0,086 | 0,077 | 0,062 |
Примечания: 1. Для определения промежуточных значений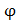 
допускается линейная интерполяция. 2. Для элементов из стали с расчетным сопротивлением 
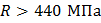коэффициент 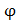следует определять по cпециальным формулам (см., напр, [3, с. 406]) или таблицам СНиП [4,5].
На втором шаге приближения принимают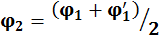 
, то
есть принимают среднее арифметическое значений первого приближения.
47
Расчет проводят до совпадений значений коэффициента продольного изгиба (предполагаемого и расчетного) с точностью до двух-трех десятичных знаков. Следует также сравнить значения нормальных напряжений (расчетного и предполагаемого) на определенном шаге приближения: расчет прекращают, если разница между указанными напряжениями не превышает 2÷5 %.
Имеем:
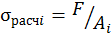– расчетное напряжение, соответствующее i -му приближению; 
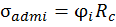– предполагаемое напряжение.
Погрешность вычисления на i-м шаге приближения вычисляется как соотношение:
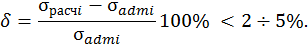
Значение площади поперечного сечения принимают равным значению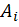 
, полученному на последнем расчетном шаге приближения.
Таким образом, при расчете на устойчивость должно выполняться услови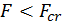е 
, где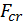 
– критическая сила. Как правило, принимают
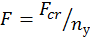, где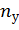 
– нормативный коэффициент устойчивости, зависящий в основном от назначения стержней и его материала. Для стальных стержней и стальных конструкций 
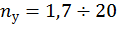; для элементов машиностроительных конструкций 
.
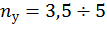48
Глава 6
РАСЧЕТ СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫХ
БАЛОК И РАМ МЕТОДОМ СИЛ
Понятие статически неопределимой
Стержневой системы
Статически неопределимой стержневой системой называют систему, которая не может быть рассчитана с использованием только уравнений равновесия – уравнений статики. В такой системе существуют лишние с точки зрения уравнений статики связи. В дальнейшем будем рассматривать стержневые статически неопределимые системы.
Условно можно выделить два вида статической неопределимости:
1) внешняя неопределимость – наблюдается в статически неопределимых системах, в которых существуют лишние опорные закрепления. В этом случае из уравнений статики нельзя найти все опорные реакции.
2) внутренняя неопределимость – наблюдается в системах с лишними связями, введенными для взаимного соединения частей системы. В этом случае из уравнений равновесия нельзя найти все внутренние силовые факторы.
Существуют различные методы расчета статически неопределимых систем. Важнейшими из них являются: метод сил, метод перемещений, смешанный метод и др. (Эти методы подробно рассматриваются в дисциплине «Строительная механика».) Здесь же рассмотрим более подробно расчет статически неопределимых систем методом сил на действие неподвижной нагрузки. Название метода подсказывает, что за неизвестные при использовании этого метода приняты силы – фактические усилия в лишних связях. Именно для неизвестных сил будут рассматриваться определенные уравнения. Но расчет начинается с определения степени статической неопределимости.
49
Основной характеристикой статически неопределимых систем является степень статической неопределимости – количество «лишних» связей, которые необходимо мысленно удалить из статически неопределимой системы для преобразования ее в статически определимую. Заметим, что слово «лишние» заключено в кавычки не случайно: некоторые связи являются лишними с точки зрения уравнений статики (их количество является недостаточным). На практике статически неопределимые системы являются более жесткими системами по сравнению с системами статически определимыми.
Степень статической неопределимости n для плоских систем находится по различным формулам. Наиболее простой является следующая формула:
1) 
.
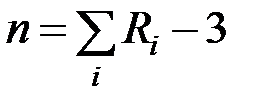Здесь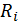 
- количество опорных реакций в системе, суммирование проводится по количеству реакций. Число «3» указывает, что для плоского случая существуют три уравнения равновесия – три уравнений статики. Но эта формула неприменима для систем, имеющих замкнутые контуры. Для них применяется формула в виде:
2) 
,
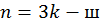где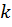 
– число замкнутых контуров, включая опорные, которые можно образовать в системе; ш – общая кратность всех шарниров. Кратность шарнира – величина, на единицу меньшая количества соединяемых шарниром стержней. На рис. 6.1 показаны примеры вычисления кратности. Значение кратности показано цифрой рядом с шарниром.
| 1 |
| 2 |
| 3 |
Рис. 6.1
Вычисление степени статической неопределимости проиллюстрируем примерами, показанными на рис. 6.2. Обратим внимание на
50
вычисление степени статической неопределимости на рис. 6.2, б: из общего количества реакций (в каждой жесткой заделке существует по три реакции) вычитается число 4 (а не 3, как в формуле). В этом случае к количеству уравнений равновесия на плоскости добавляется уравнение равновесия в виде суммы изгибающих моментов относительно шарнира самой системы. Кратность шарнира в примере равна единице, поэтому добавлено одно уравнение. В примерах рис. 6.2, в и г степень статической неопределимости вычисляется через замкнутые контуры (римскими цифрами пронумерованы замкнутые контуры, уже существующие или образованные).
а) б)
|
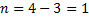
| 1 |
|
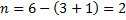
| 2 |
| 1 |
| 1 |
| 2 |
| I |
| IIII |
| IIIII |
|
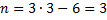
| 1 |
| 1 |
| I |
| II |
| 1 |
| 1 |
|
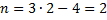
Рис. 6.2
51
Дата: 2019-02-25, просмотров: 333.
