В зависимости от положения нейтральной линии
1) Рассмотрим случай, когда нейтральная линия не проходит через поперечное сечение.
Предположим, что сила приложена в центре тяжести поперечного сечения, значит, полюс находится в центре тяжести поперечного сечения. В этом случае нормальные напряжения в поперечном сечении распределены равномерно и имеют один знак; имеем осевое (центральное) сжатие (растяжение).
26
Тогда 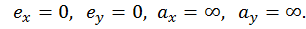 (Обратим внимание: при минимальных значениях эксцентриситетов имеем максимальные значения отрезков, которые НЛ отсекает на главных центральных осях.)
(Обратим внимание: при минимальных значениях эксцентриситетов имеем максимальные значения отрезков, которые НЛ отсекает на главных центральных осях.)
2) Увеличим эксцентриситеты, т.е. полюс будем отдалять от центра тяжести поперечного сечения. В этом случае отрезки будут уменьшаться (в силу обратно пропорциональной зависимости между эксцентриситетами и отрезками): НЛ будет приближаться к поперечному сечению. При некотором положении НЛ может коснуться поперечного сечения. Очевидно, в месте касания нормальные напряжения равны нулю.
Утверждение. Если НЛ касается контура поперечного сечения, то сжимающая (растягивающая) сила приложена в границе ядра сечения.
3) Рассмотрим случай, когда НЛ пересекает поперечное сечение. В поперечном сечении возникают нормальные напряжения разных знаков. В произвольной точке поперечного сечения нормальное напряжение имеет вид:
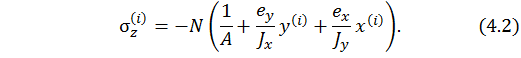
Предположим, что произвольная точка принадлежит нейтральной линии, тогда уравнение НЛ запишем в виде:
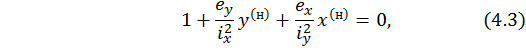
где 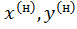 – координаты рассматриваемой точки.
– координаты рассматриваемой точки.
Выполним анализ рисунка, представленного далее (см. рис.4.3).
1) Пусть точка О – полюс, а точка i расположена на НЛ. (НЛ на рисунке – линия а-а).
2) Поменяем местами эти точки. Предположим, что сжимающая сила приложена в точке i ( точка i – полюс), а точка О принадлежит НЛ, поэтому 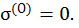
27
| a |
| i • |
| c |
| i |
| i |
| O |
| a |
| x |
| НЛ |
| x |
| y |
Рис. 4.3
3) Рассмотрим любую другую точку, принадлежащую прямой а-а. Предположим, что именно эта (любая) точка есть полюс. В этой точке 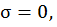 значит, НЛ снова пройдет через точку О, но не будет совпадать с предыдущей НЛ.
значит, НЛ снова пройдет через точку О, но не будет совпадать с предыдущей НЛ.
Замечания. 1) При любом положении полюса на прямой а-а НЛ будет проходить через точку О.
2) Каждому положению полюса соответствует определенная НЛ.
3) Разным положениям полюса на прямой а-а соответствуют разные нулевые линии, но все они проходят через точку О.
Выводы: 1) При перемещении полюса вдоль некоторой прямой а-а нулевые линии вращаются вокруг точки О.
2) При повороте НЛ вокруг некоторой фиксированной точки контура сечения точка приложения силы перемещается вдоль некоторой прямой.
Построение ядра сечения
Построение ядра сечения основывается на свойстве нейтральной линии: если нейтральная линия совпадает с контуром поперечного сечения, то полюс находится на контуре ядра сечения.
28
Таким образом, для построения ядра сечения необходимо задать положения нейтральной линии в виде касательных к контуру поперечного сечения. При каждом конкретном положении нейтральной линии известными являются величины отрезков, которые нейтральная линия отсекает на координатных осях: 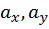 . Тогда координаты полюса находим из выражений:
. Тогда координаты полюса находим из выражений:
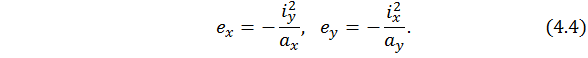
Дата: 2019-02-25, просмотров: 358.