Важно подчеркнуть, что выбранная основная система метода сил (ОСМС) должна быть системой статически определимой и должна соответствовать основным требованиям правильного образования существующих стержневых систем. Последние называют «Правила образования геометрически неизменяемых систем» и подробно рассматривают в дисциплине «Строительная механика».

53

Если можно образовать разные виды ОСМС, то выбирают ту систему, в которой строить различные эпюры проще.

Продолжим рассмотрение с исследования выбранной ранее ОСМС. На основании принципа независимости действия сил вертикальное перемещение точки А можно рассматривать в виде суммарных вертикальных перемещений этой точки от отдельного действия каждого вида нагрузки. Можно записать:

,

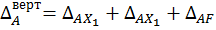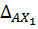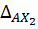где  и – вертикальные перемещения точки А от отдельного действия  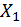и 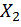 соответственно;  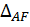– вертикальное перемещение точки от заданного силового воздействия. ( Индексом  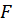здесь и в дальнейшем принято обозначать любое силовое воздействие в виде сосредоточенных сил или моментов, в виде равномерно распределенной нагрузки.) Аналогично можно записать вертикальное перемещение точки В:

.

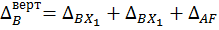Очевидно, по условию в точках А и В отсутствуют вертикальные перемещения, так как в этих точках расположены вертикально шарнирно подвижные опоры. Но в выбранной основной системе вертикальные перемещения в точках А и В существуют: указанные точки свободны от закреплений. Следовательно, для устранения полученного противоречия между заданной и основной системами необходимо принять вертикальные перемещения в точках А и В равными нулю. Таким образом, заставляя выбранную ОСМС работать как заданную, получим систему уравнений:

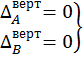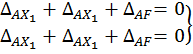    или                        (6.1)

54

Обратим внимание: все перемещения левой части уравнений (6.1) должны быть вычислены по эпюрам, построенным в основной системе от соответствующих единичных воздействий и заданной нагрузки.

Для линейно деформируемых упругих систем любое перемещение ∆, вызванное силам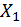и и 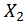, можно представить в виде произведения силы на перемещение, найденное от единичного воздействия:

 .

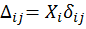Здесь 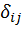– перемещение 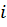- точки по направлению силы 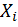, вызванное силой 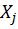=1; в нашем случае 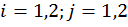. Тогда в левой части уравнений (6.1) соответствующие слагаемые можно записать в виде:

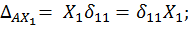
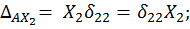
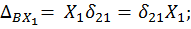
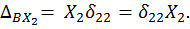
С учетом записанных соотношений система (6.1) принимает окончательный вид:

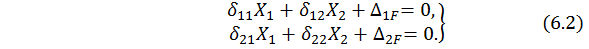
Полученная система (6.2) представляет собой систему канонических уравнений метода сил для дважды статически неопределимой системы (степень статической неопределимости 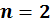) .  Для рамы (или любой стержневой системы) n раз статически неопределимой канонические уравнения метода сил принимают вид

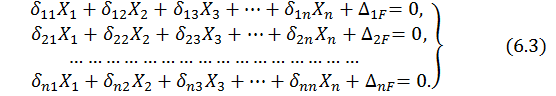
55

Смысл канонических уравнений: все перемещения в направлении отброшенных связей (обобщенные перемещения) от всех неизвестных и заданной нагрузки равны нулю. Каждое уравнение системы выражает условие равенства нулю перемещения по направлению соответствующего неизвестного.