Расчет на прочность выполняется в опасных точках поперечного сечения. Опасными являются точки, наиболее удаленные от нейтральной линии. Нейтральная линия – линия нулевых напряжений, следовательно, на нейтральной линии нормальное напряжение в произвольной точке равно нулю. Получим уравнение нейтральной линии при косом изгибе.
Предположим, что точка i принадлежит нейтральной линии. Тогда нормальное напряжение в этой точке по выражению (2.1) приравняем нулю:
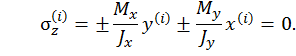
Рассмотрим последнее выражение с положительными знаками, представим его в виде:
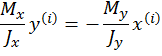
12
Выделим из предыдущего равенства отношение координат. Получим
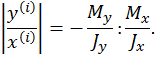
Очевидно, в левой части записанного равенства имеем выражение тангенса некоторого угла. Окончательно запишем выражение в виде
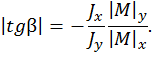
В учебной литературе часто вводится некоторый острый угол 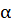 , для которого
, для которого
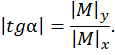
В этом случае можно считать, что 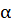 – угол, определяющий силовую линию (отсчитывается от горизонтальной главной центральной оси). Тогда можно записать
– угол, определяющий силовую линию (отсчитывается от горизонтальной главной центральной оси). Тогда можно записать
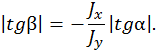
Замечание относительно знака. Полученный знак минус соответствует исходному предположению о положительных знаках в выражении (2.1). Очевидно, при предположении отрицательных знаков нами был бы получен знак плюс.
Вывод. Нейтральная линия в случае косого изгиба проходит через центр тяжести поперечного сечения и составляет угол b с горизонтальной центральной осью сечения. Угол b находим из соотношения
13
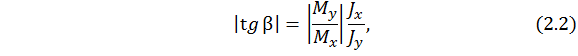
где 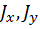 – главные центральные осевые моменты инерции сечения.
– главные центральные осевые моменты инерции сечения.
Представленная запись формулы в виде (2.2) позволяет найти значение угла b (при правильном вычислении угол b – острый) по модулю. Естественно, возникает вопрос, а как правильно отложить этот угол от горизонтальной оси: по ходу часовой стрелки или против хода часовой стрелки? Для проведения нейтральной линии предлагается следующий подход. Так как нейтральная линия – это линия нулевых напряжений, очевидно, что она пройдет через те четверти координатной плоскости, в которых сочетание значений напряжений от изгиба в разных плоскостях может дать суммарное нулевое значение. Это возможно в тех четвертях координатной плоскости, в которых напряжения имеют разные знаки.
Определим знаки нормальных напряжений, возникающих в опасном сечении бруса от изгиба в разных плоскостях. Предположим: в опасном 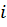 - м сечении бруса
- м сечении бруса 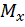 растягивает нижние относительно оси x волокна, а
растягивает нижние относительно оси x волокна, а 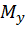 растягивает правые относительно оси у волокна. Так как эпюры изгибающих моментов строятся на растянутых волокнах, то там, где волокна растянуты, имеем напряжение растяжения, то есть положительное по знаку нормальное напряжение.
растягивает правые относительно оси у волокна. Так как эпюры изгибающих моментов строятся на растянутых волокнах, то там, где волокна растянуты, имеем напряжение растяжения, то есть положительное по знаку нормальное напряжение.
На рис. 2.3 показано распределение знаков нормальных напряжений в каждой четверти координатной плоскости, соответствующее данному предположению о действии изгибающих моментов (оси у, x – главные центральные оси сечения). Верхний индекс (показан римской цифрой) нормальных напряжений соответствует номеру четверти координатной плоскости. Вспомним из математики: первой обозначают координатную четверть (или еще называют квадрант), в которой координаты любой точки положительны. Координатные четверти нумеруют против хода часовой стрелки. В рассматриваемом примере нейтральная линия проходит через 1-ую и 3-ю четверти координатной плоскости поперечного сечения, то есть там, где имеем разные знаки
14
слагаемых напряжения. Только в этих четвертях алгебраическая сумма нормальных напряжений может быть равной нулю.
Угол b при сделанных предположениях относительно растягивающих волокон откладывается от горизонтальной оси x против хода часовой стрелки (см. рис. 2.3).
| Нейтральная линия |
| 1 |
| 2 |
| b |
| y |
| С |
| x |
| Рис. 2.3 |
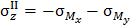
|
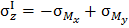
|
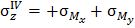
|
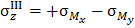
|
Дата: 2019-02-25, просмотров: 524.