Столетовых»
(ВлГУ)
С. А. МАВРИНА
НЕКОТОРЫЕ ВОПРОСЫ ТЕОРИИ СОПРОТИВЛЕНИЯ МАТЕРИАЛОВ
ЛЕКЦИОННЫЙ КУРС ДЛЯ ВЫПОЛНЕНИЯ РАСЧЕТНО-ГРАФИЧЕСКИХ РАБОТ
2018
УДК 539.3
ББК 30.121
Рецензент
Кандидат технических наук,
доцент кафедры «Строительное производство»
С. В. Прохоров
Некоторые вопросы теории сопротивления материалов. Лекционный курс для выполнения расчетно-графических работ: Учебное электронное издание / Владим. гос. ун-т; сост. С. А. Маврина. – Владимир, 2018. – 62 с.
Содержатся теоретические основы сложного сопротивления, устойчивости и расчета статически неопределимых систем методом сил в сопротивлении материалов.
Предназначены для студентов, обучающихся по направлению «Строительство». Ориентировано для студентов очной, заочной и заочной с элементами дистанционных технологий форм обучения.
Табл. 1. Ил. 22. Библиогр.: 6 назв.
УДК 539.3
ББК 30.121
Глава 1. ОСНОВНЫЕ ПОНЯТИЯ
Введение
«Сопротивление материалов» – раздел механики твердого деформируемого тела, в котором изучается поведение различных тел под нагрузкой. В общепринятом смысле сопротивление материалов рассматривается как наука об инженерных методах расчета на прочность, жесткость и устойчивость отдельных элементов конструкций и простых систем. В курсе сопротивления материалов решаются три основные задачи:
● изложение методов расчета элементов конструкций на прочность.
● изложение методов расчета элементов конструкций на жесткость.
●изложение методов расчета элементов конструкций на устойчивость.
Решение указанных задач в сопротивлении материалов основано на использовании ряда гипотез и допущений, схематизации реальных тел и нагрузок.
Схематизация опорных устройств
В сопротивлении материалов широко распространенным объектом исследования является балка – стержень, нагруженный силами, действующими в направлении его поперечной оси. Как правило, балки рассматриваются прикрепленными к земле с помощью опорных устройств или опор. На рис. 1.3 показаны наиболее распространенные типы опор в виде шарнирно-подвижной, шарнирно-неподвижной опор и жесткой заделки. От действия внешней нагрузки в опорах возникают опорные реакции, которые (после их нахождения) учитываются наравне с заданной нагрузкой.
7
| или |
| или |
| Рис. 1.3 |
| или |
| Жесткая заделка |
| Шарнирно-неподвижная опора (возможные варианты изображения) |
| Шарнирно-подвижная опора |
Понятие о расчетной схеме
При решении конкретных задач методами сопротивления материалов реальные тела под заданной нагрузкой заменяются расчетной схемой.
Расчетная схема – упрощенное изображение реального объекта с обязательным привнесением конкретных параметров этого объекта.
К этим параметрам прежде всего относят реальные размеры, форму и размеры поперечного сечения, материал (для того, чтобы правильно учитывать физические характеристики именно этого материала). Расчетная схема, во многом, выбирается интуитивно, однако в основе выбора лежат рассмотренные в §§ 1.2-1.4 правила схематизации элементов, внешних воздействий и опорных устройств.
8
Глава 2. СЛОЖНОЕ СОПРОТИВЛЕНИЕ: КОСОЙ ИЗГИБ
Косой изгиб
Косой изгиб – вид деформации, при котором плоскость действия изгибающего момента не совпадает ни с одной из главных плоскостей бруса.
В сопротивлении материалов косой изгиб рассматривается как сочетание двух прямых поперечных изгибов: прямого изгиба в вертикальной плоскости (у z) и прямого изгиба в горизонтальной плоскости (xz). В этом случае внутренними силовыми факторами являются изгибающие моменты 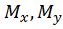 и поперечные силы
и поперечные силы 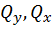 . При расчете на прочность поперечные силы не учитываются ввиду их незначительного влияния.
. При расчете на прочность поперечные силы не учитываются ввиду их незначительного влияния.
Рисунки 2.1 и 2.2 показывают разницу между прямым поперечным изгибом и косым изгибом. В первом случае (см. рис. 2.1, а) плоскость действия нагрузки и плоскость, содержащая главную центральную ось 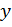 , совпадают; это особенно очевидно на рис. 2.1, б. На рис. 2.2 представлен тот же брус, но плоскость действия нагрузки не совпадает с плоскостью, содержащей ось
, совпадают; это особенно очевидно на рис. 2.1, б. На рис. 2.2 представлен тот же брус, но плоскость действия нагрузки не совпадает с плоскостью, содержащей ось 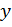 ; это показано на рис. 2.2, б.
; это показано на рис. 2.2, б.
| Рис. 2.1 |
| F |
| z |
| Силовая плоскость |
| a) |
| y |
| x |
| y |
| б) |
10
| Рис. 2.2 |
| a) |
| б) |
|
| y |
| x |
| Силовая плоскость |
| x |
| y |
| z |
| F |
|
В любой 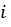 - й точке поперечного сечения возникают нормальные напряжения, которые определяются формулой
- й точке поперечного сечения возникают нормальные напряжения, которые определяются формулой
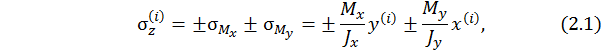
где x, y – координаты рассматриваемой 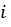 - й точки в системе главных центральных осей. В выражении (2.1) подразумевается, что все величины правой части берутся по модулю, а знак напряжения определяется знаком перед этим выражением. Фактически (2.1) рассматривается как
- й точки в системе главных центральных осей. В выражении (2.1) подразумевается, что все величины правой части берутся по модулю, а знак напряжения определяется знаком перед этим выражением. Фактически (2.1) рассматривается как
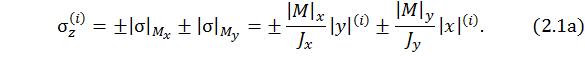
При рассмотрении косого изгиба расчет проводится в каждой из соответствующих плоскостей: в плоскости 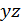 (вертикальная плоскость) и в плоскости
(вертикальная плоскость) и в плоскости 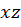 (горизонтальная плоскость). В каждой плоскости строятся эпюры изгибающего момента и поперечной силы от
(горизонтальная плоскость). В каждой плоскости строятся эпюры изгибающего момента и поперечной силы от
11
действия нагрузки именно в этой плоскости. Приняты обозначения эпюр: в вертикальной плоскости 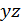 – эпюры
– эпюры 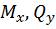 ; в горизонтальной плоскости
; в горизонтальной плоскости 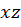 – эпюры
– эпюры 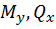 . (Построение эпюр при прямом поперечном изгибе рассматривается подробно в дисциплине «Техническая механика».)
. (Построение эпюр при прямом поперечном изгибе рассматривается подробно в дисциплине «Техническая механика».)
Практический интерес представляют опасные сечения бруса – сечения, в которых изгибающие моменты 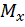 и
и 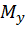 достигают наибольших по модулю значений. В большинстве расчетных случаев сечения, в которых возникают наибольшие изгибающие моменты
достигают наибольших по модулю значений. В большинстве расчетных случаев сечения, в которых возникают наибольшие изгибающие моменты 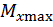 и
и 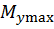 в соответствующих плоскостях, не совпадают по положению на оси бруса, то есть координаты z в этих сечениях разные. Поэтому опасным является сечение, в котором
в соответствующих плоскостях, не совпадают по положению на оси бруса, то есть координаты z в этих сечениях разные. Поэтому опасным является сечение, в котором 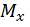 и
и 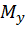 , хотя могут и не принимать одновременно наибольших значений, но в своей комбинации создают наиболее невыгодное сочетание.
, хотя могут и не принимать одновременно наибольших значений, но в своей комбинации создают наиболее невыгодное сочетание.
Сжатии (растяжении)
Расчет на прочность проводится в опасных точках поперечного сечения. Поэтому практический интерес представляют именно эти точки. Как и при косом изгибе, опасными являются точки, наиболее удаленные от нейтральной линии.
При внецентренном сжатии (растяжении) нейтральная линия не проходит через центр тяжести поперечного сечения, а отсекает на главных центральных осях отрезки 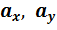 .
.
Определим длины отрезков, которые отсекает нейтральная линия в поперечном сечении.
Первоначально введем понятие новых для нас геометрических характеристик.
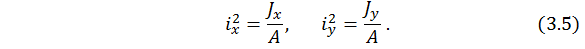
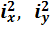 – квадраты радиусов инерции поперечного сечения.
– квадраты радиусов инерции поперечного сечения.
Выражение (3.4) перепишем с учетом (3.5). При этом второе и третье слагаемое умножим и разделим одновременно на параметр площади поперечного сечения A.
19
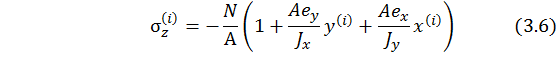
Далее в записи (3.6) вынесем общий множитель, окончательно получим выражение нормальных напряжений в виде
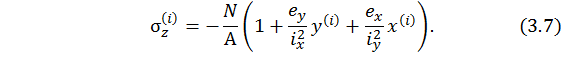
Пусть некоторая произвольная точка принадлежит нейтральной линии. Обозначим ее координаты 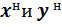 . Подставим эти координаты в равенство (3.7) и приравняем его нулю. Тогда получим уравнение нейтральной линии в виде
. Подставим эти координаты в равенство (3.7) и приравняем его нулю. Тогда получим уравнение нейтральной линии в виде
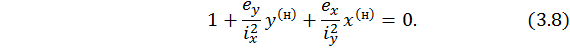
По уравнению (3.8) можно определить отрезки, которые НЛ отсекает на главных центральных осях поперечного сечения.
1) Пусть 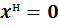 , т.е. будем рассматривать точку, которая принадлежит оси у. Из уравнения (8) получим:
, т.е. будем рассматривать точку, которая принадлежит оси у. Из уравнения (8) получим:
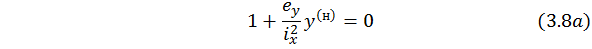
Обозначим 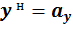 – отрезок, который отсекает прямая по уравнению (3.8а), на главной (вертикальной) оси поперечного сечения, т.е. на оси у:
– отрезок, который отсекает прямая по уравнению (3.8а), на главной (вертикальной) оси поперечного сечения, т.е. на оси у:
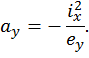
2) Пусть 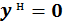 , т.е. будем рассматривать точку, которая принадлежит оси х. Из уравнения (3.8) получим:
, т.е. будем рассматривать точку, которая принадлежит оси х. Из уравнения (3.8) получим:
20
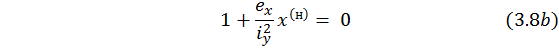
Обозначим 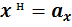 – отрезок, который отсекает прямая по уравнению (3.8b), на главной (горизонтальной) оси поперечного сечения, т.е. на оси х:
– отрезок, который отсекает прямая по уравнению (3.8b), на главной (горизонтальной) оси поперечного сечения, т.е. на оси х:
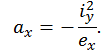
Таким образом, длины отрезков, которые НЛ отсекает на главных центральных осях поперечного сечения, находятся по формулам
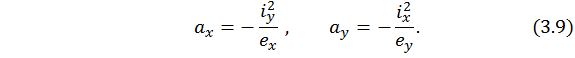
Здесь 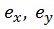 –эксцентриситеты;
–эксцентриситеты; 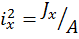 ,
, 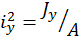 – квадраты радиусов инерции сечения;
– квадраты радиусов инерции сечения; 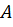 – площадь поперечного сечения;
– площадь поперечного сечения;
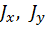 – главные осевые моменты инерции сечения.
– главные осевые моменты инерции сечения.
Положение нейтральной линии
На рис. 3.2 показано предположительное положение нейтральной линии в зависимости от положения полюса. Заметим, что полюс и нейтральная линия расположены по разные стороны от центра тяжести сечения; при этом нейтральная линия проходит через те четверти координатной плоскости, в которых составляющие нормальных напряжений имеют разные знаки.
Для каждой четверти координатной плоскости знаки напряжений от отдельного вида внутренних силовых факторов находятся в зависимости от положения полюса.
Напряжения 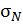 от продольной силы во всех точках поперечного сечения отрицательны, так как заданная сила F является сжимающей.
от продольной силы во всех точках поперечного сечения отрицательны, так как заданная сила F является сжимающей.
21
Полюс расположен выше оси x, следовательно, при изгибе относительно оси x имеем сжатыми верхние волокна и, соответственно, на верхних волокнах (т.е. выше базиса) имеем напряжения сжатия ( 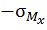 ).
).
Тогда, очевидно, ниже оси x волокна растянуты, существуют напряжения растяжения (+ 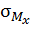 ). Аналогичные рассуждения проведем, рассматривая изгиб от заданной силы относительно оси
). Аналогичные рассуждения проведем, рассматривая изгиб от заданной силы относительно оси 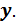 Полюс расположен слева от оси у, следовательно, слева от оси у волокна сжаты, существуют напряжения сжатия (
Полюс расположен слева от оси у, следовательно, слева от оси у волокна сжаты, существуют напряжения сжатия ( 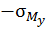 ); тогда справа от оси у волокна растянуты, существуют напряжения растяжения (
); тогда справа от оси у волокна растянуты, существуют напряжения растяжения ( 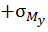 ).
).
Обратим внимание: так как знаки каждого слагаемого уже определены, все величины в правой части записанных выражений напряжений необходимо подставлять по модулю.
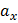
|
| С |
| x |
| 1 |
| 2 |
| О |
| Нейтральная линия |
| Рис. 3.2 |
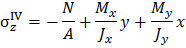
|
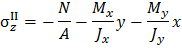
|
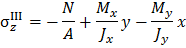
|
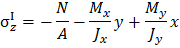
|
| y |
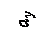 |
Глава 4. ЯДРО СЕЧЕНИЯ
Определение ядра сечения
Ядро сечения – выпуклая область вокруг центра тяжести сечения, обладающая свойством: если действующая сила приложена в ядре сечения, то нормальные напряжения во всех точках поперечного сечения имеют одинаковый знак. Знак нормальных напряжений определяется направлением действующей силы: если сила сжимающая, то напряжения отрицательные; если сила растягивающая, то напряжения положительные.
Известно, что многие строительные материалы (бетон, кирпич) плохо работают на растяжение, но хорошо выдерживают сжимающие нагрузки: 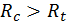 в несколько раз. Поэтому на практике ставится задача не допустить появления растягивающих напряжений в колоннах, выполненных из хрупких материалов. Этой задаче и служит построения ядра сечения в плоскости поперечного сечения.
в несколько раз. Поэтому на практике ставится задача не допустить появления растягивающих напряжений в колоннах, выполненных из хрупких материалов. Этой задаче и служит построения ядра сечения в плоскости поперечного сечения.
24
Свойства ядра сечения
1) Чем дальше от начала координат расположен полюс, т.е. чем больше по абсолютной величине эксцентриситеты 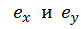 , тем ближе к центру тяжести проходит нейтральная линия. Это очевидно: с увеличением эксцентриситетов уменьшаются длины отрезков, которые нейтральная линия (НЛ) отсекает на главных центральных осях поперечного сечения, и наоборот.
, тем ближе к центру тяжести проходит нейтральная линия. Это очевидно: с увеличением эксцентриситетов уменьшаются длины отрезков, которые нейтральная линия (НЛ) отсекает на главных центральных осях поперечного сечения, и наоборот.
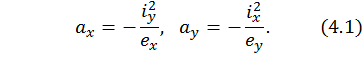
2) Если полюс расположен на одной из главных центральных осей инерции, то НЛ перпендикулярна этой оси. Докажем это.
| Рис. 4.1 |
| О |
| y |
| x |
| НЛ |
1-е положение. Пусть точка О находится на горизонтальной оси х. Очевидно, существует 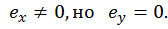 Тогда
Тогда
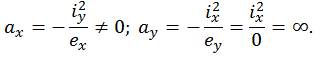
25
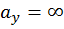 означает, что пересечение НЛ с осью у возможно только в бесконечности, т. е. НЛ параллельна вертикальной оси у.
означает, что пересечение НЛ с осью у возможно только в бесконечности, т. е. НЛ параллельна вертикальной оси у.
2-е положение. Пусть точка О находится на вертикальной оси у. Очевидно, существует 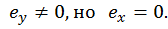 Тогда
Тогда
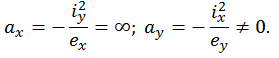
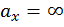 означает, что пересечение НЛ с осью x возможно только в бесконечности, т. е. НЛ параллельна горизонтальной оси x .
означает, что пересечение НЛ с осью x возможно только в бесконечности, т. е. НЛ параллельна горизонтальной оси x .
| y |
| О |
| x |
| НЛ |
Рис. 4.2
Построение ядра сечения
Построение ядра сечения основывается на свойстве нейтральной линии: если нейтральная линия совпадает с контуром поперечного сечения, то полюс находится на контуре ядра сечения.
28
Таким образом, для построения ядра сечения необходимо задать положения нейтральной линии в виде касательных к контуру поперечного сечения. При каждом конкретном положении нейтральной линии известными являются величины отрезков, которые нейтральная линия отсекает на координатных осях: 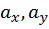 . Тогда координаты полюса находим из выражений:
. Тогда координаты полюса находим из выражений:
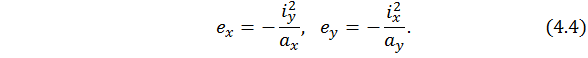
Основные понятия
При сжатии стержня может наблюдаться не только потеря прочности, но и потеря устойчивости (выпучивание стержня). При этом несущая способность стержня вследствие потери устойчивости может быть исчерпана раньше, чем непосредственно от сжатия.
Проблема (задача) потери устойчивости возникает при осевом (центральном) сжатии гибкого достаточно длинного и тонкого стержня. Вспомним, что при осевом сжатии короткого стержня наблюдается деформация сжатия. Из теоретической механики известно, что равновесие твердых тел может быть устойчивым и неустойчивым. Упругое равновесие называется устойчивым, если при каком-либо внешнем воздействии система стремится вернуться в исходное положение. В случае неустойчивого равновесия система деформируется до полного разрушения. Замечание. В нашем курсе мы будем рассматривать потерю устойчивости отдельных стержней системы, а не потерю устойчивости системы стержней в целом.
Потерей устойчивости стержня называется его переход из первоначального положения равновесия к другому положению равновесия, то есть переход из одной равновесной формы в другую. Нагрузка, при которой происходит потеря устойчивости, называется критической. На рис. 5.1 показаны возможные положения стержня в зависимости от значения сжимающей силы. Обозначим 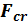 – некоторое критическое значение сжимающей силы.
– некоторое критическое значение сжимающей силы.
Критической силой принято называть наименьшее значение центрально приложенной силы, при котором прямолинейная форма равновесия становится неустойчивой. Для ответа на вопрос о состоянии стержня или стержневой системы с точки зрения потери устойчивости действующее значение сжимающей силы сравнивается с с критическим значением.
32
| F = F cr |
| б) |
| F < F cr |
| а) |
| F > F cr |
| в) |
| Рис. 5.1 |
Очевидно, стержень находится в состоянии устойчивого равновесия, если действующая сжимающая сила меньше некоторого критического значения 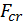 – рис. 5.1, а.
– рис. 5.1, а.
Если сжимающая сила достигает критического значения, стержень отклоняется от вертикального положения; возникает состояние как бы безразличного равновесия: после отклонения стержень приобретает равновесие и в искривленном положении; при этом он не возвращается в первоначальное положение, но и не искривляется далее. Происходит бифуркация, то есть раздвоение состояния равновесия: прямолинейная форма теряет устойчивость, а криволинейная еще не успевает ее приобрести (см. рис. 5.1, б). Наконец, если действующая сила превышает критическое значение, то возникает новая криволинейная форма устойчивого равновесия (см. рис. 5.1, в). С практической точки зрения состояния, изображенные на рис. 5.1, б и 5.1, в, для строительных конструкций неприемлемы. Например, в последнем случае стержень работает не только на сжатие, но и дополнительно на изгиб: могут возникнуть недопустимо большие прогибы и напряжения даже при небольшом превышении критического значения.
33
§ 5.2. Формула Эйлера определения критической силы
Леонард Эйлер (Leonard Euler, 1707 – 1783) – величайший математик, физик, механик, астроном. Родился в Швейцарии, но более 30 лет жил в Петербурге; академик Петербургской Академии Наук.
Предварительно заметим, что существуют различные методы исследования устойчивости, которые рассматриваются в специальных курсах: например, известен курс «Устойчивость сооружений». Метод Эйлера является наиболее простым для решения задач инженерной практики. Метод основан на анализе разветвления возможных форм равновесия упругой системы. Повторим рассуждения Эйлера. Формула была выведена для случая шарнирного закрепления концов стержня (рис. 5.2), причем Эйлер доказал, что деформированная ось стержня (на рисунке показана тонкой линией) – полуволна синусоиды. В дальнейшем изогнутую ось стержня в случае потери устойчивости так и называют – полуволна синусоиды Эйлера.
| Рис. 5.2 |
| F |
 |
Известно приближенное дифференциальное уравнение упругой линии
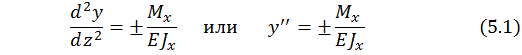
34
Справа в выражении (5.1) использовано распространенное обозначение производной штрихами; два штриха обозначают вторую производную: 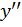 =
= 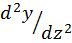 .
.
Мы будем рассматривать принятую нами ранее систему координат (на рис. 5.2 она не показана): начало координат поместим в нижней опоре; вдоль стержня направим ось z вверх; перпендикулярно ей ось y влево от начала координат. Выбранной системе координат соответствует знак плюс в уравнениях (5.1):
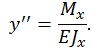
| (5.2) |
В правой части записанных выражений (5.1) и (5.2) 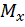 – изгибающий момент в произвольном сечении балки на расстоянии
– изгибающий момент в произвольном сечении балки на расстоянии 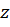 от начала координат;
от начала координат; 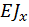 – жесткость сечения балки при изгибе.
– жесткость сечения балки при изгибе.
Замечание. Дифференциальное уравнение упругой линии можно использовать и при изучении устойчивости сжатых стержней, так как потеря устойчивости стержня возникает при малых деформациях, т. е. справедлива гипотеза о малости деформаций.
В произвольном сечении стержня (отсчет от начала координат) с абсциссой z изгибающий момент имеет значение
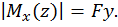
Тогда (5.2) перепишем с учетом выражения момента, дополнительно учтем правило знака между прогибом и второй производной прогиба:
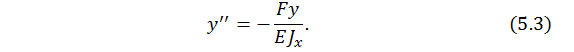
Обратим внимание: появился знак минус! Существует правило: прогиб (y) и вторая производная прогиба ( 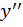 ) всегда разнозначны независимо от выбора положительного направления оси ординат.
) всегда разнозначны независимо от выбора положительного направления оси ординат.
35
Введем дополнительно обозначение:
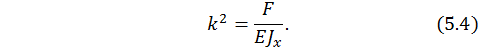
Тогда выражение (5.3) примет вид
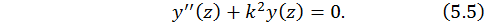
Получили однородное дифференциальное уравнение второго порядка. Общий интеграл этого уравнения (известно из высшей математики) представляет собой выражение вида
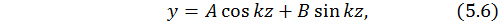
где 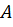 и
и 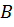 – некоторые коэффициенты, которые можно найти из граничных условий по концам стержня.
– некоторые коэффициенты, которые можно найти из граничных условий по концам стержня.
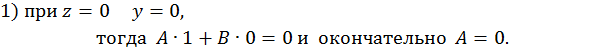
С учетом найденного значения для 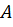 выражение (5.6) принимает более простой вид:
выражение (5.6) принимает более простой вид:
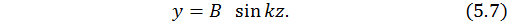
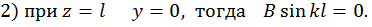 Таким образом, получаем
Таким образом, получаем
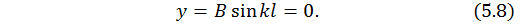
Уравнение (5.8) верно, если один из сомножителей равен нулю.
Если 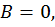 то в выражении (5.6) заведомо
то в выражении (5.6) заведомо 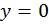 , а это не соответствует условию задачи.
, а это не соответствует условию задачи.
Очевидно, второй сомножитель должен быть равен нулю, т. е. 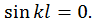
36
Решением этого тригонометрического уравнения является
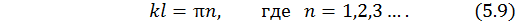
Возводим в квадрат обе части выражения (5.9), получим
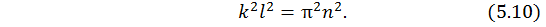
Отсюда выразим 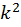
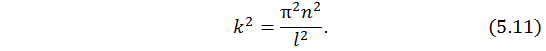
Вспомним о введенном ранее обозначении (5.4) и приравняем правые части (5.4) и (5.11), получим:
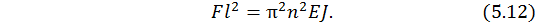
Выразим значение силы в виде
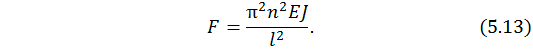
Таким образом, получили выражение критической силы в виде (5.13). Как видим из формулы, существует не одна, а множество значений критической силы в силу изменения параметра n. Очевидно, наименьшее значение критической силы имеем при минимальном значении n , т.е. при 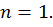
Для прямых стержней известна формула Эйлера в виде
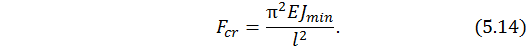
Здесь 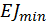 – минимальная жесткость сечения стержня при изгибе;
– минимальная жесткость сечения стержня при изгибе; 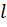 – длина сжатого стержня.
– длина сжатого стержня.
37
Важно. Потеря устойчивости происходит в плоскости наименьшей жесткости!
Выводы. 1. Если 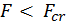 , то возможна только прямолинейная форма равновесия, которая в этом случае является устойчивой.
, то возможна только прямолинейная форма равновесия, которая в этом случае является устойчивой.
2. Для стержня, работающего в упругой стадии, критическая сила зависит только от геометрических размеров стержня и модуля упругости, но совершенно не зависит от прочностных характеристик материала стержня.
Далее на рис. 5.3 показаны возможные формы потери устойчивости при 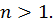 (на рисунке изображены красными линиями)
(на рисунке изображены красными линиями)

Рис. 5.3
Практический расчет
центрально-сжатых стержней на устойчивость
В реальных условиях работы необходимо, чтобы сжатый стержень находился в устойчивом равновесии и имел определенный запас устойчивости. Это состояние обеспечивается в том случае, если действующая нагрузка меньше критического значения. Для обеспечения запаса устойчивости вводится коэффициент, уменьшающий расчетное
44
сопротивление на сжатие до значения, которое гарантирует устойчивость прямолинейной формы равновесия. Условие сохранения устойчивости имеет вид
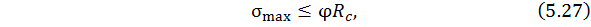
где 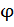 – коэффициент продольного изгиба (или коэффициент уменьшения основного расчетного сопротивления при продольном изгибе);
– коэффициент продольного изгиба (или коэффициент уменьшения основного расчетного сопротивления при продольном изгибе); 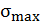 – максимальное расчетное нормальное напряжение. Коэффициент
– максимальное расчетное нормальное напряжение. Коэффициент 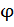 является функцией гибкости стержня, то есть
является функцией гибкости стержня, то есть 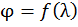 . Следовательно, он зависит от размеров и формы поперечного сечения стержня. Значения коэффициента продольного изгиба для различных
. Следовательно, он зависит от размеров и формы поперечного сечения стержня. Значения коэффициента продольного изгиба для различных
гибкостей разных материалов установлены СНиПами и обычно приводятся в виде таблиц (см., например, далее табл.5.1) или эмпирических формул. Например, для деревянных элементов
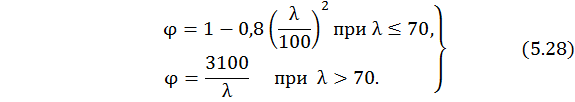
Обратимся вновь к условию (5.27). Как правило, его можно использовать для проверки устойчивости стержня, для выполнения проектировочного расчета и для определения допускаемой нагрузки.
Проверка устойчивости. Нормальные напряжения при центральном
сжатии определяются как 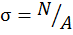 , тогда условие устойчивости с учетом равенства
, тогда условие устойчивости с учетом равенства 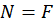 принимает вид
принимает вид
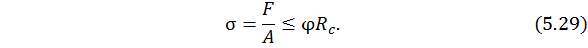
45
Проверка устойчивости выполняется непосредственно по формуле (5.29): все параметры заданы, значение коэффициента продольного изгиба 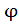 легко находится по таблице зависимости от гибкости стержня λ (вспомним, что гибкость находят на основе заданных геометрических параметров стержня).
легко находится по таблице зависимости от гибкости стержня λ (вспомним, что гибкость находят на основе заданных геометрических параметров стержня).
Проектировочный расчет обычно проводится как задача подбора поперечного сечения стержня. В этом случае условие (5.29) рассматривается в виде
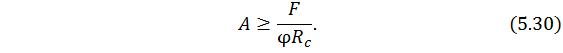
В записанном соотношении площадь поперечного сечения 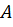 является неизвестной величиной; коэффициент продольного изгиба
является неизвестной величиной; коэффициент продольного изгиба 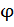 также неизвестен, так как параметры поперечного сечения не заданы и вычислить значение гибкости невозможно. Для решения задачи в этой
также неизвестен, так как параметры поперечного сечения не заданы и вычислить значение гибкости невозможно. Для решения задачи в этой
постановке используется метод последовательных приближений.
Глава 6
БАЛОК И РАМ МЕТОДОМ СИЛ
Стержневой системы
Статически неопределимой стержневой системой называют систему, которая не может быть рассчитана с использованием только уравнений равновесия – уравнений статики. В такой системе существуют лишние с точки зрения уравнений статики связи. В дальнейшем будем рассматривать стержневые статически неопределимые системы.
Условно можно выделить два вида статической неопределимости:
1) внешняя неопределимость – наблюдается в статически неопределимых системах, в которых существуют лишние опорные закрепления. В этом случае из уравнений статики нельзя найти все опорные реакции.
2) внутренняя неопределимость – наблюдается в системах с лишними связями, введенными для взаимного соединения частей системы. В этом случае из уравнений равновесия нельзя найти все внутренние силовые факторы.
Существуют различные методы расчета статически неопределимых систем. Важнейшими из них являются: метод сил, метод перемещений, смешанный метод и др. (Эти методы подробно рассматриваются в дисциплине «Строительная механика».) Здесь же рассмотрим более подробно расчет статически неопределимых систем методом сил на действие неподвижной нагрузки. Название метода подсказывает, что за неизвестные при использовании этого метода приняты силы – фактические усилия в лишних связях. Именно для неизвестных сил будут рассматриваться определенные уравнения. Но расчет начинается с определения степени статической неопределимости.
49
Основной характеристикой статически неопределимых систем является степень статической неопределимости – количество «лишних» связей, которые необходимо мысленно удалить из статически неопределимой системы для преобразования ее в статически определимую. Заметим, что слово «лишние» заключено в кавычки не случайно: некоторые связи являются лишними с точки зрения уравнений статики (их количество является недостаточным). На практике статически неопределимые системы являются более жесткими системами по сравнению с системами статически определимыми.
Степень статической неопределимости n для плоских систем находится по различным формулам. Наиболее простой является следующая формула:
1) 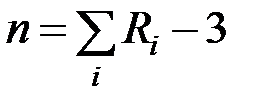 .
.
Здесь 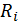 - количество опорных реакций в системе, суммирование проводится по количеству реакций. Число «3» указывает, что для плоского случая существуют три уравнения равновесия – три уравнений статики. Но эта формула неприменима для систем, имеющих замкнутые контуры. Для них применяется формула в виде:
- количество опорных реакций в системе, суммирование проводится по количеству реакций. Число «3» указывает, что для плоского случая существуют три уравнения равновесия – три уравнений статики. Но эта формула неприменима для систем, имеющих замкнутые контуры. Для них применяется формула в виде:
2) 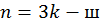 ,
,
где 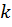 – число замкнутых контуров, включая опорные, которые можно образовать в системе; ш – общая кратность всех шарниров. Кратность шарнира – величина, на единицу меньшая количества соединяемых шарниром стержней. На рис. 6.1 показаны примеры вычисления кратности. Значение кратности показано цифрой рядом с шарниром.
– число замкнутых контуров, включая опорные, которые можно образовать в системе; ш – общая кратность всех шарниров. Кратность шарнира – величина, на единицу меньшая количества соединяемых шарниром стержней. На рис. 6.1 показаны примеры вычисления кратности. Значение кратности показано цифрой рядом с шарниром.
| 1 |
| 2 |
| 3 |
Рис. 6.1
Вычисление степени статической неопределимости проиллюстрируем примерами, показанными на рис. 6.2. Обратим внимание на
50
вычисление степени статической неопределимости на рис. 6.2, б: из общего количества реакций (в каждой жесткой заделке существует по три реакции) вычитается число 4 (а не 3, как в формуле). В этом случае к количеству уравнений равновесия на плоскости добавляется уравнение равновесия в виде суммы изгибающих моментов относительно шарнира самой системы. Кратность шарнира в примере равна единице, поэтому добавлено одно уравнение. В примерах рис. 6.2, в и г степень статической неопределимости вычисляется через замкнутые контуры (римскими цифрами пронумерованы замкнутые контуры, уже существующие или образованные).
а) б)
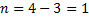
|
| 1 |
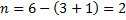
|
| 2 |
| 1 |
| 1 |
| 2 |
| I |
| IIII |
| IIIII |
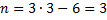
|
| 1 |
| 1 |
| I |
| II |
| 1 |
| 1 |
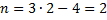
|
Рис. 6.2
51
Столетовых»
(ВлГУ)
С. А. МАВРИНА
НЕКОТОРЫЕ ВОПРОСЫ ТЕОРИИ СОПРОТИВЛЕНИЯ МАТЕРИАЛОВ
ЛЕКЦИОННЫЙ КУРС ДЛЯ ВЫПОЛНЕНИЯ РАСЧЕТНО-ГРАФИЧЕСКИХ РАБОТ
2018
УДК 539.3
ББК 30.121
Рецензент
Кандидат технических наук,
доцент кафедры «Строительное производство»
С. В. Прохоров
Некоторые вопросы теории сопротивления материалов. Лекционный курс для выполнения расчетно-графических работ: Учебное электронное издание / Владим. гос. ун-т; сост. С. А. Маврина. – Владимир, 2018. – 62 с.
Содержатся теоретические основы сложного сопротивления, устойчивости и расчета статически неопределимых систем методом сил в сопротивлении материалов.
Предназначены для студентов, обучающихся по направлению «Строительство». Ориентировано для студентов очной, заочной и заочной с элементами дистанционных технологий форм обучения.
Табл. 1. Ил. 22. Библиогр.: 6 назв.
УДК 539.3
ББК 30.121
Глава 1. ОСНОВНЫЕ ПОНЯТИЯ
Введение
«Сопротивление материалов» – раздел механики твердого деформируемого тела, в котором изучается поведение различных тел под нагрузкой. В общепринятом смысле сопротивление материалов рассматривается как наука об инженерных методах расчета на прочность, жесткость и устойчивость отдельных элементов конструкций и простых систем. В курсе сопротивления материалов решаются три основные задачи:
● изложение методов расчета элементов конструкций на прочность.
● изложение методов расчета элементов конструкций на жесткость.
●изложение методов расчета элементов конструкций на устойчивость.
Решение указанных задач в сопротивлении материалов основано на использовании ряда гипотез и допущений, схематизации реальных тел и нагрузок.
Дата: 2019-02-25, просмотров: 373.