Термин «развивающее обучение» методисты используют с большой осторожностью. Сложные динамические связи между процессами обучения и психического развития ребёнка не являются предметом исследования методической науки, в которой реальные практические результаты обучения принято описывать на языке знаний, умений и навыков. Так как изучением психического развития ребёнка занимается психология, то при построении развивающего обучения методика, несомненно, должна опираться на результаты исследований этой науки. В.В.Давыдов: «Психическое развитие человека – это, прежде всего, становление его деятельности, создания и, конечно, всех «обслуж ивающих» их психических процессов.» Следовательно, развитие учащихся во многом зависит от той деятельности, которую они выполняют в процессе обучения. Деятельность может быть продуктивной и репродуктивной.
Репродуктивная деятельность характеризуется тем, что ученик получает готовую информацию, воспринимает её, понимает, запоминает, затем воспроизводит. Основная цель такой деятельности – формирование у школьника знаний, умений и навыков, развитие внимания и памяти.
Продуктивная деятельность связана с активной работой мышления и находит своё выражение в таких мыслительных операциях, как анализ и синтез, сравнение, классификация, аналогия, обобщение. Эти мыслительные операции принято называть логическими приёмами мышления или приёмами умственных действий. Продуктивные методы обучения ориентированы на стимулирование познавательной деятельности детей при овладении новыми знаниями (деловые игры, исследовательский эксперимент, эвристическая беседа, методы проблемного обучения, самостоятельная (творческая) работа в микрогруппах и парах).
Продуктивные методы не противопоставляются репродуктивным. Важно дидактически целесообразное сочетание этих методов на различных этапах в зависимости от целей и содержания обучения.
Организация развивающего обучения предполагает со здание условий для овладения школьниками приёмами умственной деятельности. Овладение ими не только обеспечивает новый уровень усвоения, но даёт существенные сдвиги в умственном развитии ребёнка. Овладев этими приёмами, ученики становятся более самостоятельными в решении учебных задач, могут рационально строить свою деятельность по усвоению знаний.
Рассмотрим возможности активного включения в процесс обучения математике различных приёмов умственных действий.
Сравнение – логический метод, используемый в математике. В результате сравнения выделяются сходство и различие сравниваемых предметов, т.е. наличие у них общих и не общих свойств.
Для организации деятельности учащихся, направленной на выделение признаков того или иного
объекта, можно сначала предлагать вопросы в форме:
- Что вы можете рассказать о предмете? (Яблоко круглое, большое, красное. Тыква – жёлтая, большая, с полосками, с хвостиком…)
В процессе работы учитель знакомит детей с понятиями «размер», «форма» и предлагает следующие вопросы:
- Что вы можете сказать о размерах (формах) этих предметов? (Большой, маленький, круглый, треугольный…)
Для выявления признаков или свойств нескольких предметов обращаются с вопросами:
- 
 В чём сходство и различие этих предметов? Что изменилось?
В чём сходство и различие этих предметов? Что изменилось?
- форма
- 
 размер и т.д.
размер и т.д.
Умение выделять признаки и, ориентируясь на них, сравнивать предметы, формируется следующими упражнениями:
1. В чём сходство и различие: а) выражений 6+(7+3) и (6+7)+3; 3∙2 и 2∙3; 5+1 и 5-1;
б) чисел 3 и 33; 216 и 16; 48 и 84 и др.
в) равенств 7∙(1+8)=63 и 7∙1+7∙8=63; 3∙(7∙10)=210 и (3∙7)∙10=210.
г) текстов задач: «Коля поймал 2 рыбки, Петя – 6. На сколько больше поймал рыбок Петя, чем Коля?» и «Коля поймал 2 рыбки, Петя – 6. Во сколько раз больше поймал рыбок Петя, чем Коля?»
д) геометрических фигур
е) уравнений 3+х=5, х+3=5;
ж) вычислительных приёмов 9+6=(9+1)+5 и 6+3=(6+2)+1
В обучении младших школьников большая роль отводится упражнениям, которые связаны с переводом предметных действий на язык математики. Например: а) какому рисунку соответствуют записи 4∙2 и 4+2

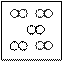 | 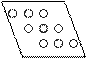 |  | |||
б) какой рисунок соответствует записи 4∙3? Если такого рисунка нет, то нарисуй его.
в) выполни рисунки, соответствующие записям 8+2; 8-6; 3∙3.
Показатель сформированности приёма сравнения – умение детей самостоятельно использовать его для решения различных задач, без указания: «сравни …», «укажи признаки…», «в чём сходство и различие».
А) Убери лишний предмет.
Б) Расположи числа в порядке возрастания (убывания)
В) Сумма чисел в первом столбике 76. Как, не выполняя сложения во втором и третьем столбиках, найти сумму чисел?
Г) Продолжи ряд чисел 0, 3, 6, 9, 12, 15, …
Правильный вывод можно получить, если выполняются следующие условия: а) сравниваемые понятия однородны, б) сравнение осуществляется по существенным признакам.
Классификация Основа приёма классификации – умение выделять признаки предметов и
устанавливать между ними сходство и различие. Следует помнить, что при разбиении множества на классы необходимо выполнять следующие условия: 1) ни одно из подмножеств не пусто; 2) подмножества попарно не пересекаются; 3) объединение всех подмножеств составляет данное множество.
При обучении математике можно использовать следующие виды заданий на классификацию:
1) Подготовительные задания: «Убери (назови) лишний предмет», «Нарисуй предметы такого же цвета (формы, размера)», «Дай название группе предметов» и др.
2) Задания, в которых на основание классификации указывает учитель.
3) Задания, при выполнении которых дети сами выделяют основание классификации.



 У школьников умение выполнять классификацию формируется в тесной связи с изучением конкретного содержания. Например, для упражнений в счёте им часто предлагаются иллюстрации, к которым можно поставить вопрос со слова «Сколько
У школьников умение выполнять классификацию формируется в тесной связи с изучением конкретного содержания. Например, для упражнений в счёте им часто предлагаются иллюстрации, к которым можно поставить вопрос со слова «Сколько


 …»
…»
Сколько больших кругов? Маленьких? Синих? Больших красных?
Маленьких синих? и т.д.
По мере изучения различных понятий задания на классификацию могут включать числа, выражения, равенства, уравнения, геометрические фигуры. Например:
1. Разбейте данные числа на две группы, чтобы в каждой оказались похожие числа:
а) 33, 84, 75, 22, 13, 11, 44, 53; б) 91, 81, 82, 95, 99, 80, 85; в) 45, 36, 25, 54, 52, 61, 63, 54, 43, 27, 34, 72.
2. Разбейте данные выражения на группы 3+1, 4-1, 5+1, 6-1, 7+1. В заданиях учитель может специально оговаривать, на сколько групп нужно разбить множество.
3. При знакомстве с четырёхугольником можно предложить задание:
- Убери лишнюю фигуру. Чем похожи все остальные фигуры? Как можно назвать эти фигуры? Покажи четырёхугольник с одним прямым углом, с двумя, с тремя и четырьмя прямыми углами. Разбей четырёхугольники на группы по количеству прямых углов.
Анализ и синтез. Анализ связан с выделением элементов данного объекта, его признаков или свойств. Синтез – это соединение различных элементов, сторон объекта в единое целое. В мыслительной деятельности человека анализ и синтез дополняют друг друга. Способность к аналитико -синтетической деятельности находит своё выражение не только в умении выделять элементы того или иного объекта, его различные признаки или соединять элементы в единое целое, но и в умении включать их в новы е связи, увидеть их новые функции.
Формированию этих умений может способствовать:
а) рассмотрение данного объекта с точки зрения различных понятий; б) постановка различных заданий к данному математическому объекту.
Например:
1. Прочитай по-разному выражение 10-8 (10 уменьшили на 8, разность чисел 10 и 8).
2. Прочитай по-разному равенство 26-6=20 (26 уменьшить на 6, получим 20; 26 больше 20 на 6; разность чисел 26 и 6 равна 20; 26 – уменьшаемое, 6 – вычитаемое, 20 – разность и др.)
3. Как по-разному можно назвать квадрат?
4. Расскажи всё, что ты знаешь о числе 319.
5. По каким признакам можно разложить пуговицы в две коробки? (по форме и числу дырочек)
6. Разгадай правило, по которому составлена таблица и заполни пропущенные клетки
| 3 | 7 | 9 | 4 | 5 | 6 | 1 | 8 | ||
| 4 | 8 | 8 | 3 | 2 | 6 |
7. Найди отрезок АВ. Что ты можешь рассказать о нём?
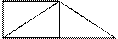
А
В
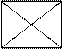
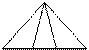
8. Сколько треугольников на данном чертеже? Сколько многоугольников? Сколько отрезков?
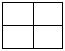 | |||||
 |  | ||||
Приём обобщения – выделение существенных признаков математических объектов. Следует различать результат и процесс обобщения. Результат фиксируется в понятиях, суждениях, правилах. Процесс же обобщения может быть организован либо на эмпирическом, либо на теоретическом уро вне. Эмпирические методы – наблюдение, опыт, измерения.
Традиционно в начальном курсе математики наиболее часто применяется эмпирический тип, при
котором обобщение знания является результатом индуктивных рассуждений. Восхождение от частного к общему, от фактов, установленных с помощью наблюдения и опыта, к общим закономерностям имеет логическую форму рассуждения «от частного к общему» и называется индукцией. Используя индуктивные умозаключения, учащиеся могут самостоятельно «открывать» математические свойс тва и способы действий (правила, законы), которые в математике строго доказываются.
Для получения правильного обобщения индуктивным способом необходимо:
1) продумать подбор математических объектов и последовательность вопросов для целенаправленного наблюдения и сравнения;
2) рассмотреть как можно больше частных объектов, в которых повторяется та закономерность, которую ученики должны подметить;
3) варьировать виды частных объектов, т.е. использовать предметные ситуации, схемы, таблицы, выражения, отражая в каждом виде объекта одну и ту же закономерность;
4) помогать детям словесно формулировать свои наблюдения, задавая наводящие вопросы, уточняя и корректируя те формулировки, которые они предлагают.
Например: 1. 2+5=5+2
7+3=3+7 Отсюда следует а+в=в+а
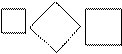
2. Рассмотрите прямоугольники, представленные на рисунке. Чем они похожи? Все стороны этих прямоугольников равны. Отсюда следует: квадрат – прямоугольник с равными сторонами.

Индукция не всегда может служить методом доказательства в математике (невозможно исчерпать все частные случаи). Формируя у младших школьников умение обобщать наблюдаемые факты индуктивным путём, полезно предлагать задания, при выполнении которых они могут сделать неверные обобщения.
Например:
1. Проверь, будет ли делиться каждое слагаемое на 2 и сделай вывод: (2+4):2=3, (4+4):2=4, (6+2):2=4, (6+8):2=7. Дети могут придти к заключению: «если сумма чисел делится на 2, то каждое слага емое этой суммы делится на 2».
2. Сравни выражения, найди общее в полученных неравенствах и сделай вывод:
2+3…2∙3, 4+5…4∙5, 5+6…5∙6. Вывод: сумма двух последовательных чисел всегда меньше их произведения.
Большинство педагогов и психологов считают, что эмпирическое обобщение для младших школьников
наиболее доступно. Поэтому обучаясь по традиционной методике, сравнивая математические объекты или способы действий, ребёнок выделяет их внешние общие свойства, которые могут стать содержанием понятия. А этот ориентир на внешние, доступные для восприятия свойства сравниваемых математических объектов не всегда позволяет раскрыть сущность изучаемого понятия или усвоить общий способ действий. Это отрицательно сказывается на формировании понятий и общих способов действий. Например, большинство детей усваивают понятие «больше на» только в результате однообразных тренировочных упражнений, которые выражаются в способе действий с конечными множествами: взять столько же и ещ ё (это отношение на величинах традиционно не вводится). Поэтому дети способны выполнить те или иные рассуждения только в рамках данной конкретной ситуации и на ограниченной области чисел.
Теоретическое обобщение осуществляется путём анализа данных о каком -либо одном объекте или ситуации с целью выявления существенных внутренних связей. Эти связи сразу фиксируются абстрактно (теоретически- с помощью слова, знаков, схем) и становятся той основой, на которой в дальнейшем выполняются частные (конкретные) действия. Необходимое условие формирования у младших школьников способности к теоретическому обобщению – направленность обучения на формирование общих способов деятельности. Для выполнения этого условия нужно продумать такие действия с математическими объектами, в результате которых дети смогут сами «открывать» существенные свойства изучаемых понятий и общих способов действий с ними.
В настоящее время это одна из самых актуальных проблем начального обучения, решение которой связано как с изменением содержания, так и с изменением организации учебной деятельности младших школьников, направленной на его усвоение.
Дедуктивное рассуждение – рассуждение от общего к частному. В дедуктивном рассуждении нельзя получить ложное заключение из истинных посылок. Именно поэтом у дедуктивные рассуждения используются в математических доказательствах. Возможно ли обучение доказательству младших школьников? По мнению психологов А.В.Запорожца, К.Н.Некрасовой, В.В.Давыдова, М.В.Крыловой, Эрдниева и др. работа по формированию умения до казывать математические предложения может начинаться уже в 1 классе. Подготовка младших школьников к осознанному усвоению и проведению строгих математических доказательств предполагает: 1) воспитание у детей потребности в аргументации высказываемых суждений и осознание ими необходимости доказательств; 2) использование в обучении доступных для данного возраста способов обоснования истинности математических предложений и постепенное овладение учениками наиболее употребительными из них.
Пример: умножение натуральных чисел коммутативно.
Для доказательства возьмём прямоугольник, разбитый на квадраты: 1) если считать квадраты по горизонтали, получим АхВ; 2) если вести их счёт по вертикали, получим ВхА; 3) число в данном прямоугольнике не зависит от способа счёта; 4) следовательно АхВ=ВхА.
Требования к уроку математики школы 5 вида
1. Каждый урок должен иметь четко сформулированную тему и цель. Так как урок математики включает и арифметический и геометрический материал, то на уроке может быть поставлена не одна, а несколько дидактических целей. Неоднозначность цели на уроке обусловлена необходимостью включать почти в каждый урок новый материал, повторять пройденное и готовить учащихся к восприятию новых знаний. Однако на каждом уроке математики должна быть о дна главная дидактическая цель. Наряду с учебными целями формируются коррекционно-развивающие и воспитательные цели.
2. Содержание учебного материала на уроке должно отвечать теме, целям урока, быть доступно учащимся, отвечать требованиям индивидуального и дифференцированного подхода, научно, тесно связано с жизнью и трудом.
На уроке необходимо сочетание арифметического и геометри ческого материала, теоретического и практического материала, упражнений вычислительного характера и решения задач.
Объем учебного материала должен обеспечить активность учащихся и работу в течение урока в доступном темпе.
3. Методы и приемы работы на уроке должны отвечать возрастным особенностям школьников, развивать и коррегировать их познавательную деятельность, способствовать формированию умственных и практических действий, способностей анализировать, синтезировать, обобщать.
4. На каждом этапе урока математики ведется систематический контроль за качеством усвоения знаний, формированием умений и навыков.
Учитель ставит перед учащимися конкретные цели и добивается от каждого ученика (в зависимости от его
возможностей) их реализации, осуществляет контроль за деятельностью школьников, вносит коррективы в их знания, оказывает необходимую помощь, укрепляет уверенность, поощря ет даже минимальные успехи.
5. Урок должен быть оснащен необходимыми наглядными посо биями и дидактическим материалом,
учебниками и тетрадями (в клетку и без линеек для работ по геометрии), измерительными и чертежными инструментами, техническими средствами. Следует отметить, что для детей-логопатов со сниженным интеллектом одновременно должно демонстрироваться не более 1—2 наглядных пособий.
6. Каждый урок математики должен отличаться организационной четкостью: ясная цель каждой структурной части урока и подчиненность их главной дидактической цели урока, четкое пла нирование урока и правильное распределение времени между каждой структурной частью. Сочетание фронтальной работы с индивидуальным и дифференцированным подходом.
7. Повторение должно осуществляться на каждом уроке математики, т. е. должен соблюдаться принцип непрерывности повторения.
8. На каждом уроке учитель должен развивать речь учащихся, обогащать их словарь новыми терминами и
выражениями, следить за точностью, лаконичностью и грамма тическим строем речи.
9. Уроки математики должны быть тесно связаны с другими учебными предметами.
10. Уроки математики должны носить практическую направленность, способствовать решению задач социальной адаптации и реабилитации учащихся с ТНР коррекционной школы.
11. Учитель должен служить образцом подражания для учащихся: прекрасное знание учебного материала, владение методикой его проведения, собранность, четкость инструкций, лаконичная речь, эмоциональность, доброжелательное отношение к учащимся.
12. Урок математики должен будить не только мысль, но и чувства. Учитель должен не забывать об эмоциональной стороне урока и воспитывать любознательность и интерес к математичес ким фактам и явлениям.
13. На уроках математики должны быть реализованы требования лечебно-педагогического режима с учетом работоспособности и утомляемости учащихся с ТНР. Этому способствует переключение видов деятельности, проведение физкультминуток, целесообразное распределение учебного материала и видов работ и т.д.
Вопросы и задания для самоконтроля.
1. Дидактические игры на уроках математики, их роль в коррекционно -развивающем обучении. Разработайте фрагменты конспектов занятий и уроков с использованием дидактических игр.
2. Обоснуйте методы и средства обучения математике (на примере начальной школы).
3. Раскройте основные формы организации учебной деятельности в начальной школе при обучении математике. Типы уроков, их классификация.
4. Раскройте специфику коррекционного урока по математике.
5. Раскройте методику развития приёмов умственных действий на математике начального курса математики. Приведите примеры заданий, направленных на развитие приёмов умственных действий.
6. Подготовьте сообщения на темы: «Индивидуальные особенности и способности школьников с
речевой патологией в контексте изучения курса математики»; «Математические способности и обучаемость»; «Суть личностно-ориентированного обучения».
Глава 5. Вопросы формирования математических представлений у детей дошкольного возраста с речевыми нарушениями
Дата: 2019-02-25, просмотров: 783.