Методика преподавания математики (или дидактика математики, педагогика математики) – наука, предметом которой является обучение математике, причём в широком смысле: обучение математике на всех уровнях, начиная с дошкольных учреждений и кончая высшей школой . Методика преподавания математики (МПМ) в образовательных учреждениях для детей с нарушениями речи может быть определена как научная область, направленная на поиск технологий обучения математике детей, имеющих специфические проблемы речевого развития.

Различают три уровня обучения (или три теории): психологический, общепедагогический и методический. Общепедагогическая теория обучения (дидактика) строится на базе определённой психологической концепции (теории) обучения. Однако дидактика не учитывает характерные особенности учебного предмета. Разработка теории обучения с учётом специфики учебного предмета и есть методический уровень теории обучения, или методическая теория обучения, в нашем случае – методика преподавания математики в школе для детей с нарушениями речи.

МПМ развивается на базе определенной психологической концепции обучения и общедидактической теории. Кроме того, МПМ должна учитывать особенности физиологического и психологического развития детей с тяжёлыми речевыми нарушениями. А также в ней должна отражаться специфика предмета обучения

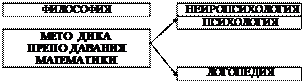
1.2.

Обучение – сложный процесс управления познавательной деятельностью учащихся, осуществляемый учителем с использованием вспомогательных средств (учебников, наглядных пособий, технических средств обучения и т.д.). Обучение включает восприятие, переработку, хр анение и обмен информацией между двумя участниками процесса (учителем и учеником). Процесс обучения должен предполагать учёт структуры нарушения речи и индивидуально-типических особенностей лиц с речевой патологией. Поэтому предметом МПМ в школе для детей с нарушениями речи является коррекционно -развивающее обучение детей- логопатов. Коррекция предполагает систему педагогических, психологических и медицинских мер, направленных на устранение отклонений в речевом, психическом и общеличностном развитии. В проц ессе коррекции происходит изменение негативных установок и мотивации на позитивные, пассивной позиции в речевой деятельности на активную, снятие тревожности, неуверенности, закомплексованности. В ходе коррекции происходит компенсация временно утраченных р езервов личности, функций речи, т.е. восстановление, перестройка или их замещение. Их несформированность тормозит общеличностное развитие. Развитие – это внутренний процесс самодвижения и самореализации личности, котор ый происходит под влиянием внутренних и внешних условий. В ходе развития появляются новообразования в личности обучаемых, т.е. новые качественные изменения в потребностно -мотивационной, эмоционально- волевой, интеллектуальной, поведенческой сферах.

Задачи коррекционной методики обучения математике детей с нарушением речи:

· определить образовательные, воспитательные и коррекционно -развивающие возможности процесса обучения математике в образовательных учреждениях 5 вида;

· охарактеризовать специфические трудности усвоения математических понятий, знаний и умений характерные для детей с различной структурой нарушения речевой деятельности;

· определить  содержание обучения математике детей дошкольного и младшего школьного возраста с тяжёлыми нарушениями речи (ТНР);

· обосновать принципы, методические по дходы и формы организации деятельности обучаемых с

ТНР;

· разрабатывать и совершенствовать методику коррекционно -развивающей, учебно-воспитательной

и консультативной видов деятельности педагога-логопеда.

Образовательные , воспитательные, коррекционно-развивающие задачи в структуре учебной деятельности учащихся с речевой патологией

Образовательная задача базируется на понимании того, что дети с нарушением речи должны овладеть тем же объёмом представлений, знаний, умений и навыков, что и дети с нормальным речевым развитием. Он всегда определён в программе с учётом преемственности в обучении. Так образовательные задачи обучения математике дошкольников и младших школьников могут быть сформулированы следующим образом:

· овладение определённой системой математических представлений и понятий и общих способов действий по ведущим содержательным линиям: в дошкольном возрасте «Количественные представления. Представления о числе и множестве», «Представления о форме», «Преставления о величине и измерении величин», «Представления о времени», «Пространственные представления»; в младшем школьном возрасте

«Число и вычисления», «Пространственные отношения. Геометрические фигуры. Измерение геометрических величин»;

· овладение первоначальными представлениями о ведущем математическом методе познания реальной действительности – математическом моделировании;

· формирование общего умения решать задачи.

Содержательная линия «Число и вычисления» даёт учащимся возможность получить представления о натуральном числе как результате счёта и измерения величин, понять особенности построения натурального ряда чисел, освоить принцип позиционной системы записи чисел, овладеть арифметическими действиями с натуральными числами и величинами.

Реализация в обучении второй линии «Пространственные отношения. Геометрические фигуры. Измерение геометрических величин» предоставляет школьникам возможность осознать геометрические формы как образы предметов окружающего мира; познакомиться с различными геометрическими фигурами, открыть некоторые их свойства через преобразование, конструирование, изображение, выполнение простейших дедуктивных умозаключений и измерений.

В процессе освоения данного содержания дети не только получают первоначальные представления о математическом моделировании, о структуре задачи и этапах её решения, но происходит и развитие их логического мышления, мыслительных процессов, умений оперировать знаково -символическими средствами. При формировании математических представлений и понятий важно не только добиваться усвоения знаний, умений и навыков, но и осуществлять мероприятия по коррекции психофизических возможностей детей, прежде всего их речевой деятельности.

В ходе коррекционно-развивающего обучения математике, безусловно, решаются и воспитательные задачи. Они могут быть реализованы в процессе анализа жизненных ситуаций и формирования морально - волевых качеств личности (аккуратности, ответственности, дисциплинированности, организованно сти).

Выполнение практических заданий на установление взаимно -однозначного соответствия, пересчёт и отсчёт предметов, сопоставление предметов по величине и форме, ориентировку в пространстве, измерение требует аккуратности, сосредоточенности, дисциплиниро ванности.

Коррекционно-развивающая задача предполагает преодоление недостатков познавательной деятельности: развитие понимания речи, речевого подражания, расширение пассивного и активного словарного запаса, лексико-грамматических структур, формирование связной речи, развитие сенсорного и интеллектуального потенциала, словесно-логического мышления.

Уроки и занятия по математике позволяют осуществлять коррекцию интеллектуальной и речевой деятельности. В процессе обучения выполнению математических операций дети расширяют пассивный словарный запас, начинают понимать значение обиходно -разговорных слов, а также математических терминов, учатся действовать по инструкции. Требование проговаривать вслед за педагогом ход выполнения задания позволяет активизировать речевое подражание, увеличивать активный словарный запас и развивать регулирующую функцию речи.

Использование разнообразных предметов для составления и сравнения множеств, счёта, определения их величины, формы и положения в пространстве позволяет расширять и вербализировать чувственный опыт. Обобщение наглядно-практических действий и математических операций создаёт предпосылки для развития словесно-логического мышления.

У детей развивается грамматический строй речи. Формирование представлений о множестве позволяет показать изменение имён существительных по числам (дом – дома; сова – совы). Происходит обучение согласованию по родам, числам и падежам существительного с числительным (много уток, две утки, три мяча, семь мячей), с порядковыми числительными (первый снег, второй хлопок), с прилагательным, характеризующим величину предмета (маленькая кукла, у высокого дуба, на узкой дороге) . При формировании умения определять пространственное положение и направление движения составляются грамматические конструкции, выражающие отношения между предметами. Дети учатся понимать значение вопросительных и пространственных наречий и предлогов, правильно употреблять их, устанавливать связи между предметом и его действием (книга лежит на столе). Последовательное обучение ори ентировке на плоскости позволяет проводить работу по развитию связной речи. Описание положения предметов на сюжетной картинке является первой ступенью к составлению рассказа, а затем задачи.

Большое коррегирующее значение имеет формирование временных представлений. Дети усваивают глагольные формы, учатся правильно употреблять их. Рассказывают о действиях, совершаемых в определённый период времени.

На уроках математики проводятся дидактические игры, позволяющие включать детей в беседу, строить между ними диалоги, учить межличностному взаимодействию.

Вопросы и задания для самоконтроля.

1. С какими предметами связана методика преподавания математики и в чём проявляется эта взаимосвязь? Обоснуйте свой ответ.

2. Изучите историю становления и развития методики начального обучения математике, в том числе работы исследователей в рамках специальной методики. Проанализир уйте основные периоды развития методики, вклад в развитие методики обучения математике отечественных (М.Мон тессори, Л.С.Выготского, П.Я.Гальперина, В.В.Давыдова, А.М.Леушиной, З.А.Михайловой и др.) и зарубежных психологов и педагогов.

3. Какие задачи стоят перед методикой преподавания математики как научной области?

4. Раскройте специфику образовательных и воспитательных задач решаемых педагогом в процессе обучения математике детей с ТНР?

5. Какие коррекционно-развивающие задачи стоят перед педагогом – логопедом в процессе развития математических способностей ребёнка?

Глава 2. Клинико-пс ихологическая характе рис тика акалькулии и дискалькулии детского возраста