(На практике)

Согласно изложенному материалу, модель (1.3) считается “хорошей”, если

1) она адекватна;

2) она эффективна

3) все ее коэффициенты значимы.

Степень удовлетворения всем перечисленным требованиям при выбранном плане экспериментов зависит от варианта структуры модели, т.е. от типа модели (линейная, квадратичная или иная), а также от того, какие члены в нее включены. Типичным дефектом является наличие незначимых коэффициентов. Обычно с первой попытки хорошую модель построить не удается и надо перебирать различные ее варианты для поиска лучшей. Наиболее обоснованный и качественный вариант модели можно построить так называемым методом возможных регрессий. Согласно ему перебирают все возможные варианты структуры, приемлемые для данного плана экспериментов. Однако требуемый объем работы при этом весьма значителен. Более экономичен и достаточно надежен метод исключения, хотя иногда он не позволяет найти действительно наилучший вариант модели.

Согласно этому методу строят начальный вариант модели, самый сложный для данного плана, с максимальным числом коэффициентов. Оценивают ее адекватность, эффективность и значимость коэффициентов. Если требования 1) – 3) выполняются, то необходимая модель построена. Иначе возможны следующие случаи.

1. (Самый распространенный). Среди членов модели есть незначимые, модель при этом обычно неэффективна (но может быть и эффективной). Тогда надо попытаться улучшить модель, исключив член (один!) с минимальным значением критерия Стьюдента Т_j, пересчитать остальные коэффициенты и проверить новый вариант модели на адекватность, эффективность и значимость коэффициентов. Если после исключения

а) адекватная модель не перестала быть таковой и

б) возросла величина отношения 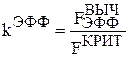, где проверяет эффективность текущего варианта модели и вычисляется по формуле (3.2), а F^КРИТ соответствует критическому значению t_a распределения Фишера и

в) значение увеличилось, или уменьшилось незначительно (не более 10%),

то исключение было сделано правильно, новый вариант модели лучше предыдущего.

Если в новом варианте остались незначимые коэффициенты, то с ним можно повторить исключение, выбрав коэффициент с минимальным значением критерия Стьюдента Т_j, и т. д.

Если же после исключения хотя бы один из пп. а) – в) не выполнился, то исключение выбранного члена не улучшает модель. Если до исключения модель была адекватна и эффективна, то надо остановиться на ее предыдущем варианте. Если при этом в модели остались незначимые коэффициенты, то в принципе, ей можно пользоваться, однако, рекомендуется проверить данные эксперимента. Возможно, в них есть грубые ошибки или просто опытов мало.

Если после очередного исключения в модели остался только свободный член: 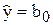, а все предыдущие варианты модели неэффективны, то это означает отсутствие связи между входом и выходом, эффективную модель по имеющимся экспериментальным данным построить невозможно.

2. Модель неадекватна, отбрасывание незначимых членов не улучшает положения. Это означает, что структура модели выбрана неверно. Возможно, следует взять более сложный тип уравнения регрессии (например, вместо линейной – квадратичную).

Пример 4.3. Пусть объект характеризуется двумя входными параметрами х1 и х2. Имеем матрицу плана эксперимента Х и вектор у значений выхода:

; .

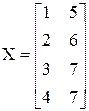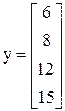Построим по этим данным линейное уравнение регрессии у = b₀ + b₁ x1 + b₂ x2.

Для этого запишем регрессионную матрицу и матрицы, связанные с ней:

; ; .

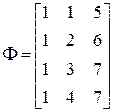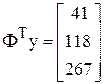В результате применения функции lsolve(Ф^ТФ, Ф^Ту) получаем вектор МНК-оценок, а с его помощью найдем вектор расчетных значений у:

;     .

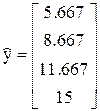Отсюда Q_ОСТАТ = 0.667; Q_ОБЩ = 48.75, следовательно, коэффициент детерминации равен 98.63%, т.е. его значение достаточно велико.

Проверим эффективность модели. F^ВЫЧ = 36.06, при a = 0.05 будет F^КРИТ = 199.5. Следовательно, модель неэффективна.

Оценим значимость коэффициентов. Для этого определим оценку дисперсионной матрицы С:

.

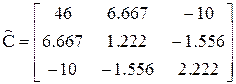Отсюда имеем вектор значений критерия Стьюдента для МНК-оценок

 при Т^КРИТ = 12.706. Следовательно, все коэффициенты незначимы. Таким образом, несмотря на весьма удовлетворительное значение R² модель получилась “нехорошей”.

Исключим из уравнения член с минимальным Т_j., т.е. b₂ x2. Получим модель у =2.5 + 3.1 х1, которая является эффективной: F^ВЫЧ = 137.3, F^КРИТ = 18.5. Новые значения критерия Стьюдента равны (3.45; 11.72) при Т^КРИТ = 4.3. Следовательно, коэффициент при х1 значим, а свободный член “близок к значимому”. Коэффициент детерминации новой модели равен 98.56%, т.е. практически совпадает с показателем первоначального варианта.

Резюме. Итак, для построения наилучшего варианта уравнения регрессии по результатам активного эксперимента надо выполнить следующие действия.

1. Определить область W_х возможных значений входных параметров объекта – область планирования.

2. Определить структуру модели (линейная, квадратичная или иная).

3. Построить план эксперимента, наиболее подходящий для данной модели и области планирования.

4. Провести серию экспериментов в соответствии с выбранным планом.

5. Вычислить значения точечных дисперсий.

6. Проверить гипотезу о постоянстве s² с помощью критерия Кочрена. Если гипотеза неверна, необходимо повторить аномальную серию опытов.

7. Построить модель и провести ее анализ на адекватность, эффективность, значимость коэффициентов.

8. Методом исключения выбрать лучший вариант модели.