Def. Эксперимент называется активным, если исследователь может по своей воле задавать значения входных параметров объекта. В противном случае эксперимент называется пассивным.
Применение активных экспериментов позволяет
- получить более точную модель, не увеличивая число экспериментов;
- оценить адекватность модели.
Характерной чертой активных экспериментов является наличие параллельных опытов.
Def. Параллельные (дублированные) опыты – эксперименты, проводимые при неизменных значениях контролируемых входных параметров.
Очевидно, что при наличии случайных ошибок эксперимента результаты параллельных опытов будут различаться. Пусть каждый опыт, соответствующий i–й экспериментальной точке, повторяется L раз. Обозначим уil (i = 1,…N, l = 1,…, L) – значение параметра у, полученное в i-й точке при l-м параллельном опыте. Согласно МНК, необходимо минимизировать величину
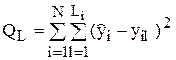 .
.
Как несложно показать
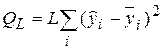 + A,
+ A,
где 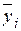 = (å yil) / L – среднее значение выхода в i-й точке. Т.е. Q L отличается от минимизируемой функции Q обычного МНК лишь постоянным множителем и постоянным слагаемым, и вместо непосредственно измеренных значений отклика уi используются их усредненные величины –
= (å yil) / L – среднее значение выхода в i-й точке. Т.е. Q L отличается от минимизируемой функции Q обычного МНК лишь постоянным множителем и постоянным слагаемым, и вместо непосредственно измеренных значений отклика уi используются их усредненные величины – 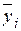 .
.
При наличии L параллельных опытов результаты экспериментов удобно представить в виде (N ´ L)-матрицы Y. Тогда вектор усредненных показателей будет иметь представление 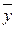 =Ye / L, где e = (1, …, 1)Т– вектор из L единиц. Подставив его вместо вектора у в формулу (1.5) получим
=Ye / L, где e = (1, …, 1)Т– вектор из L единиц. Подставив его вместо вектора у в формулу (1.5) получим
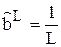 (ФTФ) –1 ФTY e. (3.3)
(ФTФ) –1 ФTY e. (3.3)
Несложно доказать, что оценка (3.3) – несмещенная, а её дисперсия равна
D[ 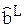 ] =
] = 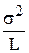 (ФTФ) –1ФTФ(ФTФ) –1 =
(ФTФ) –1ФTФ(ФTФ) –1 = 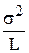 (ФTФ) –1, (3.4)
(ФTФ) –1, (3.4)
т.е. в L раз меньше, чем без параллельных опытов. Соответственно, дисперсия прогноза равна
D[  ] =
] = 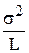 fT(x) (ФTФ) –1f(x). (3.5)
fT(x) (ФTФ) –1f(x). (3.5)
Оценка адекватности модели. Применение параллельных опытов открывает для исследователя новые большие возможности в изучении интересующего его явления. В частности, это касается метода оценки адекватности модели (1.3).
Введем следующие величины, которые назовем точечными дисперсиями
 . (3.6)
. (3.6)
Каждая из них оценивает разброс значений выходного параметра в i–й экспериментальной точке под действием неконтролируемых случайных факторов. Обозначим 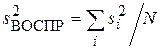 – дисперсия воспроизводимости, которая характеризует средний разброс значений выходного параметра по области значений входных параметров. Имеют место следующие ее свойства.
– дисперсия воспроизводимости, которая характеризует средний разброс значений выходного параметра по области значений входных параметров. Имеют место следующие ее свойства.
Теорема 3.3 (о свойствах дисперсии воспроизводимости).
1) Если дисперсия s2 ошибок эксперимента постоянна во всех экспериментальных точках, то дисперсия воспроизводимости является несмещенной оценкой для s2.
2) Если ошибки эксперимента нормально распределены и независимы, то статистика 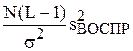 имеет распределение c2 с числом степеней свободы n = N(L – 1).
имеет распределение c2 с числом степеней свободы n = N(L – 1).
Замечание. Наиболее важным моментом теоремы 3.3 является отсутствие требования адекватности модели (1.3), что позволяет использовать 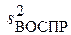 для проверки гипотезы об адекватности уравнения регрессии.
для проверки гипотезы об адекватности уравнения регрессии.
Введем следующую величину 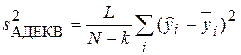 – дисперсия адекватности, представляющую собой аналог остаточной дисперсии, используемый при наличии параллельных опытов.
– дисперсия адекватности, представляющую собой аналог остаточной дисперсии, используемый при наличии параллельных опытов.
Теорема 3.4 (об адекватности уравнения регрессии). Если выполнены условия теоремы 3.3, модель (1.3) имеет свободный член b0 и адекватна, то статистика 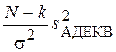 имеет распределение c2(N – k) и независима от
имеет распределение c2(N – k) и независима от 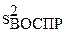 .
.
С помощью этой теоремы мы сможем оценить адекватность модели (1.3). Выдвинем статистическую гипотезу Н0 об адекватности. Если она верна, то статистики  и
и 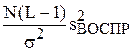 независимы и имеют распределение c2(N – k) и c2(N(L – k)), соответственно. Следовательно, Н0 проверяется с помощью критерия Фишера
независимы и имеют распределение c2(N – k) и c2(N(L – k)), соответственно. Следовательно, Н0 проверяется с помощью критерия Фишера
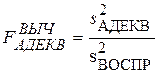 (3.7)
(3.7)
с правосторонней критической областью: если FВЫЧ < t1–a то основная гипотеза верна и модель (1.3) адекватна.
Однородность точечных дисперсий. Напомним, что по теореме Гаусса-Маркова, всё перечисленное выполняется только при условии постоянства значения s2. Соответствующее предположение также можно сформулировать в виде статистической гипотезы, которая проверяется с помощью критерия Кочрена:
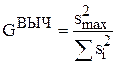 , (3.8)
, (3.8)
где 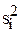 – точечные дисперсии, вычисляемые по формуле (3.6);
– точечные дисперсии, вычисляемые по формуле (3.6); 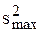 – максимальная из
– максимальная из 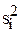 . Если GВЫЧ < GТАБЛ (a, N, L – 1), то гипотеза о постоянстве значения s2 признается верной.
. Если GВЫЧ < GТАБЛ (a, N, L – 1), то гипотеза о постоянстве значения s2 признается верной.
С помощью 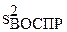 можно также проверить значимость коэффициентов модели без предположения об ее адекватности. Для этого также используется критерий Стьюдента, но формула другая:
можно также проверить значимость коэффициентов модели без предположения об ее адекватности. Для этого также используется критерий Стьюдента, но формула другая:
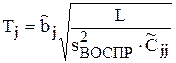 (3.9)
(3.9)
с числом степеней свободы n = N(L – 1), где 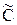 = (ФT Ф)–1 и двухсторонней критической областью.
= (ФT Ф)–1 и двухсторонней критической областью.
Замечание. Все приведенные положения основаны на предположении, что число параллельных опытов одинаково во всех экспериментальных точках. Если это предположение не выполняется, то расчетные формулы существенно усложнятся, а критерий Кочрена неприменим.
Тема 4. Планирование экспериментов
4.1. Задача планирования
Пример 4.1. Пусть объект имеет один входной параметр х. На рис. 4.1 цифрой 1 обозначена прямая, соответствующая истинной зависимости выхода от входа. Предположим, что в точках х1 и х2, расположенных вблизи средины области определения входного параметра, проведены эксперименты, но, вследствие ошибок, результаты, – точки у1 и у2, не лежат на линии 1. Построив по экспериментальным точкам уравнение эмпирической зависимости, получим прямую 2, которая, как видно на рисунке, значительно отличается от истинной зависимости.
Пусть теперь эксперименты проведены в точках х3 и х4, расположенных по краям области определения входного параметра, с такой же величиной ошибок. По полученным точкам у3 и у4 построена зависимость, соответствующая прямой 3, которая, как видно из рисунка, значительно ближе к истинной линии, чем прямая 2.
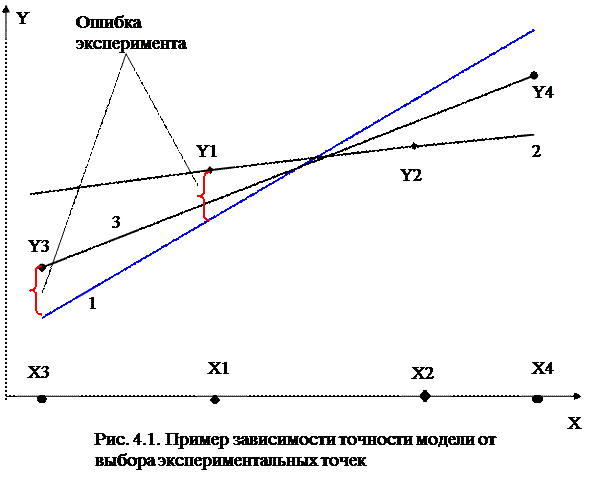 |
Задача планирования эксперимента: осуществить рациональный выбор экспериментальных точек и за счёт этого повысить точность создаваемой модели.
Применение методов планирования экспериментов предполагает возможность проведения опытов в заданных исследователем условиях, т.е. активных экспериментов.
4.2. Оптимальные планы эксперимента
Def. Пусть Wх – область возможных значений входных параметров объекта, которую назовем областью планирования. Планом эксперимента называется некоторое подмножество Р(Wх) Ì Wх точек, в которых проводятся эксперименты. Обычно план задается матрицей значений входных параметров в экспериментальных точках Х=[ 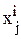 ] – матрицей планирования, i =1,…N, j = 1,…, m.
] – матрицей планирования, i =1,…N, j = 1,…, m.
Рассмотрим два оптимизационных свойства планов эксперимента – D- и G-оптимальность.
Def. План называется D-оптимальным, если его точки расположены так на Wх, что достигается max det(ФТФ) (или, что то же самое, – min det (ФТФ) –1).
Величина определителя матрицы С = s2(ФТФ)–1 характеризует “объем” эллипсоида рассеяния МНК-оценок, а, следовательно, является обобщенной характеристикой дисперсий МНК-оценок. Поэтому свойство D-оптимальности плана экспериментов эквивалентно свойству устойчивости оценок коэффициентов модели (3.1), их близости к истинным значениям коэффициентов.
Def. План называется G-оптимальным, если его точки расположены так, что достигается минимум максимального по хÎWх значения дисперсии прогноза D[ 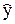 (x)].
(x)].
Поясним данное определение. Пусть имеем два плана Р1 и Р2. У первого плана дисперсия прогноза достигает максимума в некоторой точке х1 и равна в ней d1, а у второго плана дисперсия прогноза достигает максимума d2 в точке х2. Пусть d1 > d2 . Это значит, что по критерию G-оптимальности второй план лучше.
Для того, чтобы свойства D- и G-оптимальности не зависели от количества проведенных экспериментов, а зависели только от выбранных точек, используется нормированная дисперсионная матрица МНК-оценок: N×(ФТФ) –1 и, соответственно, нормированная дисперсия прогноза:
d(x) = N f(x)Т(ФТФ) –1 f(x). (4.1)
Обозначим dmax = max{d(x) | xÎ Wх} – максимальное значение нормированной дисперсии прогноза. Согласно определению, значение dmax должно быть минимальным, если план Р(Wх) является G-оптимальным. Имеют место следующие свойства.
Теорема 4.1 (об эквивалентности оптимальных планов). Для любого плана следующие утверждения эквивалентны.
1) План является D-оптимальным.
2) План является G-оптимальным.
3) dmax = k, где k – число коэффициентов модели (1.3).
Эквивалентность пунктов 1) и 2) означает, что любой D-оптимальный план экспериментов является одновременно и G-оптимальным и наоборот. Пункт 3) указывает простой способ проверки качества любого плана по величине d = (dmax – k) / k. Для D- и G-оптимальных планов d = 0, для прочих планов d > 0.
Теорема 4.2 (об инвариантности D-оптимального плана). D-оптимальный план инвариантен относительно любого невырожденного линейного преобразования базисных функций fj(x).
Пример 4.2. (Разобрать самим). Пусть даны результаты двух серий экспериментов над одним и тем же объектом, представленные регрессионными матрицами F1 и F2 модели у = b + a x и векторами у1 и у2 значений выхода.
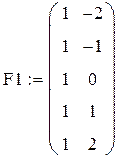
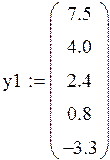
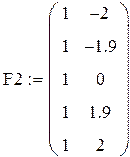
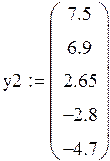
|
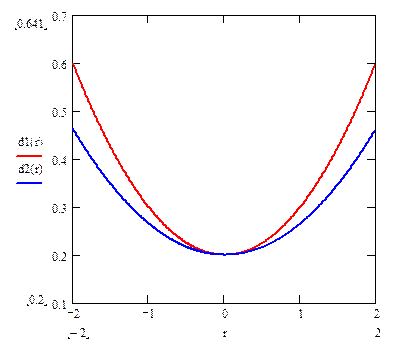
Заметим, что экспериментальные точки второй серии сдвинуты к концам интервала [–2, +2]. Величина остаточной дисперсии в обеих сериях составляет 0,681 ед2, т.е. экспериментальная ошибка в среднем одинакова. Однако, дисперсия прогноза, как несложно проверить различна. В первой серии d(x) = 0.1x2 + 0.2 во второй – d(x) = 0.0657x2 + 0.2, т.е. ее максимальное значение, достигаемое в точке х = ±2, во второй серии меньше на 22,9%. Графики обеих зависимостей – на рис. 4.2.
Несложно проверить, что оба плана не являются D-оптимальными, поскольку максимальная величина нормированной дисперсии прогноза N×d(x) составляет в первой серии – 3, во второй – 2.314, в то время, как у D-оптимального плана она должна равняться 2.
4.3. D-оптимальные и близкие к ним планы на гиперкубе
Достижение возможно большей точности модели связано с оптимальным использованием области планирования Wх при проведении экспериментов. Поэтому при использовании критериев D- или G-оптимальности вид области планирования является очень важным условием задачи и произвольное изменение ее конфигурации приводит к существенному изменению оптимального плана.
Будем считать, что областью значений входных параметров объекта является гиперкуб: Wх = [ –1, +1] m, т.е. хjÎ[ –1, +1], j = 1,…m. Для произвольного отрезка [ 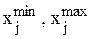 ] легко найти замену переменных, переводящую его в [ –1, +1]:
] легко найти замену переменных, переводящую его в [ –1, +1]:
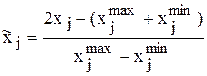 .
.
Согласно теореме 5.4 об инвариантности, после такой замены план останется D-оптимальным.
Полный факторный план (ПФП) – это план, в котором каждый входной параметр принимает два значения: +1 и –1 и при этом перебираются все возможные комбинации. Число строк в матрице Х равно N =2m. Рассмотрим основные свойства ПФП.
1. Столбцы матрицы Ф для линейной y = b0 + b1x1 +…+ bmxm и неполной квадратичной
y = b0 + b1x1 +…+ bmxm + b12 x1 x2 + b13 x1 x3 + … + bm –1, m xm –1 xm
моделей в ПФП ортогональны, а, следовательно, матрица ФТФ диагональна и равна N×Ik.
Свойство легко проверяется.
2. Для линейной и неполной квадратичной моделей ПФП является D-оптимальным.
Доказательство. Докажем для линейной модели: f(x) = [1, x1 ,… xm]T, k = m + 1. Согласно свойству 1, (ФТФ)–1 = (1/ N) Im +1. Следовательно
d(x) = N f(x)Т(ФТФ) –1 f(x) = f(x)Т Im +1 f(x) = 1 + 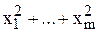 .
.
Поскольку хjÎ[–1, +1], то максимум d(x) достигается при хj = ± 1 и равен m + 1, т.е. числу k коэффициентов модели. Следовательно, по теореме 5.3, ПФП D-оптимален.
Оптимальные планы для квадратичной модели. (Разобрать самим). Полная квадратичная модель с m входными параметрами имеет вид
y = b0 + b1x1 +…+ bmxm + b12x1x2 + b13x1x3 + … + bm –1, m xm–1xm +
+ 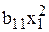 +…+
+…+ 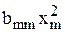 .
.
Модель содержит k = 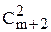 = (m + 2)(m + 1) / 2 коэффициентов. Для получения МНК-оценок каждый входной параметр в экспериментах должен принимать значения, как минимум, на трех различных уровнях, иначе матрица ФТФ будет вырожденной.
= (m + 2)(m + 1) / 2 коэффициентов. Для получения МНК-оценок каждый входной параметр в экспериментах должен принимать значения, как минимум, на трех различных уровнях, иначе матрица ФТФ будет вырожденной.
Доказано, что D-оптимальный план для квадратичной модели должен содержать дробное число L параллельных опытов, поэтому реальных в точности D-оптимальных планов для таких моделей не существует. На практике применяются различные планы, близкие по характеристикам к D-оптимальным. Наиболее подходящими являются так называемые планы типа В m, где m – число входных параметров модели. Они содержат точки ПФП, плюс центры (m – 1)-мерных граней гиперкуба, т.е. точки с координатами (±1, 0,…, 0). Всего план Вm, содержит N = 2m + 2m точек. Ниже приведена матрица плана В2.
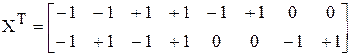 .
.
В таблице 4.1 приведены сравнительные характеристики планов Вm и D-оптимальных при различных значениях m.
| Таблица 4.1 | |||||
| Характеристики планов Вm | |||||
| m | 2 | 3 | 4 | 5 | |
| dmax | Вm | 10 | 11.2 | 18.5 | 34.2 |
| D-оптим. | 6 | 10 | 15 | 21 | |
| N | 8 | 14 | 24 | 42 | |
Дата: 2019-02-25, просмотров: 397.