Раздел 3. Статистическое моделирование
Литература
1. Андерсон, Т. Введение в многомерный статистический анализ [Текст] / Т. Андерсон / Пер. с англ. М.: Физматгиз, 1963. 500 с.
2. Айвазян, С. А. Прикладная статистика и основы эконометрики. Учебник для вузов [Текст] / С.А. Айвазян, В.С. Мхитарян. М.: ЮНИТИ, 1998,1022 с.
3. Демиденко, Е. З. Линейная и нелинейная регрессии [Текст] / Е. З. Демиденко. М.: Финансы и статистика, 1981. 302 с.
4. Дрейпер, Н. Прикладной регрессионный анализ. [Текст] / Н. Дрейпер, Г. Смит. М.: Статистика, 1973.
5. Леман, Э. Проверка статистических гипотез. [Текст] / Э. Леман. М.: Наука, 1979.
6. Магнус, Я. Р. Эконометрика. Начальный курс. Учебное пособие. [Текст] / Я.Р. Магнус, П. К. Катышев, А. А. Пересецкий // М.: Дело, 1998, 248 с.
7. Сысоев, В. В. Парная линейная регрессия. [Компьют] / В. В. Сысоев. Воронеж, 2002.
8. Хартман, К. Планирование экспериментов в исследовании технологических процессов [Текст] / К. Хартман, Э. Лецкий, В. Шеффер / Пер. с нем. М.: Мир, 1977. 552 с.
Введение. Что такое статистическое моделирование
Напомним, что эмпирические модели получаются в результате математической обработки данных экспериментов.
Статистическое моделирование – процесс построения эмпирической модели объекта, который имеет следующие особенности.
1) Любой объект моделирования представляется в виде «черного ящика», т. е. системы, в которой исследователю известны только водные данные и выходные, а внутренняя структура объекта неизвестна.
2) Применяется статистический подход – т. е. происходит наблюдение и обработка большого числа экспериментов (в каждом эксперименте происходят ошибки, но при большом количестве экспериментов можно уловить важные закономерности, исследуя какую-нибудь усредненную величину)

| ||||
| ||||
|
|
 |  |
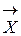 – набор (вектор) контролируемых входных параметров;
– набор (вектор) контролируемых входных параметров;
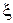 – неконтролируемые входные параметры (случайные помехи);
– неконтролируемые входные параметры (случайные помехи);
Y– выходной параметр.
3) Любые сделанные выводы и их последствия имеют вероятностный характер. Иными словами, после проведения исследований объекта средствами статистического моделирования, должны делаться какие-выводы о свойствах объекта. Их особенность состоит в том, что они в принципе не могут быть верными со 100%-й гарантией, всегда существует малая вероятность их ошибочности.
Тема 1. Основные понятия теории вероятностей и математической
Статистики
Случайные векторы и их характеристики
Основные понятия.
Def . Случайным вектором 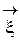 называется вектор, координатами которого являются случайные величины:
называется вектор, координатами которого являются случайные величины: 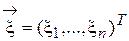 .
.
Набор (x1,…, xn) называют также системой случайных величин. Как и обычные (скалярные) случайные величины, случайные векторы бывают непрерывными и дискретными.
Исчерпывающей вероятностной характеристикой случайного вектора является его функция распределения (функция совместного распределения системы случайных величин).
Def . Функция распределения F(x1,…, xn) случайного вектора 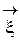 равна вероятности следующего сложного события: {( x1< x1) Ù … Ù ( xn< xn)}.
равна вероятности следующего сложного события: {( x1< x1) Ù … Ù ( xn< xn)}.
Def. Плотностью совместного распределения системы случайных величин (плотностью распределения случайного вектора) называется функция
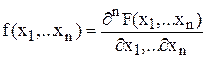 .
.
Имеет место также следующая формула
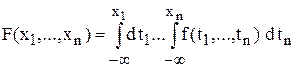 .
.
Пусть D Ì E n – некоторая область n-мерного пространства. Тогда вероятность попадания случайного вектора в область D равна следующему n-кратному интегралу:
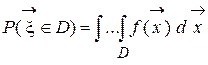 .
.
Например, для одномерной случайной величины Р(xÎ[a, b]) = 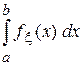 , а при а = – ¥ будет Р(xÎ[– ¥, b]) = Р(x < b) = Fx (b).
, а при а = – ¥ будет Р(xÎ[– ¥, b]) = Р(x < b) = Fx (b).
Доказательство.
1) Распишем произвольную i-ю компоненту вектора h:
hi = a i1×x1 + a i 2×x2 +… + a i n×xn.
Согласно известному свойству математического ожидания:
M[hi]=M[a i1×x1 + a i2×x2 +… + a in×xn] = a i1×M[x1] + a i2×M[x2] +… + a in×M[xn].
Т.е. для получения M[hi] надо i-ю строку матрицы А умножить на вектор M[ 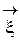 ], а если умножить на M[
], а если умножить на M[ 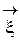 ] всю матрицу А, то получим M[
] всю матрицу А, то получим M[ 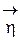 ]. Ч.Т.Д.
]. Ч.Т.Д.
2). По определению D[h] = M [(h – Mh) (h – Mh)T].
В силу 1) h – Mh = Ax – A Mx = A(x – Mx). Следовательно
D[h] = M [А (x – Mx) (x – Mx)T АТ] = A M [(x – Mx) (x – Mx)T] АТ = A D[x] АТ, что и требовалось доказать.
Основные понятия математической статистики.
Статистические оценки
Задача математической статистики состоит в разработке методов сбора и обработки статистических данных для получения научных и практических выводов.
Пусть x – некоторая случайная величина (СВ).
Def . Выборкой величины x объема N называют набор из N независимых СВ x1, … xN, распределенных также, как x.
Иными словами, выборка – это N независимых экземпляров СВ x.
Def . Реализацией выборки называется неслучайная совокупность  значений элементов выборки, полученных в результате эксперимента. (Т.е. в результате эксперимента каждая случайная величина xi получила некоторое значение, которое обозначается
значений элементов выборки, полученных в результате эксперимента. (Т.е. в результате эксперимента каждая случайная величина xi получила некоторое значение, которое обозначается 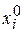 )
)
Def . Статистика – это некоторая функция выборки j( x1, … xN).
Def. Пусть q – некоторый параметр СВ x, Q – область его значений (qÎQ). Точечной статистической оценкой 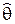 параметра q называется любая статистика
параметра q называется любая статистика 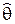 =
= 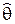 ( x1, … xN), принимающая значения из области Q.
( x1, … xN), принимающая значения из области Q.
Например, оценкой математического ожидания может быть любая статистика, имеющая ту же размерность, что и Х:
1) 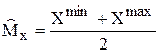 ; 2)
; 2) 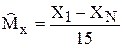 ;
;
3) 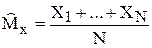 ; 4)
; 4) 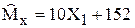 .
.
Свойства статистических оценок. Основное назначение статистических оценок – давать приближенное значение для оцениваемого параметра, найденное по реализации выборки. Для того, чтобы это приближение было “хорошим”, статистические оценки должны обладать определенными свойствами.
Пусть 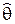 – статистическая оценка параметра q. Допустим, что по некоторой реализации выборки получено ее числовое значение
– статистическая оценка параметра q. Допустим, что по некоторой реализации выборки получено ее числовое значение 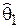 . Повторяя опыты, т.е. получая другие реализации выборки, мы сможем определить другие значения этой оценки –
. Повторяя опыты, т.е. получая другие реализации выборки, мы сможем определить другие значения этой оценки – 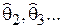 , которые, вообще говоря, между собой различны. Следовательно, статистическую оценку надо рассматривать как случайную величину, имеющую определенный закон распределения и числовые параметры – матожидание, дисперсию и т.д. (Этого следовало ожидать, т.к. оценка представляет собой некоторую функцию случайных величин – элементов выборки).
, которые, вообще говоря, между собой различны. Следовательно, статистическую оценку надо рассматривать как случайную величину, имеющую определенный закон распределения и числовые параметры – матожидание, дисперсию и т.д. (Этого следовало ожидать, т.к. оценка представляет собой некоторую функцию случайных величин – элементов выборки).
Представим себе, что некоторая оценка постоянно дает значение параметра с избытком, например это оценка 4). Ясно, что в этом случае и математическое ожидание такой оценки (как случайной величины) будет больше истинного значения параметра. Использование такой оценки привело бы к систематическим (одного знака) ошибкам. Поэтому естественно потребовать, чтобы математическое ожидание статистической оценки было равно истинному значению оцениваемого параметра, т.е. 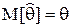 .
.
Def. Статистическая оценка, математическое ожидание которой равно истинному значению оцениваемого параметра, называется несмещенной.
Однако, было бы ошибочным считать, что несмещенная оценка всегда дает хорошее приближение оцениваемого параметра. Например, значения 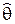 могут быть сильно рассеяны вокруг своего среднего значения, т.е. дисперсия D[
могут быть сильно рассеяны вокруг своего среднего значения, т.е. дисперсия D[ 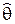 ] может быть значительной. В этом случае найденная по данным одной выборки оценка может оказаться весьма удаленной от своего среднего значения, а значит, и от самого оцениваемого параметра q. Если же потребовать, чтобы дисперсия D[
] может быть значительной. В этом случае найденная по данным одной выборки оценка может оказаться весьма удаленной от своего среднего значения, а значит, и от самого оцениваемого параметра q. Если же потребовать, чтобы дисперсия D[ 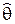 ] была малой, то возможность допустить большую ошибку оценивания исключена. По этой причине к статистической оценке предъявляется требование эффективности.
] была малой, то возможность допустить большую ошибку оценивания исключена. По этой причине к статистической оценке предъявляется требование эффективности.
Def . Эффективной называют статистическую оценку, которая при заданном объеме выборки N имеет наименьшую возможную дисперсию.
При рассмотрении выборок большого объема к статистическим оценкам предъявляют требование состоятельности.
Def . Состоятельной называют статистическую оценку, которая при N ® ¥ стремится по вероятности к оцениваемому параметру.
Характер такой сходимости может быть различным. Например, простая (слабая) состоятельность опирается на понятие сходимости случайных величин по вероятности:
P{ | xn – x | > e} ® 0 при n ® ¥.
Существуют также и другие понятия состоятельности: сильная, состоятельность в среднем и др.
Помимо перечисленных свойств статистических оценок, характеризующих качество приближения к истинному значению параметра, есть другие свойства, например, определяющие класс вычислительных формул для нахождения оценки. Одним из наиболее важных таких классов является класс линейных оценок, имеющих вид 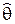 = а1 Х1 + … + а N Х N, где а j – заданные числа.
= а1 Х1 + … + а N Х N, где а j – заданные числа.
Примеры статистических оценок. Рассмотрим несколько важных примеров статистических оценок.
1. Оценка
 = (x1 + … + xN) / N – (1.2)
= (x1 + … + xN) / N – (1.2)
оценка математического ожидания. Имеют место следующие свойства.
Теорема 1.3 (о свойствах оценки  ).
).
1. Оценка  является
является
а) несмещенной;
б) эффективной в классе линейных несмещенных оценок;
2. Для дисперсии 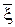 справедлива формула: D[
справедлива формула: D[  ] = D[x] / N.
] = D[x] / N.
Доказательство. Докажем свойство 1.а). Найдём M[  ]:
]:
M[  ] = (M[x1] + … + M[xN ]) / N = N× M[x] / N = M[x].
] = (M[x1] + … + M[xN ]) / N = N× M[x] / N = M[x].
Предпоследнее равенство вытекает из свойства выборки – каждый её элемент распределён как исходная СВ x.
Докажем свойство 2. Найдём D[ 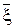 ]:
]:
D[ 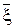 ] = (D[x1] + … + D[xN ]) / N 2 = N× D[x] / N 2 = D[x]/ N.
] = (D[x1] + … + D[xN ]) / N 2 = N× D[x] / N 2 = D[x]/ N.
Задание. Доказать свойства 1 а) и 2, используя теорему 1.2 о линейно зависимых случайных векторах, положив h = 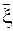 .
.
2. Оценка 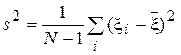 – оценка дисперсии.
– оценка дисперсии.
Теорема 1.4 (о свойствах s2). Оценка s2 является
а) несмещенной;
б) эффективной при нормальном распределении СВ x.
Остаточная дисперсия
Def. Остаточной дисперсией уравнения регрессии называется величина
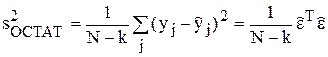 =
= 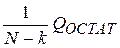
равная среднему квадрату отклонения экспериментальных данных от расчетных (k – число коэффициентов модели (1.3)).
Теорема 1.6 (о несмещенногсти остаточной дисперсии). Если выполнены условия теоремы Гаусса-Маркова, то остаточная дисперсия является несмещенной оценкой параметра s2.
Следствие. 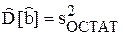 (ФTФ)–1 – несмещенная оценка.
(ФTФ)–1 – несмещенная оценка.
Значение остаточной дисперсии позволяет оценить точность построенного уравнения. Из нескольких альтернативных вариантов модели при прочих равных условиях предпочтение следует отдавать уравнению, имеющему наименьшую остаточную дисперсию.
МНК-прогноз. Пусть х – фиксированный вектор входных параметров. С помощью модели  (х) =
(х) = 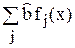 можно предсказать каким в среднем будет значение выходного параметра у при входе х, т.е.
можно предсказать каким в среднем будет значение выходного параметра у при входе х, т.е.  (х) – прогноз выхода при заданном входе. Так как МНК-оценки – случайные величины, то
(х) – прогноз выхода при заданном входе. Так как МНК-оценки – случайные величины, то  (х) – тоже случайная величина, как и всякая статистическая оценка. Её дисперсия характеризует среднюю точность прогноза. Найдем D[
(х) – тоже случайная величина, как и всякая статистическая оценка. Её дисперсия характеризует среднюю точность прогноза. Найдем D[  (х)] и ее оценку.
(х)] и ее оценку.
Обозначим f(x) = [f1(x),…, fk(x)]Т – вектор базисных функций. Тогда 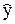 (х) = fT(x)
(х) = fT(x) 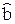 . Воспользуемся теоремой 1.2 о линейно зависимых векторах
. Воспользуемся теоремой 1.2 о линейно зависимых векторах 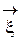 =
= 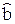 и
и 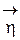 =
=  (х), положив в ней А = fT(x).
(х), положив в ней А = fT(x).
D[  (х)] = fT(x) D[
(х)] = fT(x) D[ 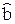 ] f(x) = s2 fT(x) (ФT Ф)–1f(x). (1.8)
] f(x) = s2 fT(x) (ФT Ф)–1f(x). (1.8)
Значит, согласно следствию из теоремы 3.1 об остаточной дисперсии
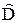 [
[  (х)] =
(х)] = 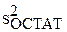 fT(x) (ФT Ф)–1f(x).
fT(x) (ФT Ф)–1f(x).
Теорема 3.2 (об МНК-прогнозе). Если выполнены условия теоремы Гаусса-Маркова, то прогноз  (х) является несмещённой эффективной оценкой в классе линейных по у несмещенных оценок.
(х) является несмещённой эффективной оценкой в классе линейных по у несмещенных оценок.
Доказательство. Линейность прогноза следует из линейности 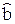 .
.
Докажем несмещенность. По теореме 1.2 имеем M[  (х)] = fT(x)M[
(х)] = fT(x)M[ 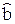 ] = = fT(x) b = M[y(x)] – несмещенная оценка.
] = = fT(x) b = M[y(x)] – несмещенная оценка.
Тема 2. Проверка статистических гипотез
Элементарные основы
Def. Статистическая гипотеза – некое суждение о свойствах случайной величины. Проверка статистической гипотезы – процедура сопоставления выбранной гипотезы с имеющимися экспериментальными данными, сопровождаемая количественной оценкой степени достоверности полученного вывода.
Пример 2.1. Согласно паспортным данным автомобильного двигателя, расход топлива на 100 км должен составить 10 л. Испытано 25 машин. Средний расход топлива составил 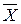 = 9.3 л. Известно, что расход топлива – СВ Х с известной дисперсией s2 = 4 л2. Проверить гипотезу: mx = 10 л.
= 9.3 л. Известно, что расход топлива – СВ Х с известной дисперсией s2 = 4 л2. Проверить гипотезу: mx = 10 л.
Обозначим Н0 – выдвигаемая гипотеза. Идея проверки состоит в вычислении по результатам эксперимента некоторой статистики К = К(Х1, …, ХN) – статистического критерия, обладающего следующим свойством: если гипотеза Н0 верна, то случайная величина К имеет строго определенный закон распределения. Чтобы проверить, справедлив ли в действительности этот закон, вся область V значений критерия К разбивается на две части: VКР – критическая область (область отклонения гипотезы) и V \ VКР – область принятия гипотезы.
Область VКР подбирается так, чтобы при предполагаемом законе распределения выполнялось равенство P(K Î VКР / Н0) = a, т.е. вероятность попадания К в VКР при верной гипотезе Н0 равна заданному числу a.
При малом значении a вступает в силу следующий принцип: маловероятное событие в единичном испытании практически невозможно. Практическим подтверждением справедливости этого принципа является игра «Русская рулетка».
Значит, если в результате эксперимента событие (K Î VКР) не выполнится, то гипотезу следует принять. В противном случае ее надо отвергнуть, т.к. при верной гипотезе данное событие практически невозможно, а если наступило – то гипотеза не верна.
Построение оптимальной критической области. При сформулированном подходе VКР не может быть определена однозначно, т.к. при любом законе распределения существует бесконечно много областей, вероятность попадания в которые равна заданному числу (см. рис. 2.1). Следовательно, метод нуждается в доработке. Для этого введем понятия ошибок I и II рода.
|
Def. Ошибка I рода состоит в отклонении верной гипотезы. Ошибка II рода состоит в принятии неверной гипотезы.
Чтобы понять разницу между этими понятиями – обратимся к примеру.
Пример 2.2. Система ПВО засекла летящий самолет. Гипотеза Н0 – самолет вражеский. В данном примере ошибка I рода состоит в том, что при верной гипотезе она была отвергнута, и вражеский самолет пропустили на свою территорию. Ошибка II рода – гипотеза была неверна, но её приняли, в результате чего был сбит свой самолет. Приведенный пример, в частности демонстрирует, что, как правило, цена ошибок I и II рода различна.
В принятых обозначениях PI = P(KÎVКР / Н0) = a – вероятность ошибки I рода; PII = P( KÎ(V \VКР) / 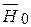 ) = b – вероятность ошибки II рода.
) = b – вероятность ошибки II рода.
Принцип оптимального выбора VКР состоит в следующем: при заданном уровне PI = a вероятность ошибки II рода должна быть минимальна (b ® min или 1– b® mах). Чтобы можно было оценить величину b, наряду с основной гипотезой Н0 выдвигают конкурирующую гипотезу Н1 = 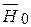 , отвергающую основную.
, отвергающую основную.
Вернёмся к примеру 2.1. При основной гипотезе Н0: mx = 10 л выдвинем конкурирующую, например Н1 : mx = 9 л. В качестве статистического критерия примем 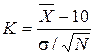 . При нормальном распределении СВ Х с параметрами mx = 10, D[X] = s2 , т.е. при верной гипотезе Н0, выбранный критерий К распределен нормально с параметрами mК = 0, D[K] = 1. Если же предположить, что верна гипотеза Н1, то случайная величина К имеет тоже нормальное распределение, но с параметрами D[K]=1,
. При нормальном распределении СВ Х с параметрами mx = 10, D[X] = s2 , т.е. при верной гипотезе Н0, выбранный критерий К распределен нормально с параметрами mК = 0, D[K] = 1. Если же предположить, что верна гипотеза Н1, то случайная величина К имеет тоже нормальное распределение, но с параметрами D[K]=1,
mК = 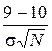 =
= 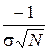 = –2,5. (2.1)
= –2,5. (2.1)
Обозначим VКР = [s, t ]. При заданном значении s величина t определяется из уравнения
P(KÎ[s, t ]) = a = U(t) – U(s), (2.2)
где U(х) 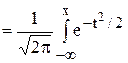 – функция Лапласа (функция нормального распределения или интеграл вероятности). Отсюда
– функция Лапласа (функция нормального распределения или интеграл вероятности). Отсюда
t = U(–1)[a + U(s)].
Иными словами, t является (a + U(s))- квантилем нормального распределения. В MathCad эта формула вычисления t имеет вид:
t:= qnorm(a + pnorm(s, 0, 1), 0, 1). (2.3)
Вероятность ошибки II рода равна
b = P( (KÏ VКР ) / H1 ) = P[KÎ( (–¥, s)  (t, +¥) )]= P[KÎ(–¥, s)] + P[KÎ(t, +¥)].
(t, +¥) )]= P[KÎ(–¥, s)] + P[KÎ(t, +¥)].
С учётом (2.1) значение b в MathCad вычисляется с помощью формулы
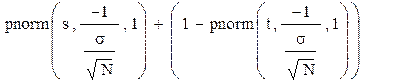 (2.4)
(2.4)
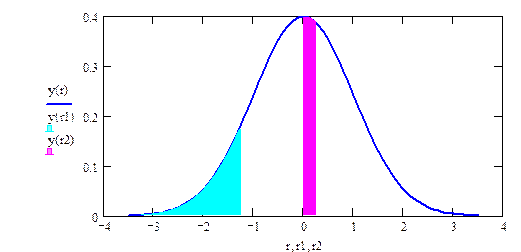
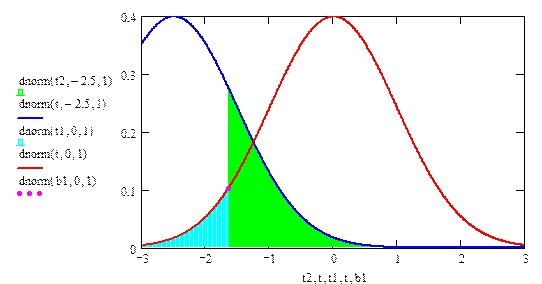
Теперь для нахождения оптимальной критической области надо определить значение s, при котором соблюдается условие (2.2) (т.е. (2.3)), а выражение (2.4) минимально. Несложно вычислить, что при a = 0.05 получим sopt = –¥, topt = – 1.64485, т.е. VКР = [–¥, –1.645]. Такая область называется левосторонней. При такой критической области b = 0.1962. На рис. 2.2 графически показаны значения a и b, найденные по формулам (2.2) и (2.4) при оптимальных границах критической области..
Def. Гипотеза вида q = b, где b – фиксированное число, называется простой.
При ней однозначно определяется распределение анализируемой СВ Х.
Def. Гипотеза вида q Î В, где В – фиксированное множество, называется сложной.
Например, гипотезы q < a, q ¹ a (а – число) – сложные.
Пусть в примере 2.1 основная гипотеза имеет вид mx = 10. Тогда при любой простой конкурирующей гипотезе mx = b, где b < 10, критическая область будет иметь ту же структуру, что и при конкурирующей гипотезе mx = 9. То есть будем иметь левостороннюю критическую область VКР = (– ¥, ta), где квантиль ta определяется из условия Р(К £ ta) = a. Следовательно, при сложной конкурирующей гипотезе mx < 10 критическая область будет такой же, см. рис. 2.3.
|
Соответственно, при сложной конкурирующей гипотезе mx >10 оптимальная критическая область будет правосторонней, т.е. VКР = ( t1– a, + ¥), где t1– a определяется из условия Р(К < t1– a) = 1 – a или Р(К ³ t1– a) = a. При a = 0.05 будет t1– a = 1.64485.
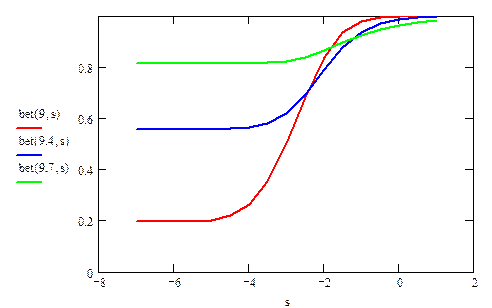


 Рис 2.3. Значение b(s) при различных простых конкурирующих гипотезах: – mХ = 9; – mХ = 9.4; – mХ = 9.7. Минимум везде достигается при s = – ¥
Рис 2.3. Значение b(s) при различных простых конкурирующих гипотезах: – mХ = 9; – mХ = 9.4; – mХ = 9.7. Минимум везде достигается при s = – ¥
Наконец, при сложной конкурирующей гипотезе mx ¹ 10 оптимальная критическая область будет двухсторонней, т.е.
VКР = (– ¥, ta/2) 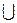 ( t1– a/2, + ¥),
( t1– a/2, + ¥),
где t1– a/2 определяется из условия Р( К ³ t1– a/2) = a/2 и Р( К < ta/2) = a/2. При a = 0.05 будет t1– a/2 = 1.95997 а ta/2 = –1.95997.
Раздел 3. Статистическое моделирование
Литература
1. Андерсон, Т. Введение в многомерный статистический анализ [Текст] / Т. Андерсон / Пер. с англ. М.: Физматгиз, 1963. 500 с.
2. Айвазян, С. А. Прикладная статистика и основы эконометрики. Учебник для вузов [Текст] / С.А. Айвазян, В.С. Мхитарян. М.: ЮНИТИ, 1998,1022 с.
3. Демиденко, Е. З. Линейная и нелинейная регрессии [Текст] / Е. З. Демиденко. М.: Финансы и статистика, 1981. 302 с.
4. Дрейпер, Н. Прикладной регрессионный анализ. [Текст] / Н. Дрейпер, Г. Смит. М.: Статистика, 1973.
5. Леман, Э. Проверка статистических гипотез. [Текст] / Э. Леман. М.: Наука, 1979.
6. Магнус, Я. Р. Эконометрика. Начальный курс. Учебное пособие. [Текст] / Я.Р. Магнус, П. К. Катышев, А. А. Пересецкий // М.: Дело, 1998, 248 с.
7. Сысоев, В. В. Парная линейная регрессия. [Компьют] / В. В. Сысоев. Воронеж, 2002.
8. Хартман, К. Планирование экспериментов в исследовании технологических процессов [Текст] / К. Хартман, Э. Лецкий, В. Шеффер / Пер. с нем. М.: Мир, 1977. 552 с.
Дата: 2019-02-25, просмотров: 333.