Уравнение регрессии – соотношение вида y = F(x), отражающее зависимость среднего значения выходного параметра объекта от значений входных параметров. Основу построения (синтеза) уравнения регрессии составляет метод наименьших квадратов.
Пример 1.3. Имеются экспериментальные данные (Таблица 1.1). Построить функцию, приблизительно отражающую зависимость у от х, т.е. уравнение регрессии.
| Таблица 1.1. | ||||||
| x i | –3 | –2.5 | –2 | –1.5 | –1 | –0.5 |
| y i | –1.92 | –1.45 | –0.57 | 0.62 | 0.88 | 2.03 |
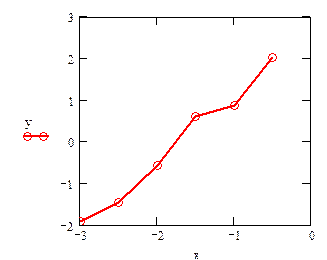
Если нанести точки на график и соединить их, то получим зигзагообразную линию, которая, впрочем, не слишком отличается от прямой (см. рис. 1.1). Неправильная форма графика объясняется, очевидно, ошибками, допущенными при получении данных. Из курса вычислительной математики нам известно, что в этом случае принято использовать среднеквадратичную аппроксимацию и метод наименьших квадратов (МНК). Аппроксимирующую функцию будем искать в классе многочленов первой степени, т.е. положим Y(x) = b1 x + b2.
|
Для идентификации (нахождения) этой зависимости надо найти статистические оценки  коэффициентов модели. Согласно МНК эти оценки находят из условия минимума функции
коэффициентов модели. Согласно МНК эти оценки находят из условия минимума функции
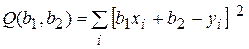 .
.
Для поиска минимума надо вычислить частные производные минимизируемой функции, приравнять их к 0 и решить полученную систему уравнения. В данном случае получим 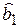 = 1.596;
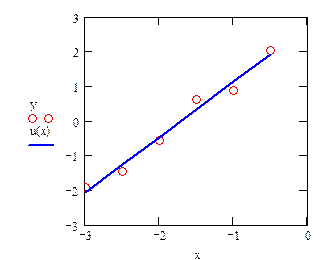
= 1.596; 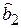 = 2.725, а аппроксимирующая функция примет вид Y(x) = 1.596 x + 2.725. На рис. 1.2 приведены графики исходных данных (точки) и аппроксимирующей функции (сплошная линия).
= 2.725, а аппроксимирующая функция примет вид Y(x) = 1.596 x + 2.725. На рис. 1.2 приведены графики исходных данных (точки) и аппроксимирующей функции (сплошная линия).
|
В более общем случае будем искать уравнение регрессии в виде функции, линейно зависящей от коэффициентов, т.е.
Y(x) = b1 f1(x) + … + bk fk(x), (1.3)
где f u(x) – заданные функции; b u – неизвестные коэффициенты. Для идентификации этой зависимости надо найти статистические оценки  коэффициентов модели. Согласно МНК эти оценки (МНК-оценки) находят из условия минимума функции
коэффициентов модели. Согласно МНК эти оценки (МНК-оценки) находят из условия минимума функции
Q(b) = 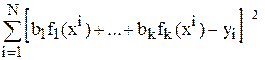 ,
,
где уi – наблюдаемое значение выходного параметра в i-м эксперименте.
Обозначим: Ф = [Фij] = [f j(x i)] – регрессионная (N ´ k)-матрица; b – вектор коэффициентов; у – вектор значений выхода. Тогда для вектора 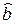 оценок коэффициентов имеем матричное уравнение
оценок коэффициентов имеем матричное уравнение
(ФT Ф) 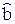 = ФT y. (1.4)
= ФT y. (1.4)
Если матрица (ФT Ф) не вырождена, то
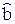 = (ФT Ф)–1 ФT y. (1.5)
= (ФT Ф)–1 ФT y. (1.5)
Теорема Гаусса-Маркова. Данная теорема формулирует основные свойства МНК-оценок и является теоретическим обоснованием МНК.
Теорема 1.5 (Гаусса-Маркова). Пусть выполнены следующие предположения.
1) Значение вектора у выходных параметров, полученного в результате серии экспериментов представляет собой сумму детерминированной и случайной составляющих:
у = уДЕТ(х) + уСЛУЧ(x) = у(х) + e,
где e – случайный N-мерный вектор с параметрами M[e] = 0; D[e] = s2I;
2) Матрица ФТФ не вырождена.
3) Существует вектор b истинных коэффициентов модели, такой что у(х) = Фb = M[y] – допущение об адекватности модели.
Тогда
1) МНК-оценка (1.5) является несмещенной оценкой вектора b истинных коэффициентов.
2) D[ 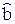 ] = s2 (ФT Ф)–1 – дисперсионная матрица вектора МНК-оценки.
] = s2 (ФT Ф)–1 – дисперсионная матрица вектора МНК-оценки.
Доказательство. 1) В силу предположения 2) матрица ФТФ не вырождена и имеет место формула (1.5). Из (1.5) и теоремы 1.2 п. 1) о линейно зависимых векторах имеем:
M [ 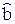 ] = M [(ФT Ф)–1 ФT y] = (ФT Ф)–1 ФT M [y].
] = M [(ФT Ф)–1 ФT y] = (ФT Ф)–1 ФT M [y].
Так как по условию М [у] = Фb, то
M [ 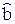 ] = (ФT Ф)–1 (ФTФ) b = b.
] = (ФT Ф)–1 (ФTФ) b = b.
Следовательно, M [ 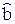 ] = b – оценка несмещенная.
] = b – оценка несмещенная.
2) Воспользуемся теоремой 1.2 п.2), положив 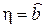 , x = y, A=(ФTФ)–1 ФT.
, x = y, A=(ФTФ)–1 ФT.
Тогда D [ 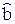 ] = (ФT Ф)–1 ФT D[y] ( (ФT Ф)–1 ФT)T.
] = (ФT Ф)–1 ФT D[y] ( (ФT Ф)–1 ФT)T.
По свойству дисперсии и по условию теоремы Гаусса-Маркова D[y] = D[e] = s2I. Далее, известны следующие свойства матриц (см. Практика п.1.1):
а) (B C)T = C T BT для любых В и С;
б) (ФTФ) и (ФTФ)–1 – симметричные матрицы (при транспонировании не меняются).
Значит
D [ 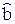 ] =s2 (ФT Ф)–1 ФT Ф (ФT Ф)–1 = s2 (ФT Ф)–1 Ф,
] =s2 (ФT Ф)–1 ФT Ф (ФT Ф)–1 = s2 (ФT Ф)–1 Ф,
что и требовалось доказать.
Обычно обозначают s2(ФT Ф)–1 = С – дисперсионная матрица МНК-оценок.
Дата: 2019-02-25, просмотров: 371.