Def. Если b_j = 0, то говорят, что МНК-оценка 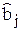 незначима.

Это означает, что член b_j ×f_j (x) не должен входить в модель (1.3).

Выдвинем гипотезу Н₀: b_j = 0 при альтернативной Н₁: b_j ¹ 0. Так как при верной Н₀ СВ 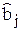 имеет нормальное распределение N(0, C_jj), где С = D[ 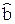] = = s² (Ф^T Ф)^–1 – ковариационная матрица МНК-оценок, а C_jj – её диагональный элемент,  то СВ Х =  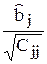имеет распределение N(0, 1).

Согласно теореме 3.1, статистика 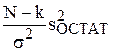имеет распределение c² с числом степеней свободы n = N – k и не зависит от 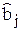. Это означает, что при верной Н₀ случайные величины

,  j = 1, …, k,                      (3.1)

где 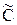= (Ф^TФ)^–1 , имеют распределение Стьюдента с числом степеней свободы n = N – k. При альтернативной гипотезе Н₁: b_j ¹ 0 критическая область имеет двухстороннюю структуру: если  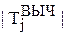> t_1–a./2, то основная гипотеза не верна и МНК-оценка  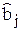значима.

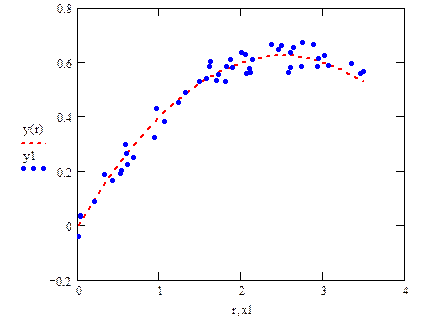
Рис. 3.1. Модель эффективна

Проверка эффективности регрессии. На объект исследования всегда воздействуют как контролируемые, так и неконтролируемые (помехи) входные параметры, причём степень их влияния может быть различной. Так, на рис. 3.1 изображена ситуация, когда влияние случайных помех относительно невелико, и мы можем построить модель процесса в виде уравнения регрессии, график которой изображён пунктиром.

Однако влияние помех может быть столь велико, что на их фоне воздействие контролируемых входных параметров не просматривается. Такой случай представлен на рис. 3.2. В этом случае единственной возможной моделью может быть зависимость вида y = b₀ = 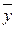 (см. пунктирная линия на рис. 3.2).

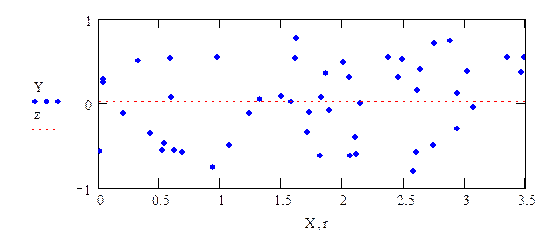
Рис. 3.2. Модель неэффективна

Дадим этим ситуациям формальное описание.

Пусть модель (1.3) содержит свободный член b₀. Предположим, что влияние на выходной параметр у контролируемых входных параметров х_i незначимо на фоне случайных помех. Этот факт можно сформулировать в виде статистической гипотезы Н₀: b_j = 0 " j ¹ 0. В отличие от предыдущего пункта, речь идет не об отдельных членах модели, а об уравнении в целом.

Def. Если гипотеза Н₀ верна, то будем говорить, что модель (1.3) неэффективна.

Это означает, что условие 3) теоремы Гаусса-Маркова принимает вид у(х) = b₀, а условие 1) вырождается в равенство у_i = b₀ + e.

При рассмотрении коэффициента детерминации мы показали, что если модель (1.3) содержит свободный член b₀, то имеет место равенство (1.7):

å(у_i – 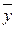)² = å(у_i – 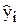) ² + å  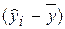² Þ Q_ОБЩ = Q_ОСТАТ + Q_РЕГР.

Теорема 3.2. Если eÎN(0, s² I), то при верной гипотезе о неэффективности модели (1.3) случайные величины Q_ОСТАТ /s² и Q_РЕГР /s² независимы и распределены по законам c²(N – k) и c² (k – 1), соответственно.

Это означает, что при верной гипотезе Н₀: b_j = 0 " j ¹0 статистика

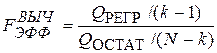                                  (3.2)

имеет распределение Фишера с числами степеней свободы k – 1 и N – k. Таким образом, для проверки эффективности модели (1.3) может быть использован статистический критерий (3.2) с правосторонней критической областью: если F^ВЫЧ > t_1–a то основная гипотеза не верна и модель (3.1) эффективна.