Def . Случайные величины называются независимыми, если закон распределения любой из них не зависит от того, какие значения приняли другие величины. В противном случае величины называются зависимыми.
В курсе математики изучаются величины, связанные функциональной зависимостью. Например, таковыми является площадь прямоугольника, его длина и ширина, связанные функциональной зависимостью вида s = a×h. Возрастание или убывание a или h неизбежно повлечёт возрастание s.
Зависимость случайных величин принципиально отличается от функциональной зависимости, поскольку возрастание одной величины не влечёт обязательного изменения другой. Например, рост и вес человека связаны между собой, т.к. при прочих равных условиях увеличение роста влечёт увеличение веса. Однако можно найти много пар людей, для которых эта зависимость не выполняется. В данном случае зависимость проявляется как тенденция, которая в большинстве случаев наблюдается, но возможны и исключения.

На графике отражены данные измерений роста (ось Х) и веса (ось Y) 20-ти здоровых мужчин (точки), а прямой изображена известная эмпирическая зависимость Y = X – 100. Как видим, индивидуальные данные отклоняются от прямой, но в целом тенденция наблюдается.
Теорема 1.1 (о независимости случайных величин). Для того, чтобы случайные величины x1,…, xn были независимы необходимо и достаточно, чтобы выполнялось равенство:
F(x1,…, xn) = F1(x1) ×…× Fn(xn),
где F1(x1) ,…, Fn(xn) – индивидуальные законы распределения случайных величин x1,…, xn.
Следствие. Для того чтобы случайные величины x1,…, xn были независимы необходимо и достаточно, чтобы выполнялось равенство:
f(x1,…, xn) = f1(x1) ×…× fn(xn),
где f1(x1) ,…, fn(xn) – индивидуальные плотности распределения случайных величин x1,…, xn.
Def. Математическим ожиданием случайного вектора 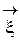 называется вектор
называется вектор 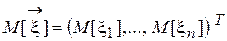 .
.
Def. Ковариацией случайных величин x1 и x2 называется величина
cov(x1, x2) = M [(x1 – M[x1] ) × (x2 – M[x2])].
При x1 = x2 ковариация x1 и x2 равна дисперсии x1, т.е. D[x1]. При x1 ¹ x2 ковариация x1 и x2 показывает тесноту связи x1 и x2. Если x1 и x2 независимы, то их ковариация равна нулю. Обратное, вообще говоря, неверно. Исключение составляет нормальное распределение, для которого следование верно в обе стороны.
Если при возрастании или убывании одной из xi и другая величина ведет себя аналогично (т.е. возрастает или убывает вместе с первой величиной), то cov(x1, x2) > 0. Если же возрастание одной величины сопровождается убыванием другой, то cov(x1, x2) < 0. Для любых x1 и x2 справедливо неравенство
0 £ |cov(x1, x2)| £  .
.
Def . Ковариационной (дисперсионной) матрицей случайного вектора 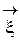 называется матрица D[
называется матрица D[ 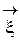 ], элементы которой Di j равны cov(xi, xj).
], элементы которой Di j равны cov(xi, xj).
Имеет место матричное представление:
D[ 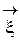 ] = M [ (
] = M [ ( 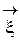 – M[
– M[ 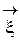 ] ) × (
] ) × ( 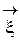 – M[
– M[ 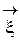 ] )T ]. (1.1)
] )T ]. (1.1)
Пояснение. Напомним, что если х и у – некоторые векторы, то произведение хТ у является скаляром (скалярное произведение векторов), а х уТ– матрицей В, состоящей из элементов Вij = хi ×уj. Поэтому в результате перемножения в формуле (1.1) получается матрица.
Одна важная теорема. В статистическом моделировании большое значение имеет следующая теорема.
Теорема 1.2 (о линейно зависимых случайных векторах). Пусть между случайными векторами 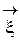 и
и 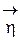 имеет место линейная функциональная зависимость h = Аx, где А – некоторая прямоугольная матрица (m строк и n столбцов). Тогда
имеет место линейная функциональная зависимость h = Аx, где А – некоторая прямоугольная матрица (m строк и n столбцов). Тогда
1) M[h] = A × M[x];
2) D[h] = A D[x] AT.
Доказательство.
1) Распишем произвольную i-ю компоненту вектора h:
hi = a i1×x1 + a i 2×x2 +… + a i n×xn.
Согласно известному свойству математического ожидания:
M[hi]=M[a i1×x1 + a i2×x2 +… + a in×xn] = a i1×M[x1] + a i2×M[x2] +… + a in×M[xn].
Т.е. для получения M[hi] надо i-ю строку матрицы А умножить на вектор M[ 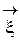 ], а если умножить на M[
], а если умножить на M[ 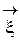 ] всю матрицу А, то получим M[
] всю матрицу А, то получим M[ 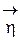 ]. Ч.Т.Д.
]. Ч.Т.Д.
2). По определению D[h] = M [(h – Mh) (h – Mh)T].
В силу 1) h – Mh = Ax – A Mx = A(x – Mx). Следовательно
D[h] = M [А (x – Mx) (x – Mx)T АТ] = A M [(x – Mx) (x – Mx)T] АТ = A D[x] АТ, что и требовалось доказать.
Основные понятия математической статистики.
Статистические оценки
Задача математической статистики состоит в разработке методов сбора и обработки статистических данных для получения научных и практических выводов.
Пусть x – некоторая случайная величина (СВ).
Def . Выборкой величины x объема N называют набор из N независимых СВ x1, … xN, распределенных также, как x.
Иными словами, выборка – это N независимых экземпляров СВ x.
Def . Реализацией выборки называется неслучайная совокупность  значений элементов выборки, полученных в результате эксперимента. (Т.е. в результате эксперимента каждая случайная величина xi получила некоторое значение, которое обозначается
значений элементов выборки, полученных в результате эксперимента. (Т.е. в результате эксперимента каждая случайная величина xi получила некоторое значение, которое обозначается 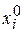 )
)
Def . Статистика – это некоторая функция выборки j( x1, … xN).
Def. Пусть q – некоторый параметр СВ x, Q – область его значений (qÎQ). Точечной статистической оценкой 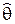 параметра q называется любая статистика
параметра q называется любая статистика 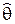 =
= 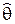 ( x1, … xN), принимающая значения из области Q.
( x1, … xN), принимающая значения из области Q.
Например, оценкой математического ожидания может быть любая статистика, имеющая ту же размерность, что и Х:
1) 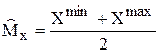 ; 2)
; 2) 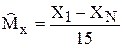 ;
;
3) 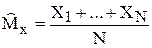 ; 4)
; 4) 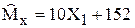 .
.
Свойства статистических оценок. Основное назначение статистических оценок – давать приближенное значение для оцениваемого параметра, найденное по реализации выборки. Для того, чтобы это приближение было “хорошим”, статистические оценки должны обладать определенными свойствами.
Пусть 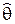 – статистическая оценка параметра q. Допустим, что по некоторой реализации выборки получено ее числовое значение
– статистическая оценка параметра q. Допустим, что по некоторой реализации выборки получено ее числовое значение 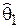 . Повторяя опыты, т.е. получая другие реализации выборки, мы сможем определить другие значения этой оценки –
. Повторяя опыты, т.е. получая другие реализации выборки, мы сможем определить другие значения этой оценки – 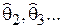 , которые, вообще говоря, между собой различны. Следовательно, статистическую оценку надо рассматривать как случайную величину, имеющую определенный закон распределения и числовые параметры – матожидание, дисперсию и т.д. (Этого следовало ожидать, т.к. оценка представляет собой некоторую функцию случайных величин – элементов выборки).
, которые, вообще говоря, между собой различны. Следовательно, статистическую оценку надо рассматривать как случайную величину, имеющую определенный закон распределения и числовые параметры – матожидание, дисперсию и т.д. (Этого следовало ожидать, т.к. оценка представляет собой некоторую функцию случайных величин – элементов выборки).
Представим себе, что некоторая оценка постоянно дает значение параметра с избытком, например это оценка 4). Ясно, что в этом случае и математическое ожидание такой оценки (как случайной величины) будет больше истинного значения параметра. Использование такой оценки привело бы к систематическим (одного знака) ошибкам. Поэтому естественно потребовать, чтобы математическое ожидание статистической оценки было равно истинному значению оцениваемого параметра, т.е. 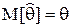 .
.
Def. Статистическая оценка, математическое ожидание которой равно истинному значению оцениваемого параметра, называется несмещенной.
Однако, было бы ошибочным считать, что несмещенная оценка всегда дает хорошее приближение оцениваемого параметра. Например, значения 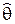 могут быть сильно рассеяны вокруг своего среднего значения, т.е. дисперсия D[
могут быть сильно рассеяны вокруг своего среднего значения, т.е. дисперсия D[ 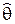 ] может быть значительной. В этом случае найденная по данным одной выборки оценка может оказаться весьма удаленной от своего среднего значения, а значит, и от самого оцениваемого параметра q. Если же потребовать, чтобы дисперсия D[
] может быть значительной. В этом случае найденная по данным одной выборки оценка может оказаться весьма удаленной от своего среднего значения, а значит, и от самого оцениваемого параметра q. Если же потребовать, чтобы дисперсия D[ 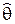 ] была малой, то возможность допустить большую ошибку оценивания исключена. По этой причине к статистической оценке предъявляется требование эффективности.
] была малой, то возможность допустить большую ошибку оценивания исключена. По этой причине к статистической оценке предъявляется требование эффективности.
Def . Эффективной называют статистическую оценку, которая при заданном объеме выборки N имеет наименьшую возможную дисперсию.
При рассмотрении выборок большого объема к статистическим оценкам предъявляют требование состоятельности.
Def . Состоятельной называют статистическую оценку, которая при N ® ¥ стремится по вероятности к оцениваемому параметру.
Характер такой сходимости может быть различным. Например, простая (слабая) состоятельность опирается на понятие сходимости случайных величин по вероятности:
P{ | xn – x | > e} ® 0 при n ® ¥.
Существуют также и другие понятия состоятельности: сильная, состоятельность в среднем и др.
Помимо перечисленных свойств статистических оценок, характеризующих качество приближения к истинному значению параметра, есть другие свойства, например, определяющие класс вычислительных формул для нахождения оценки. Одним из наиболее важных таких классов является класс линейных оценок, имеющих вид 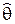 = а1 Х1 + … + а N Х N, где а j – заданные числа.
= а1 Х1 + … + а N Х N, где а j – заданные числа.
Примеры статистических оценок. Рассмотрим несколько важных примеров статистических оценок.
1. Оценка
 = (x1 + … + xN) / N – (1.2)
= (x1 + … + xN) / N – (1.2)
оценка математического ожидания. Имеют место следующие свойства.
Теорема 1.3 (о свойствах оценки  ).
).
1. Оценка  является
является
а) несмещенной;
б) эффективной в классе линейных несмещенных оценок;
2. Для дисперсии 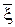 справедлива формула: D[
справедлива формула: D[  ] = D[x] / N.
] = D[x] / N.
Доказательство. Докажем свойство 1.а). Найдём M[  ]:
]:
M[  ] = (M[x1] + … + M[xN ]) / N = N× M[x] / N = M[x].
] = (M[x1] + … + M[xN ]) / N = N× M[x] / N = M[x].
Предпоследнее равенство вытекает из свойства выборки – каждый её элемент распределён как исходная СВ x.
Докажем свойство 2. Найдём D[ 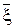 ]:
]:
D[ 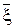 ] = (D[x1] + … + D[xN ]) / N 2 = N× D[x] / N 2 = D[x]/ N.
] = (D[x1] + … + D[xN ]) / N 2 = N× D[x] / N 2 = D[x]/ N.
Задание. Доказать свойства 1 а) и 2, используя теорему 1.2 о линейно зависимых случайных векторах, положив h = 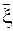 .
.
2. Оценка 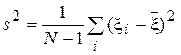 – оценка дисперсии.
– оценка дисперсии.
Теорема 1.4 (о свойствах s2). Оценка s2 является
а) несмещенной;
б) эффективной при нормальном распределении СВ x.
Дата: 2019-02-25, просмотров: 408.