Элементарные основы

Def. Статистическая гипотеза – некое суждение о свойствах случайной величины. Проверка статистической гипотезы – процедура сопоставления выбранной гипотезы с имеющимися экспериментальными данными, сопровождаемая количественной оценкой степени достоверности полученного вывода.

Пример 2.1. Согласно паспортным данным автомобильного двигателя, расход топлива на 100 км должен составить 10 л. Испытано 25 машин. Средний расход топлива составил 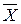= 9.3 л. Известно, что расход топлива – СВ Х с известной дисперсией s² = 4 л². Проверить гипотезу: m_x = 10 л.

Обозначим Н₀ – выдвигаемая гипотеза. Идея проверки состоит в вычислении по результатам эксперимента некоторой статистики К = К(Х₁, …, Х_N) – статистического критерия, обладающего следующим свойством: если гипотеза Н₀ верна, то случайная величина К имеет строго определенный закон распределения. Чтобы проверить, справедлив ли в действительности этот закон, вся область V значений критерия К разбивается на две части: V_КР – критическая область (область отклонения гипотезы) и V \ V_КР – область принятия гипотезы.

Область V_КР подбирается так, чтобы при предполагаемом законе распределения выполнялось равенство P(K Î V_КР / Н₀) = a, т.е. вероятность попадания К в V_КР при верной гипотезе Н₀ равна заданному числу a.

При малом значении a вступает в силу следующий принцип: маловероятное событие в единичном испытании практически невозможно. Практическим подтверждением справедливости этого принципа является игра «Русская рулетка».

Значит, если в результате эксперимента событие (K Î V_КР) не выполнится, то гипотезу следует принять. В противном случае ее надо отвергнуть, т.к. при верной гипотезе данное событие практически невозможно, а если наступило – то гипотеза не верна.

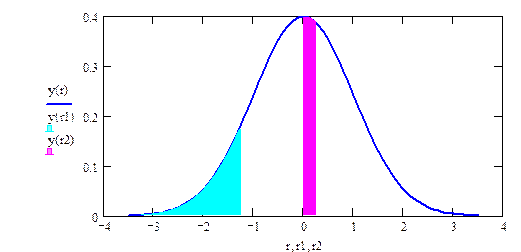
Построение оптимальной критической области. При сформулированном подходе V_КР не может быть определена однозначно, т.к. при любом законе распределения существует бесконечно много областей, вероятность попадания в которые равна заданному числу (см. рис. 2.1). Следовательно, метод нуждается в доработке. Для этого введем понятия ошибок I и II рода.

Def. Ошибка I рода состоит в отклонении верной гипотезы. Ошибка II рода состоит в принятии неверной гипотезы.

Чтобы понять разницу между этими понятиями – обратимся к примеру.

Пример 2.2. Система ПВО засекла летящий самолет. Гипотеза Н₀ – самолет вражеский. В данном примере ошибка I рода состоит в том, что при верной гипотезе она была отвергнута, и вражеский самолет пропустили на свою территорию. Ошибка II рода – гипотеза была неверна, но её приняли, в результате чего был сбит свой самолет. Приведенный пример, в частности демонстрирует, что, как правило, цена ошибок I и II рода различна.

В принятых обозначениях P_I = P(KÎV_КР / Н₀) = a – вероятность ошибки I рода; P_II = P( KÎ(V \V_КР) / 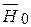) = b – вероятность ошибки II рода.

Принцип оптимального выбора V_КР состоит в следующем: при заданном уровне P_I = a  вероятность ошибки II рода должна быть минимальна (b ® min или 1– b® mах). Чтобы можно было оценить величину b, наряду с основной гипотезой Н₀ выдвигают конкурирующую гипотезу Н₁ = 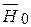, отвергающую основную.

Вернёмся к примеру 2.1. При основной гипотезе Н₀: m_x = 10 л выдвинем конкурирующую, например Н₁ : m_x = 9 л.  В качестве статистического критерия примем 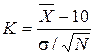.  При нормальном распределении СВ Х с параметрами      m_x = 10, D[X] = s² , т.е. при верной гипотезе Н₀, выбранный критерий К распределен нормально с параметрами m_К = 0, D[K] = 1. Если же предположить, что верна гипотеза Н₁, то случайная величина К имеет тоже нормальное распределение, но с параметрами D[K]=1,

m_К = 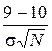 =  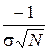= –2,5.                             (2.1)

Обозначим V_КР = [s, t ]. При заданном значении s величина t определяется из уравнения  

 P(KÎ[s, t ]) = a = U(t) – U(s),                               (2.2)

где  U(х) 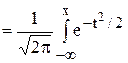– функция Лапласа (функция нормального распределения или интеграл вероятности). Отсюда

t = U^(–1)[a + U(s)].

Иными словами, t является (a + U(s))- квантилем нормального распределения. В  MathCad эта формула вычисления t имеет вид:

t:= qnorm(a + pnorm(s, 0, 1), 0, 1).                        (2.3)

Вероятность ошибки II рода равна

b = P( (KÏ V_КР ) / H₁ ) = P[KÎ( (–¥, s) 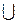 (t, +¥) )]= P[KÎ(–¥, s)] + P[KÎ(t, +¥)].

С учётом (2.1) значение b в MathCad   вычисляется с помощью формулы

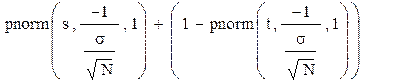            (2.4)

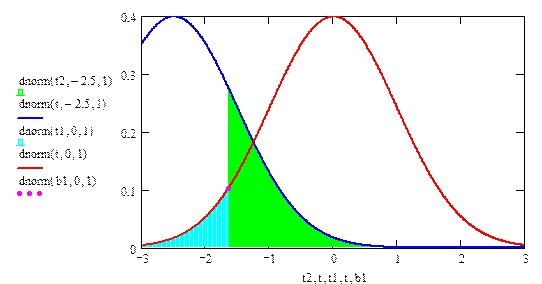
Теперь для нахождения оптимальной критической области надо определить значение s, при котором соблюдается условие (2.2) (т.е. (2.3)), а выражение (2.4) минимально. Несложно вычислить, что при a = 0.05 получим s^opt = –¥,  t^opt = – 1.64485, т.е. V_КР = [–¥, –1.645]. Такая область называется  левосторонней. При такой критической области b = 0.1962. На рис. 2.2 графически показаны значения a и b, найденные по формулам (2.2) и (2.4) при оптимальных границах критической области..

Def. Гипотеза вида q = b, где b – фиксированное число, называется простой.

При ней однозначно определяется распределение анализируемой СВ Х.

Def. Гипотеза вида q Î В, где В – фиксированное множество, называется сложной.

Например, гипотезы q < a, q ¹ a (а – число) – сложные.

Пусть в примере 2.1 основная гипотеза имеет вид m_x = 10. Тогда при любой простой конкурирующей гипотезе m_x = b, где b < 10, критическая область будет иметь ту же структуру, что и при конкурирующей гипотезе m_x = 9. То есть будем иметь левостороннюю критическую область V_КР = (– ¥, t_a), где квантиль t_a определяется из условия Р(К £ t_a) = a. Следовательно, при сложной конкурирующей гипотезе m_x < 10 критическая область будет такой же, см. рис. 2.3.

Соответственно, при сложной конкурирующей гипотезе m_x >10 оптимальная критическая область будет правосторонней, т.е. V_КР = ( t_{1– a}, + ¥), где t_{1– a} определяется из условия Р(К < t_{1– a}) = 1 – a или Р(К ³ t_{1– a}) = a. При a = 0.05 будет t_{1– a} = 1.64485.

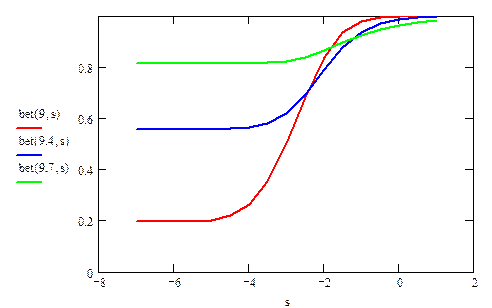
Рис 2.3. Значение b(s) при различных простых конкурирующих гипотезах:                – m_Х = 9;                – m_Х = 9.4;                  – m_Х = 9.7. Минимум везде достигается при s = – ¥

Наконец, при сложной конкурирующей гипотезе m_x ¹ 10 оптимальная критическая область будет двухсторонней, т.е.

V_КР = (– ¥, t_a/2)  ( t_{1– a/2}, + ¥),

где t_{1– a/2} определяется из условия Р( К ³ t_{1– a/2}) = a/2 и Р( К < t_a/2) = a/2. При a = 0.05 будет t_{1– a/2} = 1.95997 а t_a/2 = –1.95997.