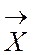Напомним, что эмпирические модели получаются в результате математической обработки данных экспериментов.

Статистическое моделирование – процесс построения эмпирической модели объекта, который имеет следующие особенности.

1) Любой объект моделирования представляется в виде «черного ящика», т. е. системы, в которой исследователю известны только водные данные и выходные, а внутренняя структура объекта неизвестна.

2) Применяется статистический подход – т. е. происходит наблюдение и обработка большого числа экспериментов (в каждом эксперименте происходят ошибки, но при большом количестве экспериментов можно уловить важные закономерности, исследуя какую-нибудь усредненную величину)

			ζ

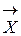 – набор (вектор) контролируемых входных параметров;

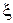 – неконтролируемые входные параметры (случайные помехи);

Y– выходной параметр.

3) Любые сделанные выводы и их последствия имеют вероятностный характер. Иными словами, после проведения исследований объекта средствами статистического моделирования, должны делаться какие-выводы о свойствах объекта. Их особенность состоит в том, что они в принципе не могут быть верными со 100%-й гарантией, всегда существует малая вероятность их ошибочности.

Тема 1.  Основные понятия теории вероятностей и математической

Статистики

Случайные векторы и их характеристики

Основные понятия.

Def . Случайным вектором 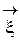 называется вектор, координатами которого являются случайные величины: .

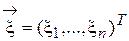Набор (x₁,…, x_n) называют также системой случайных величин. Как и обычные (скалярные) случайные величины, случайные векторы бывают непрерывными и дискретными.

Исчерпывающей вероятностной характеристикой случайного вектора является его функция распределения (функция совместного распределения системы случайных величин).

Def . Функция распределения F(x₁,…, x_n) случайного вектора 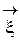 равна вероятности следующего сложного события: {( x₁< x₁) Ù … Ù ( x_n< x_n)}.

Def. Плотностью совместного распределения системы случайных величин (плотностью распределения случайного вектора) называется функция

.

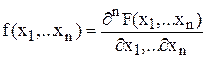Имеет место также следующая формула

.

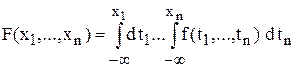Пусть D Ì E ⁿ – некоторая область n-мерного пространства. Тогда вероятность попадания случайного вектора в область D равна следующему n-кратному интегралу:

.

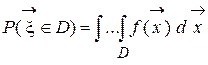Например, для одномерной случайной величины Р(xÎ[a, b]) = 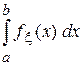, а при а = – ¥ будет Р(xÎ[– ¥, b]) = Р(x < b) = F_x (b).