Рассмотрим важнейшие свойства тех законов распределения вероятностей, которые чаще всего используются в математической статистике для проверки гипотез и в других приложениях.

2.2.1. Многомерное нормальное распределение. Плотность обычного нормального распределения имеет вид

.

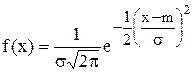Пусть Х – случайный вектор, компоненты которого распределены нормально, m – вектор математического ожидания Х, D – ковариационная матрица (будем обозначать это ХÎN(m, D)). Тогда плотность распределения вектора Х определяется выражением

.

Теорема 2.1 (свойство воспроизводимости нормального распределения). Пусть ХÎN(m, D). Тогда вектор Y = AX, где АА^Т – невырожденная матрица, распределен также нормально, YÎN(Аm, ADA^Т).

В частности, при Y = 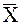 будет A = 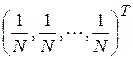, а следовательно, при нормальном распределении СВ Х оценка  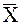будет также нормально распределена.

2.2.2. c ²-распределение Пирсона (хи-квадрат).

Def. Пусть имеем случайный вектор ХÎN(0, I_n), где I_n – единичная матрица порядка n. Тогда скалярная СВ x = Х^ТХ имеет распределение Пирсона с n степенями свободы (n – параметр распределения). Будем обозначать это xÎc²(n)

Приведем основные свойства распределения Пирсона.

Теорема 2.2 (о критерии Пирсона). Пусть Х₁,…, Х_N – выборка некоторой скалярной СВ Х. Разобьем область значений элементов выборки на m частей  (m ³ 2) произвольной ширины, обозначив их D₁,…, D_m. Пусть F(x) – некоторая функция распределения. Введем следующую статистику (статистический критерий Пирсона)

,

где n_i – число элементов выборки, попавших в D_i; p_i – вероятность попадания в D_i СВ, распределенной по закону F(x). Тогда если СВ Х имеет функцию распределения F(x), то при N ® ¥ распределение СВ 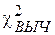стремится к распределению Пирсона с n = m – k – 1 степенями свободы, где k – число параметров функции F(x), оценки которых найдены по данной выборке.

Резюме. Данная теорема описывает основное применение распределения Пирсона. Главное достоинство критерия c² в том, что он применим к любой функции распределения. Если F(x) – предполагаемый закон распределения, то проверка этого факта сводится к проверке соответствующей статистической гипотезы с правосторонней критической областью (t_1–a, +¥). При 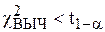 принимается гипотеза о том, что F(x) действительно является функцией распределения СВ Х. В противном случае гипотеза отвергается.

Замечание. Поскольку, согласно теореме 2.2, распределение Пирсона для статистики 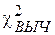 имеет место лишь в пределе при N ® ¥, то ограничительным условием применения данного критерия является достаточно большой объем выборки. На практике он используется, когда для всех n_i справедливо неравенство n_i ³ 5. Исходя из этого соображения, определяется число m интервалов. Если данное неравенство не выполняется, то соседние интервалы необходимо объединить, так, чтобы условие выполнялось. Напоминаем, что интервалы могут иметь произвольную и не обязательно одинаковую ширину.

Теорема 2.3 (о распределении оценки s²). Пусть ХÎN(m, s²I_N). Тогда

1) (N – 1) s² / s² Î c²(N – 1).

2) СВ s² и независимы.

2.2.3. t-распределение Стьюдента и F-распределение Фишера

Def. Пусть xÎN(0, 1) и w_nÎc²(n) – независимые СВ. Тогда СВ

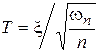
имеет t-распределение Стьюдента с n степенями свободы.

Def. Пусть w_nÎc²(n) и h_mÎc²(m) – независимые СВ. Тогда СВ 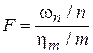 имеет F-распределение Фишера с n и m степенями свободы.

Рассмотрим два приложения теоремы 2.3 и t- и F-распределений к проверке статистических гипотез.

Приложение 1. Пусть имеем выборку Х₁, …, Х_N, Х_j Î N(a, s²). Тогда случайный вектор (Х₁,…, Х_N)^Т удовлетворяет теореме 2.3. Следовательно СВ 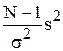 имеет распределение c²(N – 1) и не зависит от 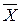. Но 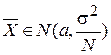 по свойству воспроизводимости. Значит  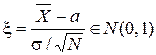и не зависит от s². Поэтому СВ  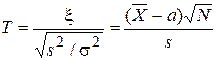имеет t-распределение Стьюдента с    N – 1 степенями свободы.

Это означает, что если СВ Х распределена нормально, то статистика Т может быть использована в качестве статистического критерия проверки гипотезы вида Н₀: M[X] = a, где а – заданное число, причем знание s не требуется.

Критические области:

- Н₁: M[X] < a – левосторонняя (– ¥, t_a);

- Н₁: M[X] > a – правосторонняя (t_{1– a}, +¥);

- Н₁: M[X] ¹ a – двухсторонняя (– ¥, t_a/2) 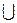( t_{1– a/2},  +¥).

Пример 2.3. Масса Х пачки печенья должна быть равна 200 г. Выборочное взвешивание N = 25 пачек дало следующие оценки 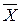= 196.64 г, s² = 36 г². Нет ли на фабрике систематического недовеса?

Решение. Выдвигаем гипотезу Н₀: M[X] = 200 при Н₁: M[X] < 200 (Н₁ означает недовес). 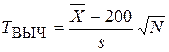= –2.8. При a = 0.05 получим t_a= –1.711. Значит Т_ВЫЧ ÎV_КР и основная гипотеза не верна, на фабрике имеет место недовес.

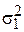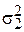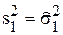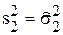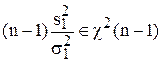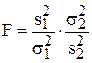Приложение 2. Пусть имеем две выборки: Х₁, …, Х_n; Х_j Î N(a₁, ) и Y₁, …, Y_m; Y_i Î N(a₂, ). Пусть , . Согласно теореме 2.3 , а . Следовательно СВ  имеет F-распределение с  n – 1 и m – 1 степенями свободы. В частности, при  такое же распределение имеет СВ .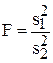

Таким образом СВ F можно использовать в качестве статистического критерия проверки гипотезы 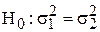. Если s₁ > s₂, то альтернативная гипотеза имеет вид  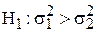с правосторонней критической областью (t_{1– a}, +¥).        

Тема 3.  Регрессионный анализ: исследование свойств регрессии

Регрессионный анализ – раздел математической статистики, посвященный методам синтеза и анализа наиболее распространенного класса статистических моделей – уравнений регрессии (см. п. 1.4)

Основное допущение, лежащее в основе метода: экспериментальные ошибки (компоненты вектора e) независимы и распределены нормально. Причем данный факт не надо принимать на веру, его можно проверить с помощью критерия Пирсона.

Свойства МНК -оценок. Рассмотрим некоторые свойства МНК-оценок, вытекающие из предположения о нормальности компоненты вектора e.

Теорема 3.1 (о нормальности МНК-оценок). Если выполнены условия теоремы Гаусса-Маркова и eÎN(0, s²I), то

1) МНК-оценки распределены нормально: 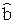 Î N (b, s²(Ф^T Ф)^–1).

2) Статистика 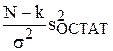 имеет распределение c² с числом степеней свободы n = N – k.

3) Случайные величины 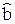 и  независимы.

Доказательство. 1) Следует из теоремы 2.1– свойства воспроизводимости нормального распределения.

Теорема 3.1 позволяет разработать методы анализа построенного уравнения регрессии с использованием аппарата проверки статистических гипотез.