Для простейшего анализа свойств уравнения (1.3) необходимо выполнение условий теоремы Гаусса-Маркова: 

- M[e] = 0, т.е. систематические ошибки в эксперименте отсутствуют;

- D[e] = s² I , т.е. ошибки во всех экспериментах имеют одинаковую дисперсию и независимы.

Коэффициент детерминации. Обозначим 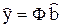 – статистическая оценка вектора M[у], полученная с помощью МНК. Обозначим 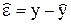– оценка вектора случайных ошибок e. Напомним: e = у – M[y]. Из уравнения (1.4) имеем

Ф^Т (у – Ф 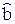) = Ф^Т  = 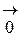.                                   (1.6)

Отсюда получаем

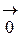а) Для любого вектора z выполняется: z^Т Ф  = 0, т.к. умножение на любого вектора даст скалярный 0.

б) Предположим, что модель (1.3) имеет свободный член, т.е. f₁(x) º1. Тогда 1-й столбец матрицы Ф полностью состоит из единиц. Следовательно, для 1-го столбца уравнение (1.6) примет вид å = 0.

Обозначим åу_j и оценим величину Q_ОБЩ = å(у_j – 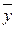)² – разброс компонент вектора у. Имеем

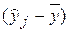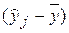Q_ОБЩ = å[(у_j – )+ ]² =å (у_j – )²+ 2å(у_j – ) + å ².

Найдем А = å(у_j – ) 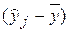= å 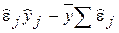. Вторая сумма равна 0 по свойству б). Первую сумму представим в виде å 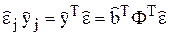. Полагая в выражении а) z = 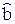, получим  = 0. Следовательно, А = 0. Отсюда 

Q_ОБЩ = å(у_j – ) ² + å 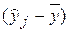 ² = Q_ОСТАТ + Q_РЕГР,     (1.7)

где Q_ОСТАТ – остаточная сумма квадратов (обусловлена случайными отклонениями экспериментальных данных от расчетных);

  Q_РЕГР – сумма квадратов, обусловленная регрессией (отклонение расчетных данных от среднего).

Геометрический смысл этих сумм представлен на рис.1.3 а), б), в).

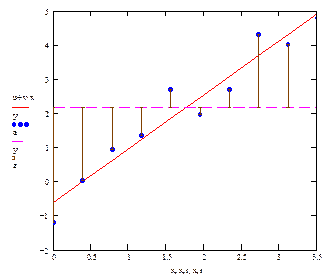
Рис. 1.3 а) Q_ОБЩ  – сумма квадратов длин вертикальных отрезков – отклонений y _i (точки) от 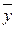(пунктир).

Введем величину

 –

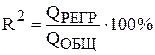коэффициент детерминации, показывающий процентную долю общего разброса компонент вектора у, объясняемую регрессией (влиянием входных контролируемых параметров). С его помощью можно оценивать качество построенной модели: чем больше R², тем точнее считается уравнение регрессии. Как показывает опыт, достаточно хороший результат – R² ³ 90%.

Рис. 1.3 б) Q_ОСТАТ  – сумма квадратов длин вертикальных отрезков– отклонений y _i (точки) от 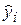(сплошная линия).

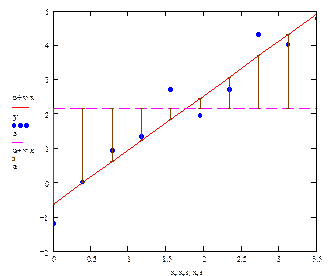
Рис. 1.3 в) Q_РЕГР  – сумма квадратов длин вертикальных отрезков –отклонений 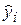(сплошная линия) от 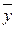(пунктир).

Остаточная дисперсия

Def. Остаточной дисперсией уравнения регрессии называется величина

=

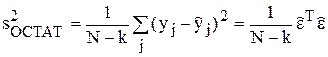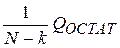
равная среднему квадрату отклонения экспериментальных данных от расчетных (k – число коэффициентов модели (1.3)).

Теорема 1.6 (о несмещенногсти остаточной дисперсии). Если выполнены условия теоремы Гаусса-Маркова, то остаточная дисперсия является несмещенной оценкой параметра s².

Следствие. 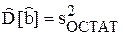(Ф^TФ)^–1 – несмещенная оценка.

Значение остаточной дисперсии позволяет оценить точность построенного уравнения. Из нескольких альтернативных вариантов модели при прочих равных условиях предпочтение следует отдавать уравнению, имеющему наименьшую остаточную дисперсию.

МНК-прогноз. Пусть х – фиксированный вектор входных параметров. С помощью модели (х) = 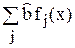 можно предсказать каким в среднем будет значение выходного параметра у при входе х, т.е. (х) – прогноз выхода при заданном входе. Так как МНК-оценки – случайные величины, то (х) – тоже случайная величина, как и всякая статистическая оценка. Её дисперсия характеризует среднюю точность прогноза. Найдем D[ (х)] и ее оценку.

Обозначим f(x) = [f₁(x),…, f_k(x)]^Т – вектор базисных функций. Тогда 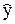(х) = f^T(x) 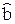. Воспользуемся теоремой 1.2 о линейно зависимых векторах  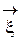=  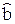и 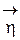= (х), положив в ней А = f^T(x).

D[ (х)] = f^T(x) D[ 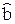] f(x) = s² f^T(x) (Ф^T Ф)^–1f(x).      (1.8)

Значит, согласно следствию из теоремы 3.1 об остаточной дисперсии

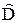[ (х)] = 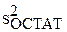f^T(x) (Ф^T Ф)^–1f(x).

Теорема 3.2 (об МНК-прогнозе). Если выполнены условия теоремы Гаусса-Маркова, то прогноз (х) является несмещённой эффективной оценкой в классе линейных по у несмещенных оценок.

Доказательство. Линейность прогноза следует из линейности .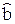

Докажем несмещенность. По теореме 1.2 имеем M[ (х)] = f^T(x)M[ 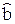] = = f^T(x) b = M[y(x)] – несмещенная оценка.

Тема 2.   Проверка статистических гипотез