Определение. Уравнение  второй степени относительно x, y, z вида
второй степени относительно x, y, z вида 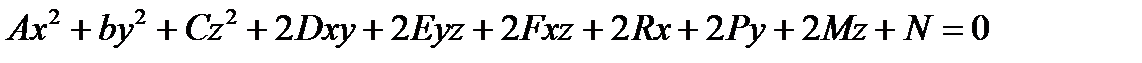 , где А, В, С одновременно не равны нулю, называется общим уравнением поверхности второго порядка (квадриком).
, где А, В, С одновременно не равны нулю, называется общим уравнением поверхности второго порядка (квадриком).
Этому уравнению не всегда соответствует на плоскости множество точек. Если геометрический образ не существует, то есть нет точек, удовлетворяющих уравнению, то говорят, что уравнение определяет мнимую поверхность.
Из общего уравнения получаются многочисленные уравнения поверхностей – канонические уравнения. Приведение общего уравнения к каноническому виду осуществляется путем образования полных квадратов по отношению к переменным х, у, z и параллельному переносу начала координат в точку (х0, у0, z0).
Пример. Вывести каноническое уравнение сферы с центром в точке М0(х0, у0, z0) и радиусом R.
Вывод.
Определение. Сфера – геометрическое место точек, расстояние от которых до данной точки М0(х0, у0, z0) – центра есть величина постоянная и равная R.
Рассмотрим текущую точку сферы М(х, у, z). Тогда 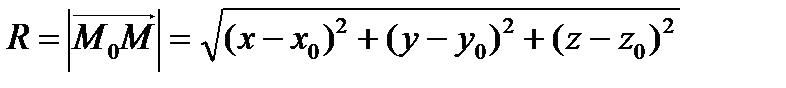 . Отсюда
. Отсюда  – каноническое уравнение сферы с центром в точке М0(х0, у0, z0) и радиусом R.
– каноническое уравнение сферы с центром в точке М0(х0, у0, z0) и радиусом R.
Канонические уравнения основных поверхностей второго порядка
1. 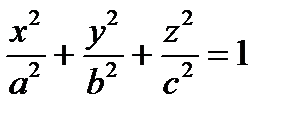 – уравнение эллипсоида
– уравнение эллипсоида
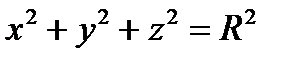 – уравнение сферы
– уравнение сферы
2. 1) 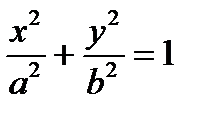 ,
, 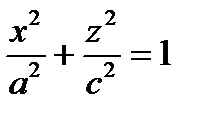 ,
, 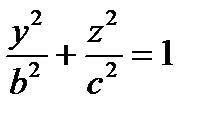 – эллиптические цилиндры
– эллиптические цилиндры
2)  ,
, 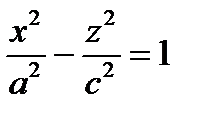 ,
, 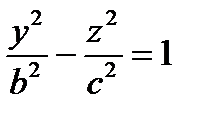 ,
,  ,
, 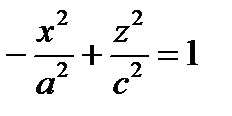 ,
, 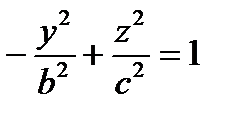 – гиперболические цилиндры
– гиперболические цилиндры
3) 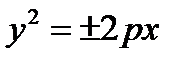 ,
,  , g)
, g) 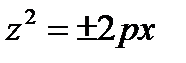 ,
, 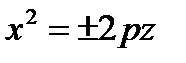 ,
, 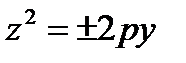 ,
,  – параболические цилиндры
– параболические цилиндры
3.  ,
, 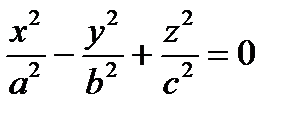 ,
,  – уравнения конуса.
– уравнения конуса.
4. 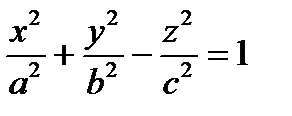 ,
, 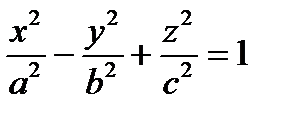 ,
, 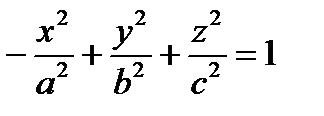 – уравнения однополостного гиперболоида.
– уравнения однополостного гиперболоида.
5.  ,
, 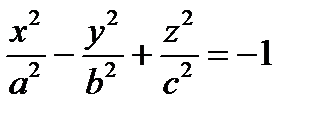 ,
, 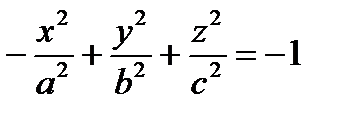 – уравнения двуполостного гиперболоида.
– уравнения двуполостного гиперболоида.
6. 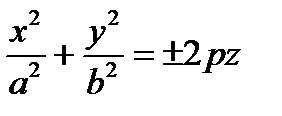 ,
, 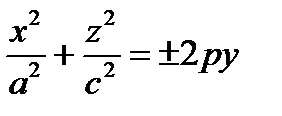 ,
, 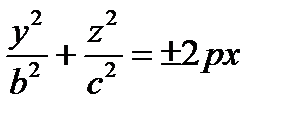 – уравнения эллиптического параболоида.
– уравнения эллиптического параболоида.
7. 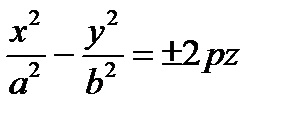 ,
, 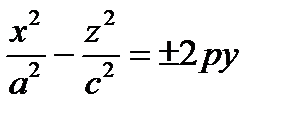 ,
, 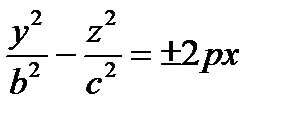 – уравнения гиперболического параболоида.
– уравнения гиперболического параболоида.
Цилиндрические поверхности
Пусть в общем уравнении поверхности отсутствует одна координата, например z, т.е. уравнение имеет вид: 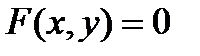 . Тогда вместе с точкой М0(х0, у0, z0), лежащей на поверхности, на ней будет лежать и прямая, параллельная оси (О z) и проходящая через точку М1(х0, у0, 0).
. Тогда вместе с точкой М0(х0, у0, z0), лежащей на поверхности, на ней будет лежать и прямая, параллельная оси (О z) и проходящая через точку М1(х0, у0, 0).
Определение. Уравнение 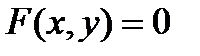 называется уравнением направляющей, которой является кривая второго порядка. Прямые, проходящие через точки кривой, параллельно оси (О z), называются образующими.
называется уравнением направляющей, которой является кривая второго порядка. Прямые, проходящие через точки кривой, параллельно оси (О z), называются образующими.
Определение. Цилиндрической поверхностью или цилиндром называется поверхность, в общем уравнении которой отсутствует одна координата: 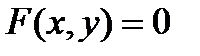 или
или 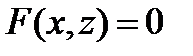 или
или 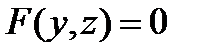 .
.
| х |
| у |
| z |
| а |
| b |
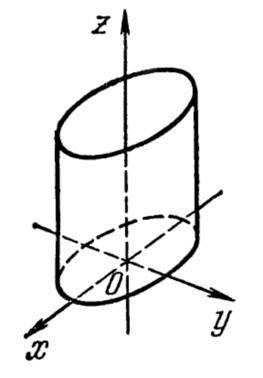
1). Эллиптические цилиндры.
а) 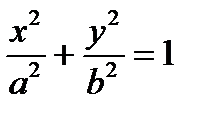
В уравнении поверхности отсутствует координата z, следовательно,
образующие параллельны оси (О z), направляющая – эллипс
в плоскости (Оху) с центром в точке О.
b) 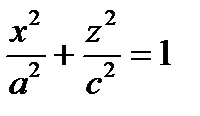
В уравнении поверхности отсутствует координата у, следовательно, образующие
параллельны оси (Оу), направляющая – эллипс в плоскости (Ох z) с центром в точке О.
с) 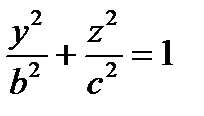
В уравнении поверхности отсутствует координата х, следовательно, образующие
параллельны оси (Ох), направляющая – эллипс в плоскости (Оу z) с центром в точке О.
| х |
| у |
| z |
| а |
 .
.
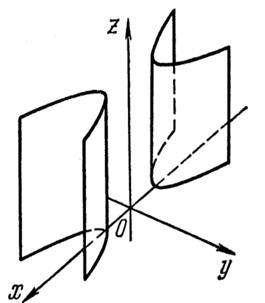
2). Гиперболические цилиндры.
а) 
В уравнении поверхности отсутствует координата z, следовательно, образующие параллельны оси (О z), направляющая – гипербола в плоскости (Оху) с центром в точке О.
b) 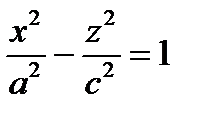
В уравнении поверхности отсутствует координата у, следовательно, образующие
параллельны оси (Оу), направляющая – гипербола в плоскости (Ох z) с центром в точке О.
с) 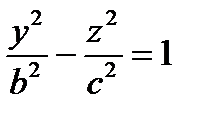
В уравнении поверхности отсутствует координата х, следовательно, образующие параллельны оси (Ох), направляющая – гипербола в плоскости (Оу z) с центром в точке О.
d)  , e)
, e) 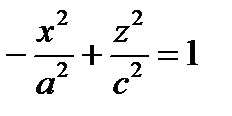 , g)
, g) 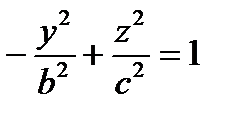
Замечание. Уравнение гиперболического цилиндра, вытянутого вдоль оси (О z) с направляющей с центром в точке М1(х0, у0, 0) имеет вид: 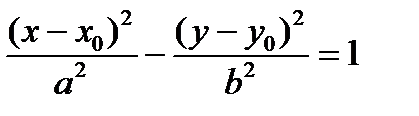 .
.
| х |
| у |
| z |
а ) 
В уравнении поверхности отсутствует координата z,
следовательно, образующие параллельны оси (О z),
направляющая – парабола в плоскости (Оху) с вершиной в точке О.
b) 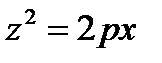
В уравнении поверхности отсутствует координата у,
следовательно, образующие параллельны оси (Оу),
направляющая – парабола в плоскости (Ох z) с вершиной в точке О.
с) 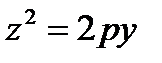
В уравнении поверхности отсутствует координата х, следовательно, образующие
параллельны оси (Ох), направляющая – парабола в плоскости (Оу z) с вершиной в точке О.
d) 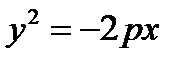 , e)
, e)  , g)
, g)  , f)
, f) 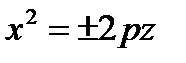 , h)
, h) 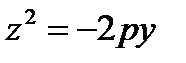 , k)
, k)  .
.
Замечание. Уравнение параболического цилиндра, вытянутого вдоль оси (О z) с направляющей – параболой, симметричной оси (Ох) и с вершиной в точке М1(х0, у0, 0) имеет вид: 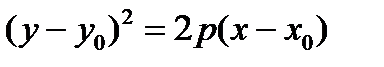 .
.

Конические поверхности
Определение. Конической поверхностью или конусом называется поверхность, образованная точками прямых, проходящих через данную точку – вершину и пересекающих данную прямую направляющую.
Канонические уравнения конуса: 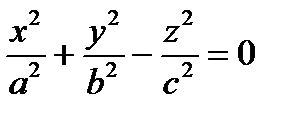 ,
, 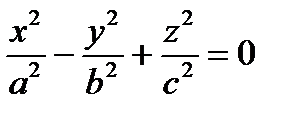 ,
, 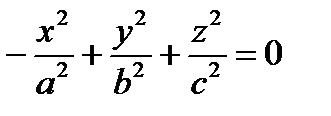 .
.
Перед какой переменной стоит знак «–», вдоль той оси вытянут конус.
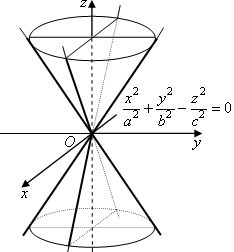
Исследуем форму конуса, заданного уравнением 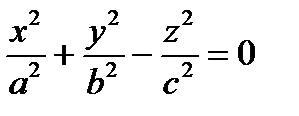 методом сечений.
методом сечений.
Метод сечений заключается в том, что поверхность пересекают плоскостями, параллельными координатным плоскостям, и изучают линии, получающиеся при пересечении.
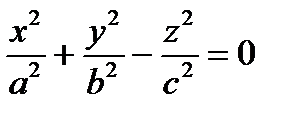 .
.
1)  , удобнее брать h = 0, т.е.
, удобнее брать h = 0, т.е.  две пересекающиеся прямые в точке О в плоскости (О yz).
две пересекающиеся прямые в точке О в плоскости (О yz).
2) 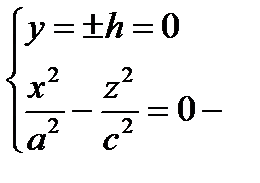 две пересекающиеся прямые в точке О в плоскости (Oxz)
две пересекающиеся прямые в точке О в плоскости (Oxz)
3) 
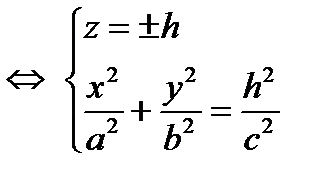
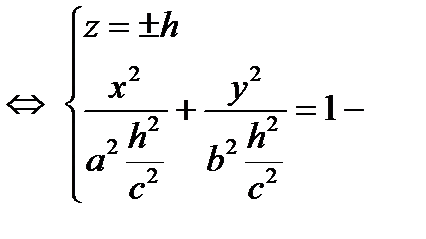 уравнение эллипса в плоскостях, параллельных плоскости (Оху)
уравнение эллипса в плоскостях, параллельных плоскости (Оху)
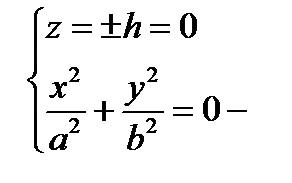 точка О.
точка О.
| х |
| у |
| z |
| О |
| h |
| - h |
Построение.
Замечание. Уравнение конуса, вытянутого вдоль оси (О z) с вершиной в точке М0(х0, у0, z0) имеет вид:  .
.
Эллипсоид.
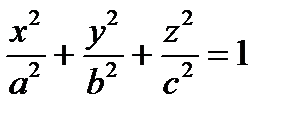 – каноническое уравнение эллипсоида.
– каноническое уравнение эллипсоида.
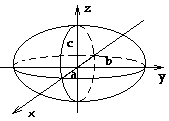
Исследуем его форму методом сечений.
1)  , удобнее брать h = 0, т.е.
, удобнее брать h = 0, т.е. 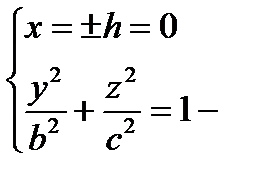 эллипс в плоскости (Oyz)
эллипс в плоскости (Oyz)
2) 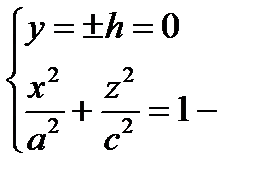 эллипс в плоскости (Oх z)
эллипс в плоскости (Oх z)
3) 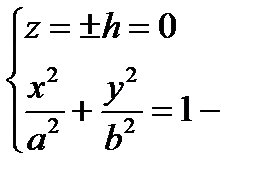 эллипс в плоскости (Oх y)
эллипс в плоскости (Oх y)
Замечание. Уравнение эллипсоида с центром в точке М0(х0, у0, z0) имеет вид:  .
.
Гиперболоиды
Однополостный гиперболоид
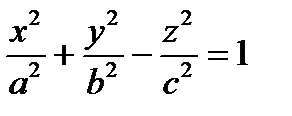 ,
, 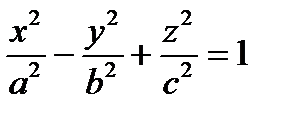 ,
, 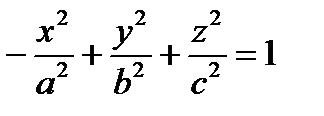 – канонические уравнения однополостного гиперболоида.
– канонические уравнения однополостного гиперболоида.
Перед какой переменной стоит знак «–», вдоль той оси вытянут гиперболоид.
Исследуем форму однополостного гиперболоида, заданного уравнением 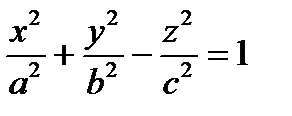 , методом сечений.
, методом сечений.
1) 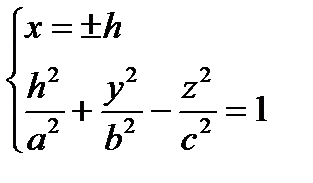 , удобнее брать h = 0, т.е.
, удобнее брать h = 0, т.е. 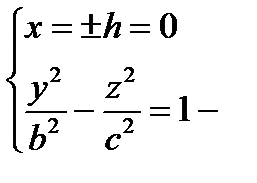 гипербола в плоскости (Oyz), ветви симметричны (О z)
гипербола в плоскости (Oyz), ветви симметричны (О z)
2) 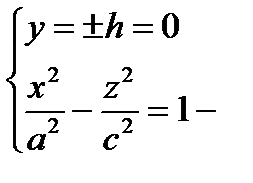 гипербола в плоскости (Oх z), ветви симметричны (О z)
гипербола в плоскости (Oх z), ветви симметричны (О z)
3) 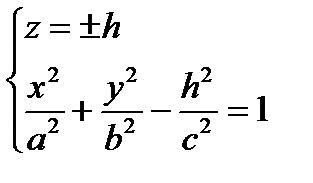
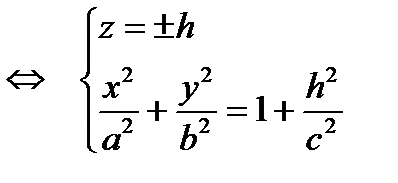
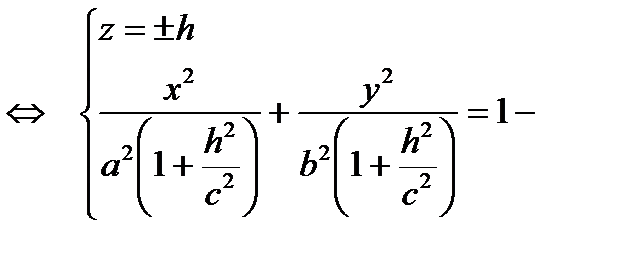 эллипсы, лежащие в плоскостях, параллельных плоскости (Оху)
эллипсы, лежащие в плоскостях, параллельных плоскости (Оху)
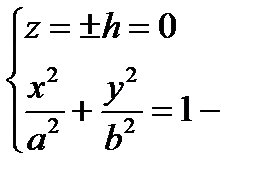 эллипс в плоскости (Oх y).
эллипс в плоскости (Oх y).
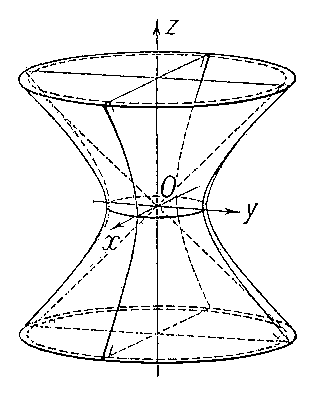
Замечание. Уравнение однополостного гиперболоида с центром в точке М0(х0, у0, z0), вытянутого вдоль оси (Oz), имеет вид: 
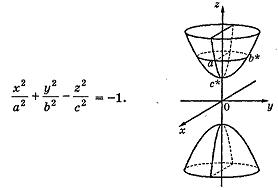
Двуполостный гиперболоид
 ,
, 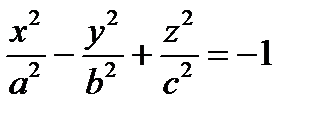 ,
, 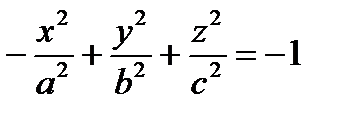 – канонические уравнения двуполостного гиперболоида.
– канонические уравнения двуполостного гиперболоида.
Перед какой переменной стоит знак «–», на той оси вытянут гиперболоид.
Исследуем форму двуполостного гиперболоида, заданного уравнением 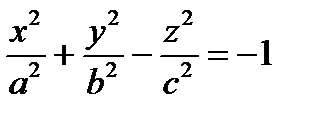 , методом сечений.
, методом сечений.
1) 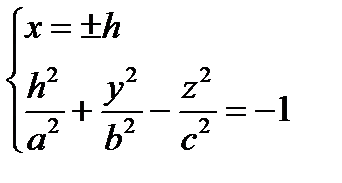 , удобнее брать h = 0, т.е.
, удобнее брать h = 0, т.е. 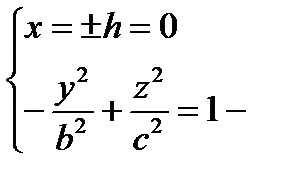 гипербола в плоскости (Oyz), ветви симметричны (Оу)
гипербола в плоскости (Oyz), ветви симметричны (Оу)
2) 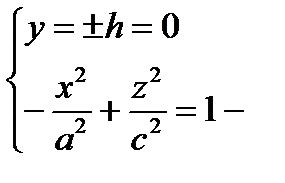 гипербола в плоскости (Oх z), ветви симметричны (Ох)
гипербола в плоскости (Oх z), ветви симметричны (Ох)
3) 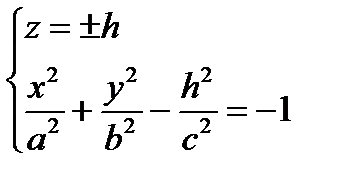
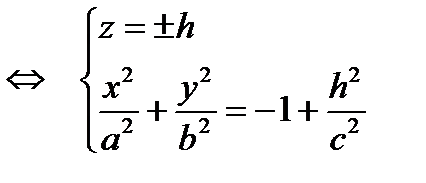
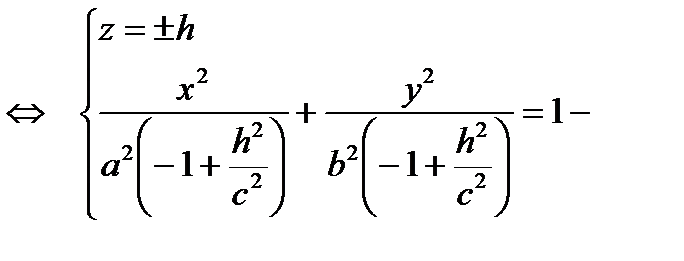 эллипсы, лежащие в плоскостях, параллельных плоскости (Оху)
эллипсы, лежащие в плоскостях, параллельных плоскости (Оху)
Очевидно, что должно выполняться неравенство: 
Значение z = 0 не может быть. 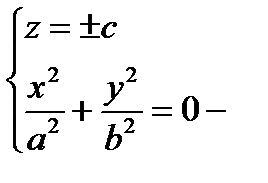 точки с координатами в (0, 0, ±с).
точки с координатами в (0, 0, ±с).
Замечание. Уравнение двуполостного гиперболоида с центром в точке М0(х0, у0, z0), расположенного вдоль оси (Oz), имеет вид: 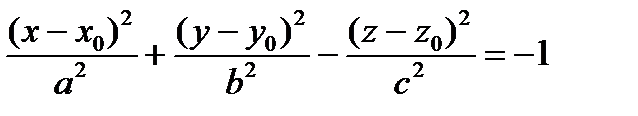 .
.
Параболоиды
Эллиптический параболоид
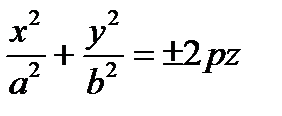 ,
, 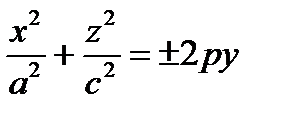 ,
,  – канонические уравнения эллиптического параболоида.
– канонические уравнения эллиптического параболоида.
Какая переменная стоит в первой степени – вдоль той оси вытянут параболоид, знак «+» или «–» показывает направление.
Исследуем форму эллиптического параболоида, заданного уравнением 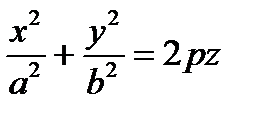 , методом сечений.
, методом сечений.
1)  , удобнее брать h = 0, т.е.
, удобнее брать h = 0, т.е. 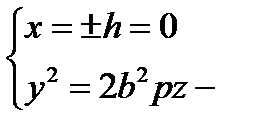 парабола с вершиной в точке О вдоль оси z в плоскости (Oyz) (ветви вверх)
парабола с вершиной в точке О вдоль оси z в плоскости (Oyz) (ветви вверх)
2) 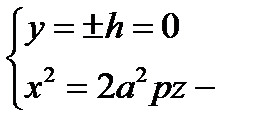 парабола с вершиной в точке О вдоль оси z в плоскости (Oх z) (ветви вверх)
парабола с вершиной в точке О вдоль оси z в плоскости (Oх z) (ветви вверх)
3) 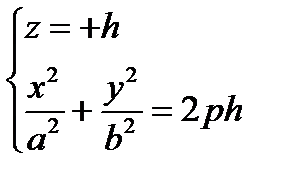
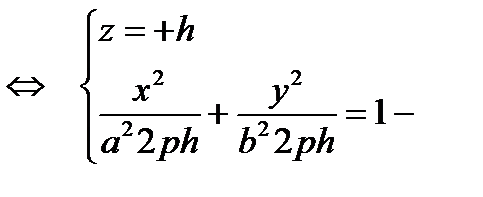 эллипсы, лежащие в плоскостях, параллельных плоскости (Oху)
эллипсы, лежащие в плоскостях, параллельных плоскости (Oху)
z = – h не может быть.
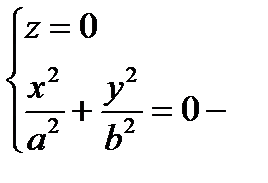 точка О.
точка О.

Замечание. Уравнение эллиптического параболоида с центром в точке М0(х0, у0, z0), расположенного вдоль оси (Oz), имеет вид:  .
.
Дата: 2019-02-24, просмотров: 417.