Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

Даны две плоскости:

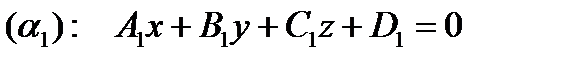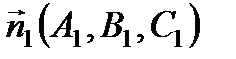
с нормальным вектором

 с нормальным вектором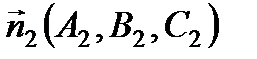

1. Пусть (α₁) 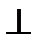 (α₂), тогда 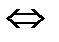 скалярное произведение этих векторов равно нулю, т.е. 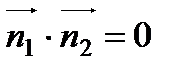, т.к. известны координаты векторов, то можем найти скалярное произведение как  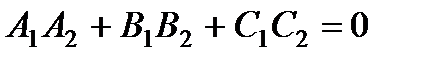– условие перпендикулярности двух плоскостей.

2. Пусть (α₁) 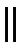 (α₂), тогда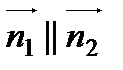 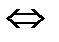 координаты пропорциональны, т.е.  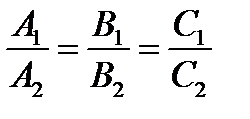– условие параллельности двух плоскостей.

3. Пусть (α₁) и (α₂) пересекаются.

Углом между плоскостями называется один из двух двугранных углов 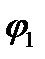 или 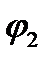, образованных этими плоскостями, причем ,  ,  +  = .

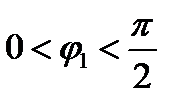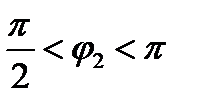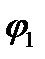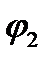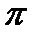Угол между плоскостями будет равен углу между нормалями плоскостей, следовательно, его можно найти с помощью скалярного произведения:

,

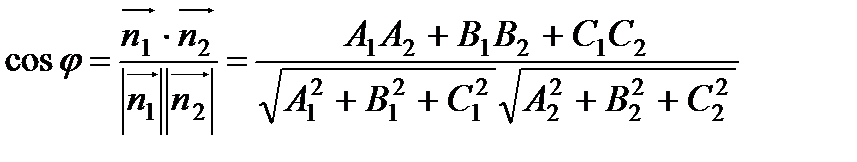если 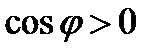, то получили угол 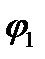, если 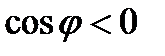, то получили угол .

 

М2

М1

2 способа построения плоскости

М3

Задача. Построить уравнение плоскости, проходящей через три заданные

точки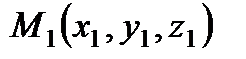

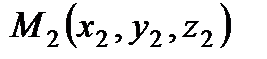
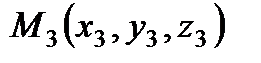
1 способ. Рассмотрим текущую точку плоскости 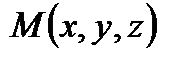. Построим три вектора (один неизвестный  и два известных), выходящие (желательно) из одной известной точки, например, :

, , .

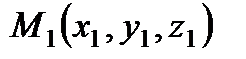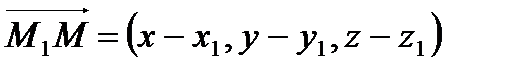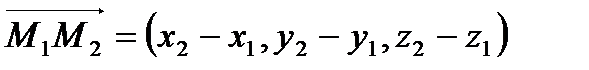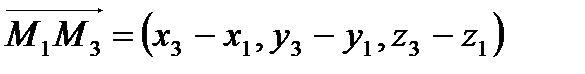Все три вектора лежат в одной плоскости. Три вектора компланарны только тогда, когда их смешанное произведение равно нулю:

М

М1

М3

М2

                                    . 

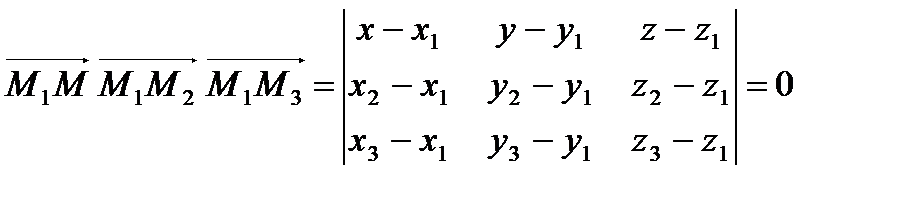Раскроем определитель и получим общее уравнение плоскости:

.

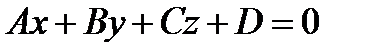М1

М3

М2

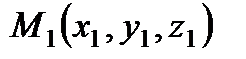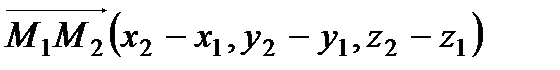2 способ.  Построим два вектора, выходящие (желательно) из одной точки, например,              : , . Нормальный вектор плоскости перпендикулярен плоскости, а значит перпендикулярен любым векторам, лежащим в этой плоскости, в частност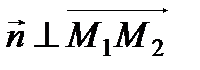и  и 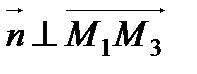, тогда для того, чтобы найти вектор 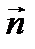, надо найти векторное произведение векторов  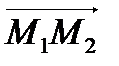и : .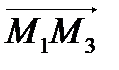

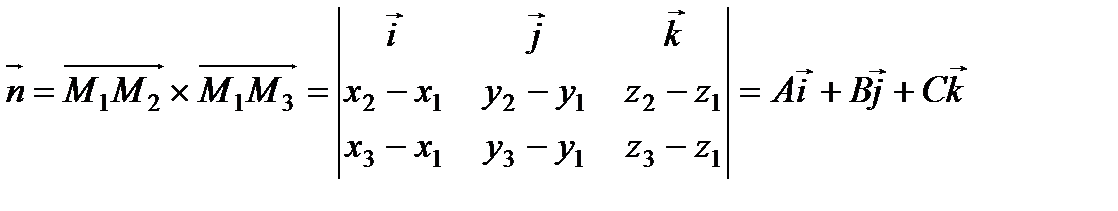Чтобы найти уравнение плоскости, надо, кроме нормального вектора знать координаты точки, лежащей в плоскости. В условии задачи их три. Можно взять любую. Возьмем точку 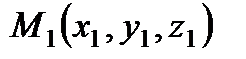. Тогда уравнение плоскости, проходящей через данную точку 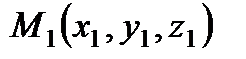, перпендикулярно заданному вектору  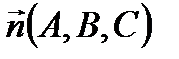имеет вид: 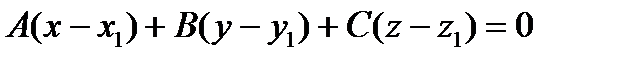. Раскроем скобки и получим общее уравнение плоскости: .

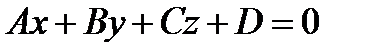П. 5. Прямая в пространстве

Рассмотрим в пространстве R³ прямую (а), проходящую через данную точку 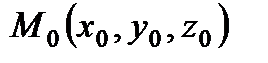, параллельно заданному вектору 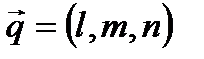. 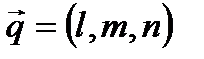– направляющий вектор прямой.       

М

М0

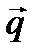
а

 

Вывод уравнения (а): Рассмотрим текущую точку прямой 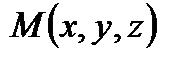 и рассмотрим вектор 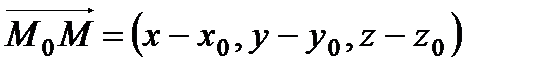, который будет лежать на прямой (а). Направляющий вектор прямой  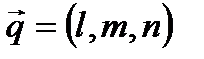параллелен прямой (а), следовательно, векторы  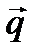и 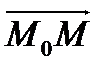 параллельны или коллинеарны. Условие коллинеарности двух векторов – пропорциональность их координат:

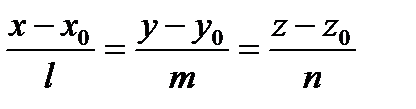                                        – канонические уравнения прямой.     (1)

 

Уравнение прямой, проходящей через две заданные точки 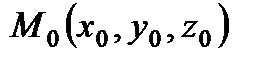 и

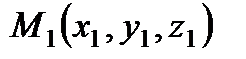
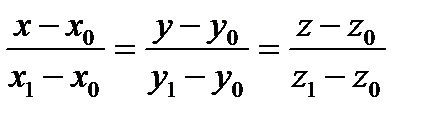                                                                                                               (2)

Вывод: Рассмотрим текущую точку прямой 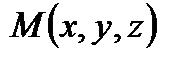 и рассмотрим векторы  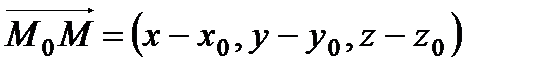и , которые будут параллельны. Условие коллинеарности двух векторов – пропорциональность их координат.

 

Приравняем уравнение (2) к параметру t: 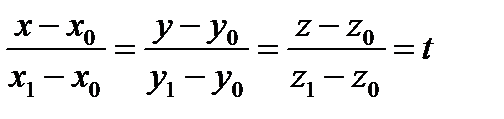, отсюда

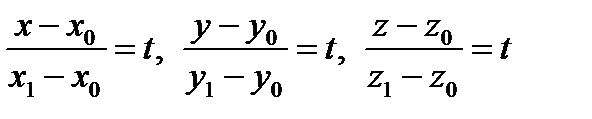или  – параметрическое уравнение прямой (3)

 

Множество точек пересечения двух различных плоскостей α₁ и α₂, имеющих общую точку:

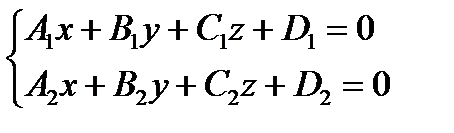                            – общее уравнение прямой                         (4).

Направляющий вектор данной прямой находится как 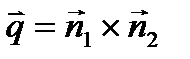, координаты точки             M₀(x₀, y₀ z₀), лежащей на прямой, удовлетворяют системе уравнений (4).