Однородная система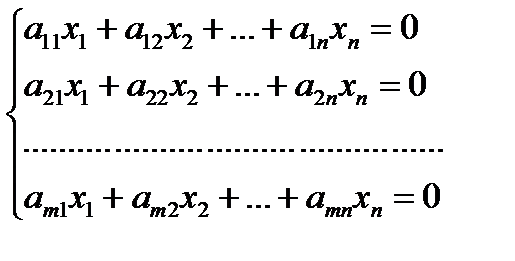 
всегда совместна, так как она всегда имеет нулевое решение 
= 
= …= 
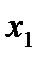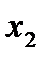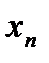= 0, оно называется тривиальным. Для нее справедливо, что 
.
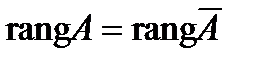Теорема Кронекера-Капелли для однородной системы: 1) если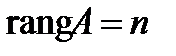 
, то система имеет единственное решение – нулевое, 2) если 
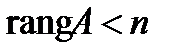, то система имеет бесконечное множество решений, среди которых есть и ненулевые.
Определение 23. Линейно независимая совокупность решений однородной системы называется фундаментальной системой решений, если каждое решение является линейной комбинацией остальных.
Идея метода Гаусса: матрица системы приводится к трапециевидной или к треугольной форме, затем все получившиеся базисные переменные выражаются через свободные переменные и находится фундаментальное решение системы.
Пример. Решить систему линейных уравнений: 
.
Решение. Запишем матрицу системы: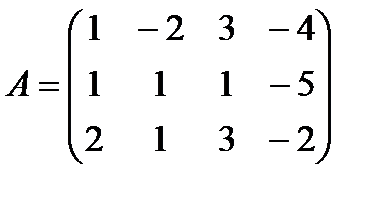 
,
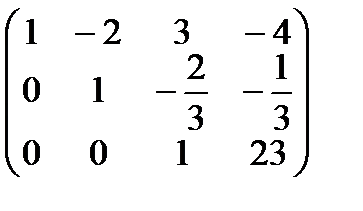отсюда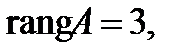 
т.к. три ненулевые строки. Количество неизвестных n = 4, т.е. 
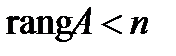, следовательно, по теореме Кронекера - Капелли система имеет бесконечное множество решений. Найдем его. Запишем полученную матрицу в виде системы уравнений:
.
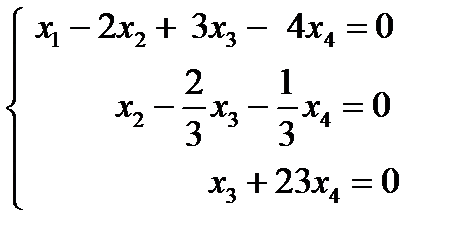Система имеет три базисные неизвестные: , ,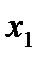 
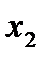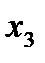и одну свободную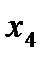 
.
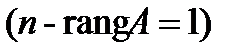Выразим базисные неизвестные через свободную переменную, начиная с последнего уравнения:
,
,
.
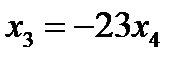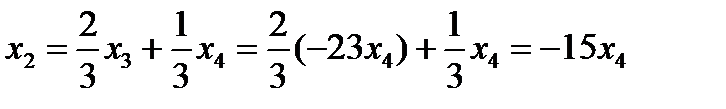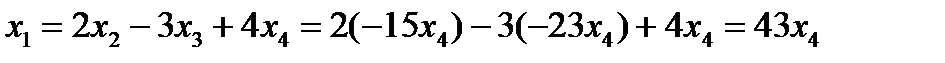Ответ: Фундаментальная система решений: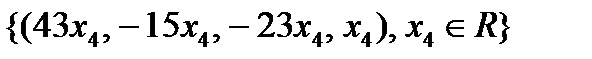 
.
Решение неоднородных систем методом Гаусса
Пример 1. Решить систему уравнений: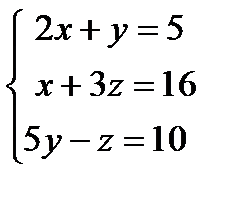 
.
Решение.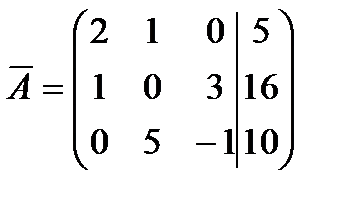 
.
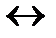
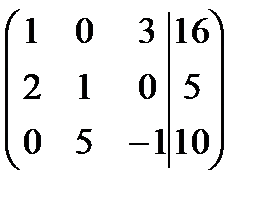
Проверим условия теоремы Кронекера-Капелли: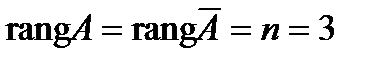 
, следовательно, система имеет единственное решение, найдем его. Запишем полученную матрицу в виде системы уравнений:
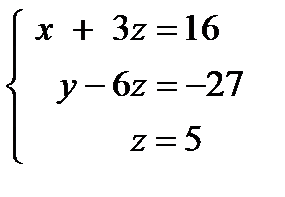. Отсюда 
.
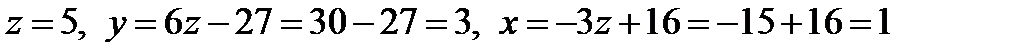Ответ: {(1, 3, 5)}.
Пример 2. Решить систему уравнений: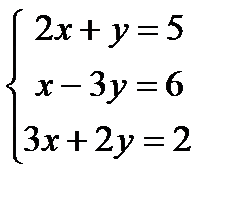 
.
Решение.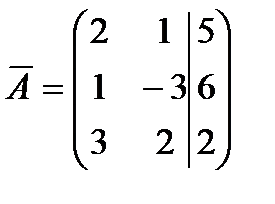 
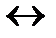
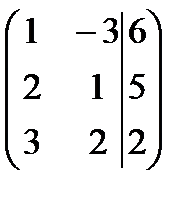
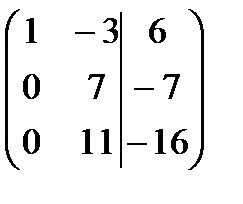
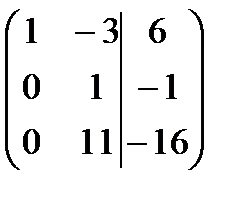
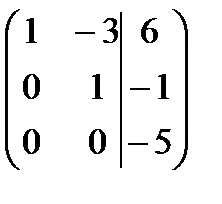. Проверим условия теоремы Кронекера-Капелли: 
то есть, 
, следовательно, система не имеет решений.
Ответ: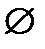 
.
Пп. 2. Метод Крамера
(для решения неоднородных систем, когда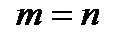 
)
Замечание. Метод применяется (редко) для решения и однородных систем, в случае, когда 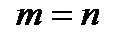. Будет рассмотрено в замечании к теореме Крамера.
Теорема Крамера. Рассмотрим неоднородную систему n линейных уравнений с n неизвестными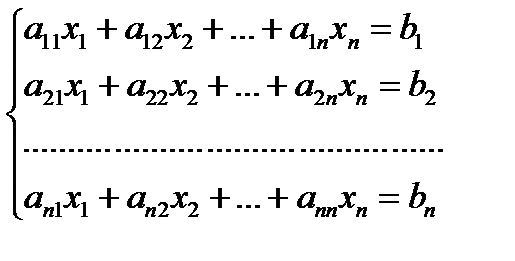 
. Если определитель матрицы системы отличен от нуля, то система имеет единственное решение, которое находится по формулам: 
, 
, …, 
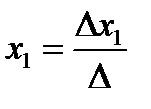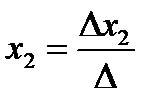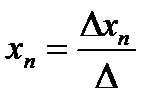, где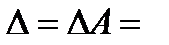 
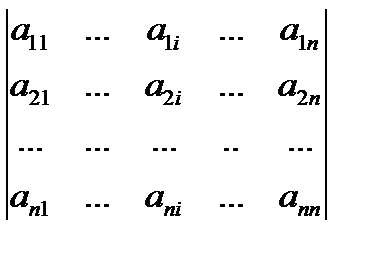– определитель матрицы системы, 
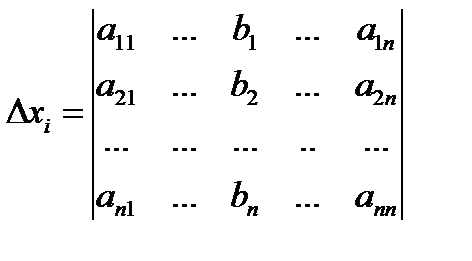– определитель, полученный из определителя 
заменой i –того столбца столбцом свободных членов, i = 1, 2,…, n. (без доказательства)
Замечание 1) Если определитель матрицы неоднородной системы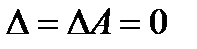 
, но и все 
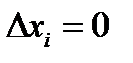, то система имеет бесконечное множество решений, которые находятся по формулам: 
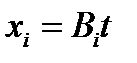, где В i – алгебраические дополнения к элементам той строки, где стоит элемент, минор которого отличен от нуля.
Если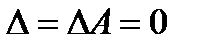 
, но при этом хотя бы один из 
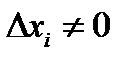, то система не имеет решений.
Замечание 2) Метод Крамера можно применить и для решения однородных систем линейных уравнений, когда .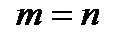
Если 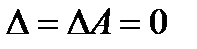, но хотя бы один из его миноров отличен от нуля, то система имеет бесконечное множество решений, которые находятся по формулам: 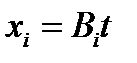, где В i – алгебраические дополнения к элементам той строки, где стоит элемент, минор которого отличен от нуля.
Если 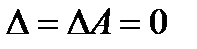и все его миноры равны нулю, то система сводится к одному уравнению и имеет бесконечное множество решений.
Если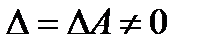 
, то система имеет единственное решение - нулевое.
Пример 1. Решить систему уравнений: .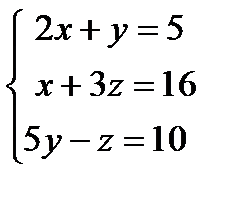
Решение. Найдем определитель матрицы системы: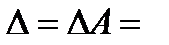 
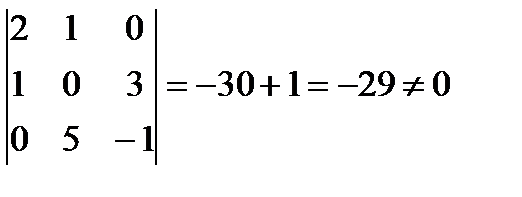, следовательно, система имеет единственное решение.
Найдем определители 
:
, 
, 
.
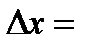
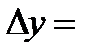
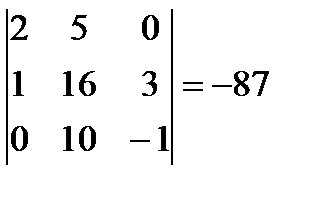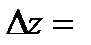
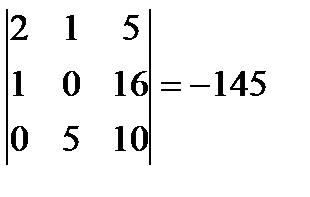Найдем решение системы по формулам Крамера:
, 
, 
.
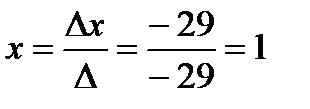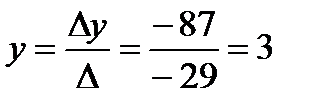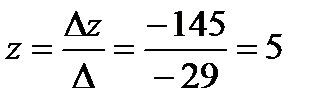Ответ: {(1, 3, 5)}.
Пример 2. Решить систему уравнений: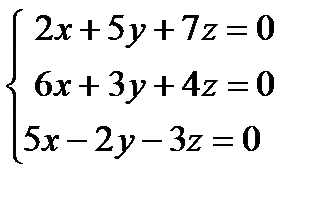 
.
Решение. Данная однородная система имеет 3 уравнения с тремя неизвестными. Для нахождения решения применим замечание 2 к теореме Крамера.
Найдем определитель матрицы системы: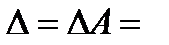 
, следовательно, система имеет единственное решение - нулевое.
Ответ: {(0, 0, 0)}.
Примеры.
Пример 1. Решить систему линейных уравнений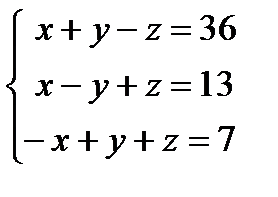 
двумя способами.
Решение.
1. Метод Гаусса.
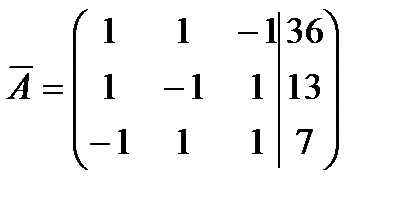
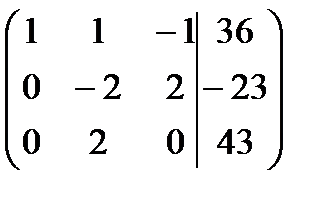
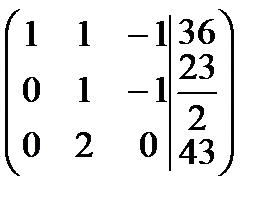
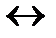
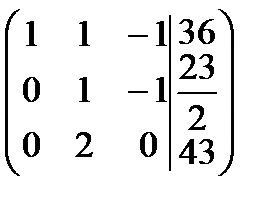
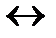
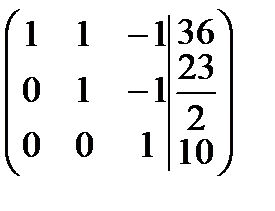
Найдем ранги матрицы системы и расширенной матрицы системы: 
, число неизвестных n = 3, следовательно,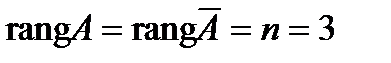 
, отсюда по теореме Кронекера-Капелли система имеет единственное решение.
Найдем его. Для этого запишем полученную матрицу в виде системы линейных уравнений:
.
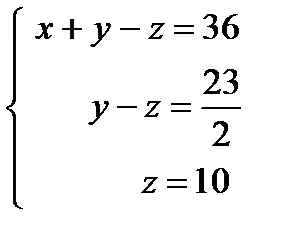Отсюда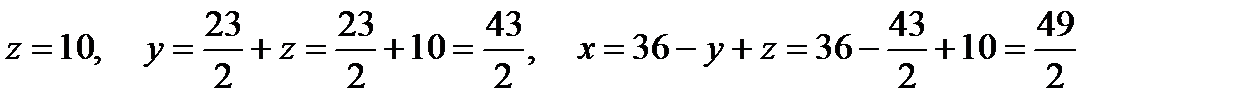 
.
Ответ: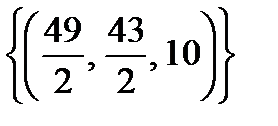 
.
2) Метод Крамера.
Найдем определитель матрицы системы: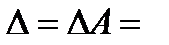 
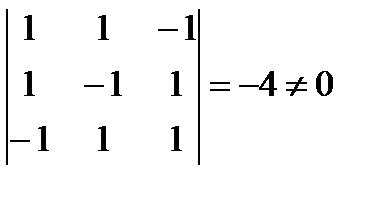, следовательно, существует единственное решение. Найдем определители :
, 
, 
.
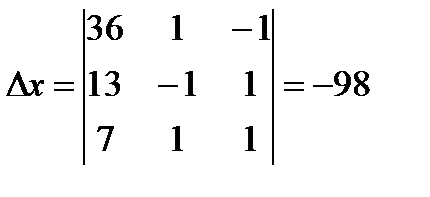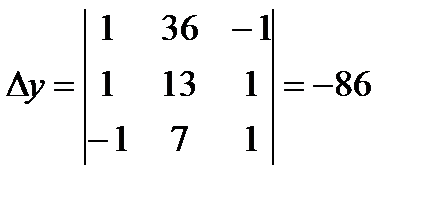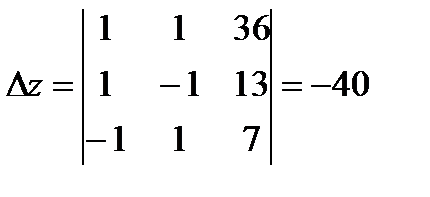По формулам Крамера решение системы имеет вид:
, 
, 
.
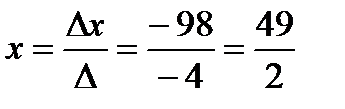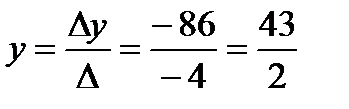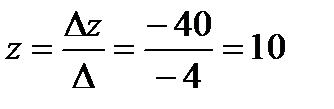Ответ: .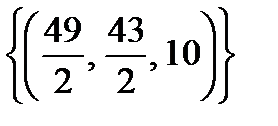
Пример 2. Решить систему линейных уравнений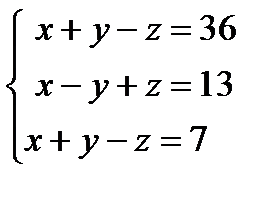 
методом Гаусса.
Решение.
1. Метод Гаусса.
.
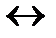
Найдем ранги матрицы системы и расширенной матрицы системы: 
, следовательно,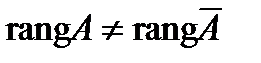 
, отсюда по теореме Кронекера-Капелли система не имеет решений.
Ответ: система не имеет решений.
Пример 3. Решить систему линейных уравнений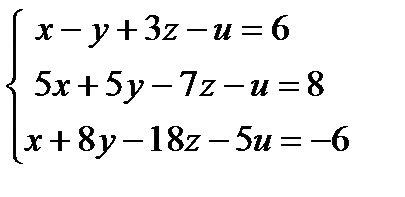 
.
В случае бесконечного множества решений, найти базисное решение.
Решение.
Данную систему можно решить только методом Гаусса, так как количество переменных больше, чем уравнений.
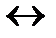
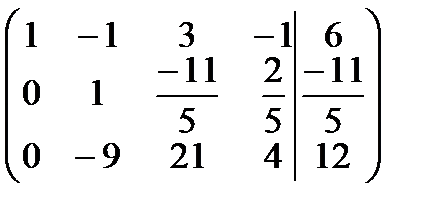
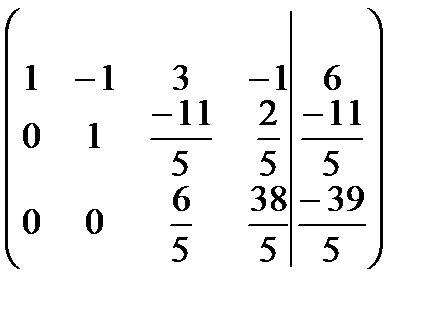
Найдем ранги матрицы системы и расширенной матрицы системы: 
, число неизвестных n = 4, следовательно,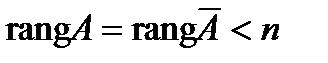 
, отсюда по теореме Кронекера-Капелли система имеет бесконечное множество решений. Найдем его. Для этого запишем полученную матрицу в виде системы уравнений:
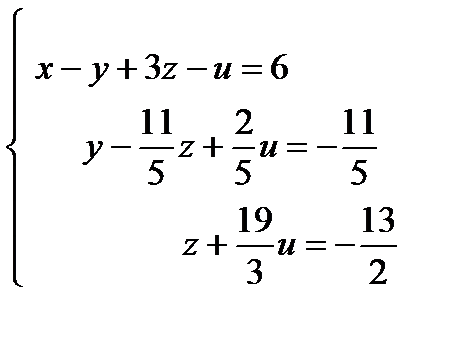
Введем одну свободную переменную, пусть это будет u, и выразим через нее все оставшиеся неизвестные.
, 
,
.
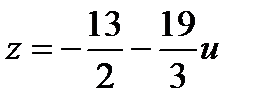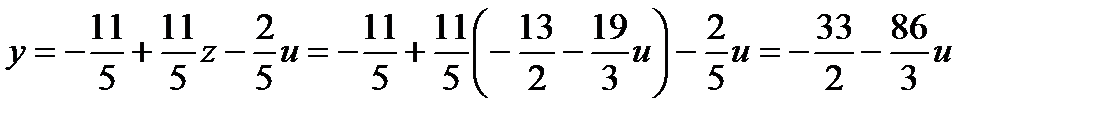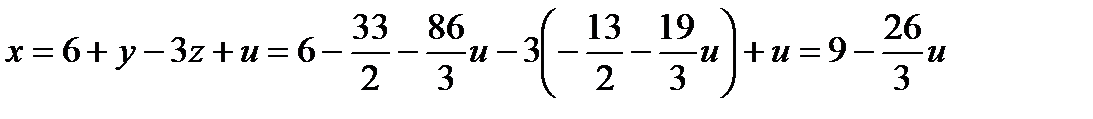Ответ: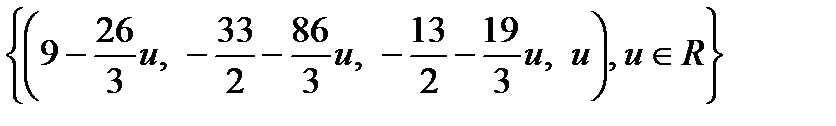 
. Базисным решением называется частное решение, получающееся из общего при нулевых значениях свободных переменных, то есть 
.
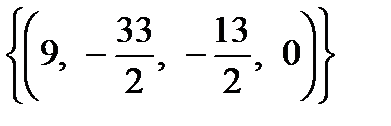Глава 2. Векторная алгебра.
Векторы.
П.1. Основные определения.
Существуют скалярные и векторные величины. Скалярные характеризуются своим численным значением (например, температура, работа, плотность,…), а векторные, кроме численного значения, обладают также направлением в пространстве (например, сила, скорость,…).
Определение 1. Вектором называется направленный отрезок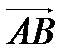 
с начальной точкой А и конечной В.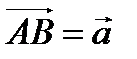 
| В |
|
| А |
Определение 2. Длиной вектора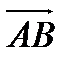 
называется длина отрезка 
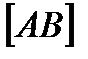. Число, равное длине вектора, измеренного выбранной масштабной единицей, называется модулем.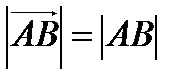 
Задать вектор – это значит задать его модуль и направление в пространстве.
Определение 3. Вектор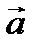 
называется единичным, если 
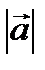=1. Вектор 
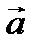называется нулевым или нуль-вектором, если 
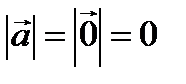. Нулевой вектор 
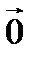имеет любое направление.
Определение 4. Векторы 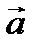и 
называются сонаправленными, если они параллельны (лежат на одной или параллельных прямых) и имеют одинаковое направление, если при этом направление не совпадает, то векторы называются противоположно направленными.
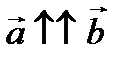– сонаправлены. 
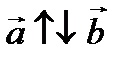– противоположно направлены.
Определение 5. Векторы 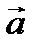и называются равными, если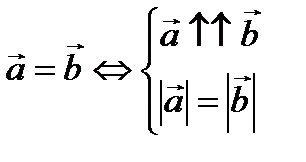 
.
Определение 6. Единичный вектор, имеющий одинаковое направление с вектором 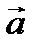, называется ортом вектора 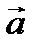и обозначается 
.
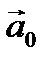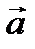
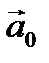
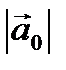=1.
Определение 7. Вектор, выходящий из начала координат, называется радиус-вектором.
С помощью параллельного переноса векторы можно перемещать в любое место пространства.
Дата: 2019-02-24, просмотров: 318.
