Определение 12. Проекцией вектора 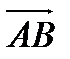 на ось l называется длина вектора
на ось l называется длина вектора 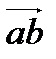 этой оси, заключенного между проекциями a и b его начальной точки А и конечной точки В, взятая со знаком «плюс», если направление
этой оси, заключенного между проекциями a и b его начальной точки А и конечной точки В, взятая со знаком «плюс», если направление 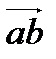 совпадает с направлением оси l, и со знаком «минус», если эти направления противоположны.
совпадает с направлением оси l, и со знаком «минус», если эти направления противоположны.
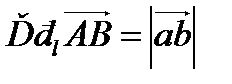
| В |
| А |
| С |
| l |
| а |
| b |
| D |
| c |
| d |
| α |
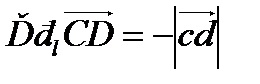
Замечание. Проекцией точки А на ось l называется точка А0 такая, что прямая (АА0) пересекает ось l под углом 900 в точке А0.
Теоремы о проекциях:
Теорема 2.  , где α – угол между вектором
, где α – угол между вектором  и положительным направлением оси l.
и положительным направлением оси l.
Теорема 3. 
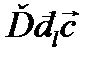 . Проекция ломаной равна проекции замыкающего контура.
. Проекция ломаной равна проекции замыкающего контура.
Теорема 4. 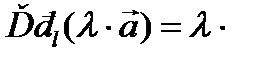
 . (без доказательства)
. (без доказательства)
| x1 |
| x2 |
| y1 |
| y2 |
| z1 |
| z2 |
| x |
| y |
| z |
| ax |

|
| ay |
| az |
| A |
| B |
| O |
Определение 13. Проекции вектора на координатные оси называются координатами вектора.
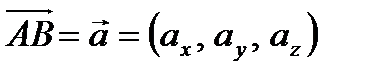 ,
, 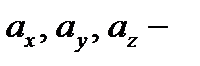 координаты вектора
координаты вектора 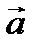 .
.
Если даны координаты точек A(x1, y1, z1), B(x2, y2, z2), то
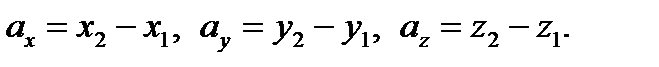
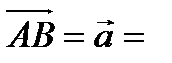
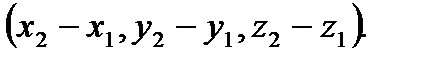
Длина вектора находится по формуле:
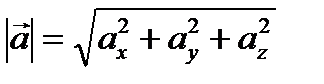 .
.
Следствие из теоремы 1. Вектор 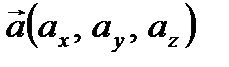 коллинеарен вектору
коллинеарен вектору 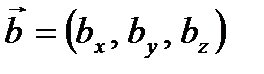 тогда и только тогда, когда их координаты пропорциональны:
тогда и только тогда, когда их координаты пропорциональны: 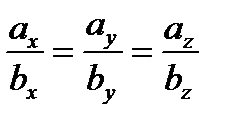 .
.
Замечание 1. 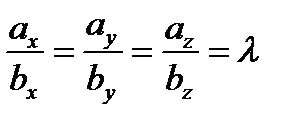 , где λ – коэффициент пропорциональности. Если λ > 0, векторы сонаправлены (
, где λ – коэффициент пропорциональности. Если λ > 0, векторы сонаправлены ( 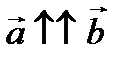 ); λ < 0, векторы противоположно направлены (
); λ < 0, векторы противоположно направлены ( 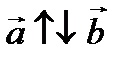 ).
).
Замечание 2. 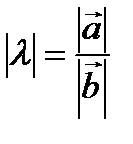 .
.
Ортами координатных осей (Ох), (О y), (О z) называются векторы  соответственно.
соответственно.  .
.
| α |
| β |
| γ |
| x |
| y |
| z |
| ax |

|
| ay |
| az |
| A |
| B |
| O |
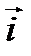
|
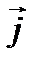
|
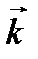
|
 , построенный на векторах
, построенный на векторах 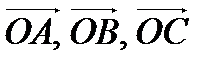 (по правилу параллелепипеда), причем
(по правилу параллелепипеда), причем 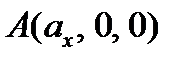 ,
,  ,
, 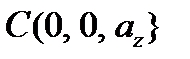 :
: 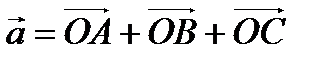 (*).
(*).
Так как 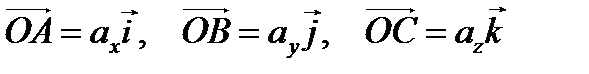 , то подставив в (*), получим
, то подставив в (*), получим
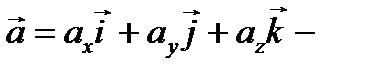 разложение вектора
разложение вектора 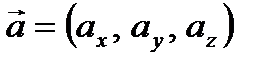 по ортам
по ортам  .
.
Пусть α, β, γ – углы между вектором  и координатными осями, тогда в силу теоремы 2 получим, что
и координатными осями, тогда в силу теоремы 2 получим, что 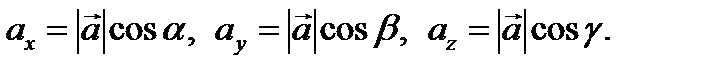
Определение 14. Направляющими косинусами вектора 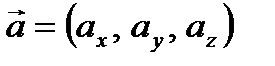 называются
называются 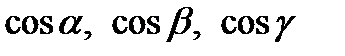 , где α, β, γ – углы между вектором
, где α, β, γ – углы между вектором 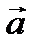 и координатными осями, причем
и координатными осями, причем 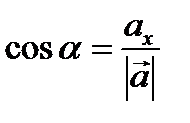 ,
,  ,
, 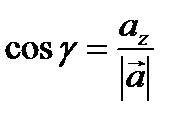 .
.
Замечание. Из определения видно, что направляющие косинусы являются координатами орта вектора  , т.е.
, т.е. 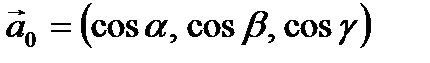 .
.
Определение 15. Нормой вектора в евклидовом пространстве называется длина вектора.
Определение 16. Орт вектора называется нормированным вектором.
Теорема 5 (о направляющих косинусах). Сумма квадратов направляющих косинусов равна 1:
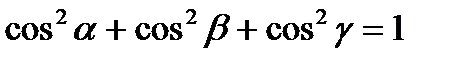 .
.
Доказательство (для плоского случая)
| ах |
| ау |
| х |
| у |
| О |
| α |
| β |
|
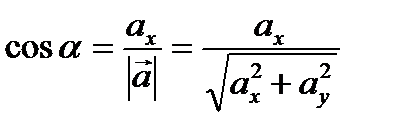 ,
, 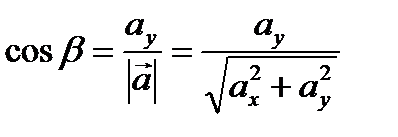 .
.
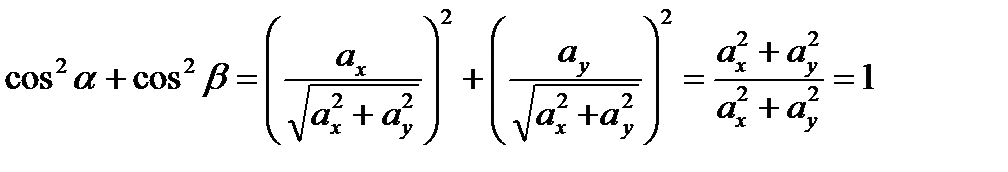 , что и треб. доказать.
, что и треб. доказать.
Определение 17. Даны два вектора 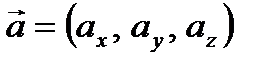 и
и 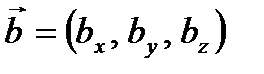 , тогда координаты вектора их суммы и разности вычисляются по формулам:
, тогда координаты вектора их суммы и разности вычисляются по формулам:
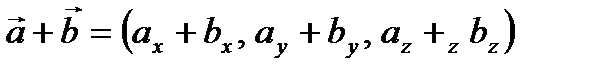 ,
,  .
.
Определение 18. Произведением вектора  на действительное число λ называется вектор
на действительное число λ называется вектор  такой, что
такой, что  .
.
Замечание. Для вектора  n-мерного пространства справедливы все определения и теоремы.
n-мерного пространства справедливы все определения и теоремы.
Пример. Даны точки М1(2; 1), М2(–1;3) и вектор 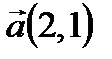 . Найти длину и направление вектора
. Найти длину и направление вектора 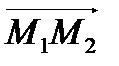 , координаты его орта, проверить коллинеарность векторов
, координаты его орта, проверить коллинеарность векторов 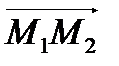 и
и 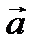 , найти координаты вектора
, найти координаты вектора 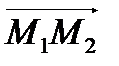 – 2
– 2 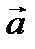 .
.
Решение.
Найдем координаты вектора 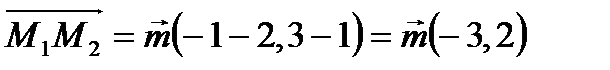 .
.
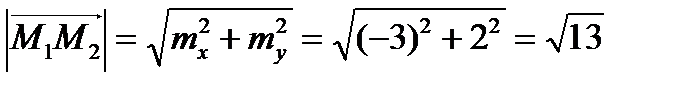 .
.
Найдем направляющие косинусы: 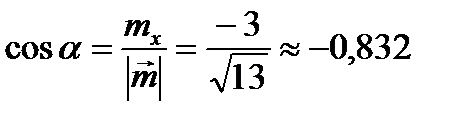 ,
, 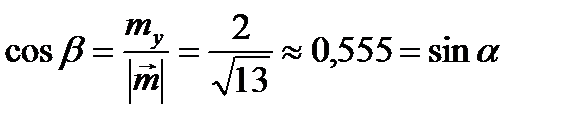 . Отсюда,
. Отсюда, 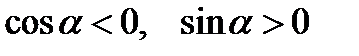 , следовательно,
, следовательно, 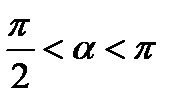 ,
, 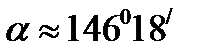 .
.
Координаты орта по замечанию к определению 14: 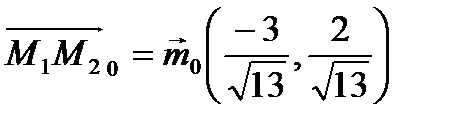 . Вектор называется нормированным вектором.
. Вектор называется нормированным вектором.
По следствию к теореме 1 проверим коллинеарность векторов: для коллинеарности должно выполняться условие 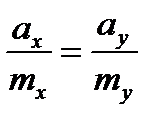 . Проверим:
. Проверим: 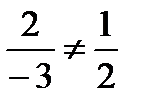 , следовательно,
, следовательно, 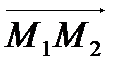 и
и 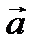 не коллинеарны.
не коллинеарны.
Найдем координаты вектора 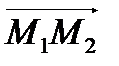 – 2
– 2 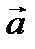 . Координаты вектора
. Координаты вектора 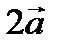 найдем по определению 18:
найдем по определению 18: 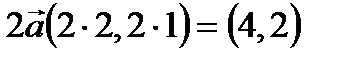 , тогда по определению 15:
, тогда по определению 15: 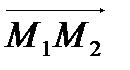 – 2
– 2 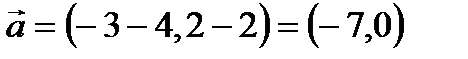 .
.
Дата: 2019-02-24, просмотров: 366.