Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

 

Определение. Уравнение вида 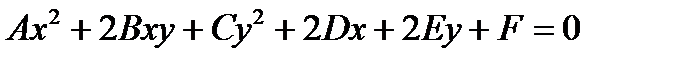, где А, В, С одновременно не равны нулю, называется общим уравнением кривой второго порядка.

Этому уравнению не всегда соответствует на плоскости множество точек. Если геометрический образ не существует, то есть, нет точек, удовлетворяющих уравнению, то говорят, что уравнение определяет мнимую кривую.

Из общего уравнения получаются многочисленные уравнения кривых – канонические уравнения. Ограничимся констатацией того, что уравнение в зависимости от коэффициентов может задавать только четыре типа кривых, а именно, окружность, эллипс, гиперболу и параболу, причем, если 1) 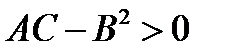, то это уравнение эллипса (действительного или мнимого) или точки, в случае А = В – окружность; 2) , то это уравнение гиперболы или двух пересекающихся прямых;                            3) 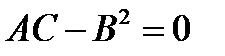, то это уравнение параболы или пары прямых.

Если В = 0, то уравнение называется пятичленным уравнением кривой второго порядка. Приведение такого уравнение к каноническому виду осуществляется путем образования полных квадратов по отношению к переменным х и у: 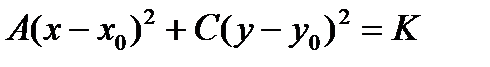 и параллельному переносу начала координат в точку (х₀, у₀). Если 1) 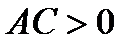, то это уравнение эллипса (действительного или мнимого) или точки; 2) 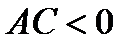, то это уравнение гиперболы или двух пересекающихся прямых; 3) , то это уравнение параболы или пары прямых.

Канонические уравнения основных кривых второго порядка.

1.     – уравнение эллипса

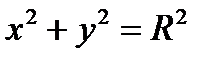    – уравнение окружности

2. 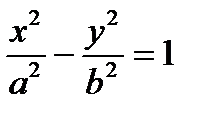,  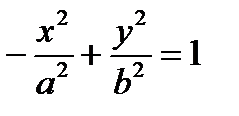  – уравнения гиперболы

3. 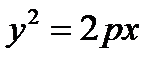, , 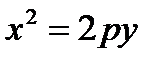,  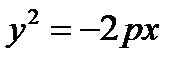  – уравнения параболы (р > 0)

4. 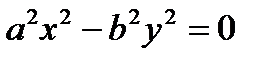,  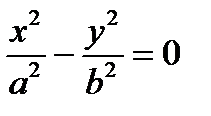  – пара пересекающихся прямых

5. 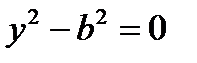,  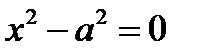   – уравнения параллельных прямых

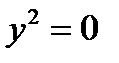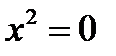,    – уравнения совпадающих прямых

6. 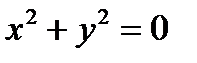   – точка О(0,0)

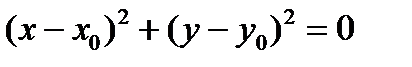    – точка М₀(х₀,у₀)

Окружность

Определение. Окружностью называется геометрическое место точек плоскости, равноудаленных от фиксированной точки, называемой центром окружности.

Теорема. Окружность радиуса R с центром в точке  имеет уравнение  

(1)

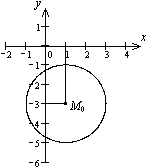Любое уравнение окружности с помощью тождественных преобразований можно привести к каноническому виду (1). Для этого достаточно выделить полные квадраты по переменным и у.

Пример. Нарисуйте кривую .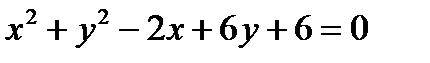

 Решение. Сгруппируем .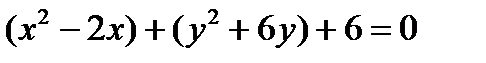

Выделим полные квадраты, получим:     .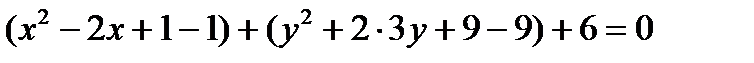

Отсюда ,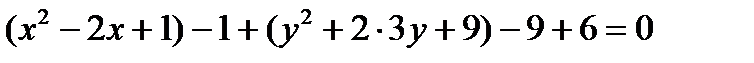

                                .

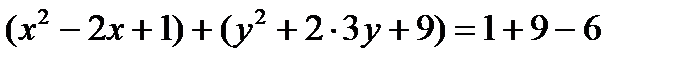 Тогда каноническое уравнение имеет вид: .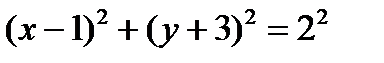  

Итак, центр окружности -точка М₀(1,-3), радиус равен 2.

 

 

Эллипс

Определение. Эллипсом называется геометрическое место точек плоскости, для каждой из которых сумма расстояний до двух данных точек F₁  и F₂ той же плоскости, называемых фокусами эллипса, есть величина постоянная и равная 2а.

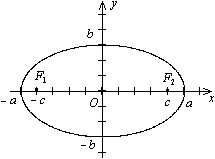Начало О системы координат расположим на середине отрезка F₁F₂. Координаты фокусов F₁(-с,0), F₂(с,0).  

Тогда расстояние между фокусами равно 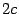:  |F₁F₂|=2c.

Ось 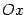направим вдоль этого отрезка, ось Oy перпендикулярна к этому отрезку.

Теорема. В выбранной системе координат эллипс имеет каноническое уравнение

(2),   где        или

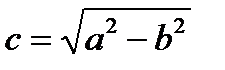
Свойства эллипса: Эллипс обладает двумя взаимно перпендикулярными осями симметрии, на одной из которых находятся его фокусы, и центром симметрии. Если эллипс задан каноническим уравнением (2), то его осями симметрии служат оси 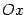и Оу, начало координат - центр симметрии.

Построение эллипса.  Строим две окружности с центром в точке О радиусами а и b.                       (a > b).Строим луч, выходящий из начала координат до пересечения с обеими окружностями. Из точек пересечения опускаем пересекающиеся лучи, параллельные координатным осям. Точка пересечения данных лучей – это очка, принадлежащая эллипсу.

Определения. Точки пересечения эллипса с его осями симметрии называются вершинами эллипса, центр симметрии - центром эллипса, отрезок между двумя вершинами, содержащий фокусы, называется большой осью эллипса, половина его длины - большой полуосью эллипса.

 Если эллипс задан каноническим уравнением , то его вершины имеют координаты      (-а,0), (а,0), (0,b), (0,-b) , большая полуось равна 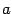, малая полуось равна .

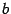Величина  называется эксцентриситетом эллипса. Величина 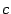, являющаяся половиной расстояния между фокусами, определяется из формулы 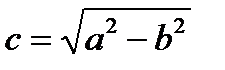. Эксцентриситет  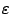эллипса характеризует степень вытянутости эллипса. Чем ближе экcцентриситет к нулю, тем больше эллипс похож на окружность. Чем ближе эксцентриситет к 1, тем сильнее вытянут эллипс. Отметим, что по определению для эллипса .  

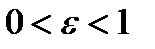Прямые, между которыми вытянут эллипс, называются директрисами, уравнения которых .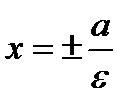

Замечание 1.Уравнение (2) было получено в предположении, что  F₁ и F₂ - различные точки, то есть c > 0. Тогда b < a. Но кривую, определяемую уравнением, можем рассмотреть и в случае 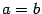, (c = 0). Уравнение в этом случае после умножения на  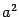примет вид 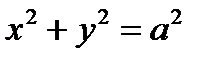. Это уравнение окружности радиуса  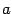с центром в начале координат. Таким образом, можно рассматривать окружность как предельный вариант эллипса, когда 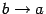, , 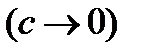или, как иногда говорят математики, окружность является "вырожденным" эллипсом, у которого фокусы совпали.

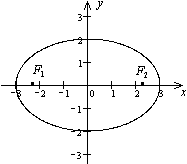Замечание 2. Если 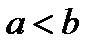, то фокусы лежат на оси (Оу) и имеют координаты F₁(0,-с), F₂(0,с), где 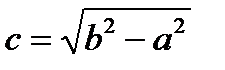. Эксцентриситет 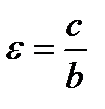. Уравнения директрис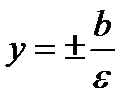

Замечание 3. Если центр эллипса лежит в точке М₀(х₀,у₀), то каноническое уравнение эллипса примет вид: 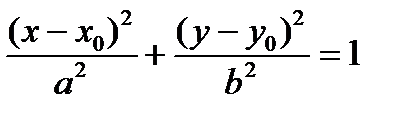. Уравнения директрис 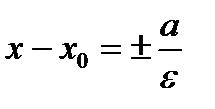, координаты фокусов F₁(х₀–с, у₀), F₂((х₀+с, у₀).

Пример 1. Постройте кривую 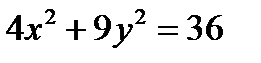. Найдите фокусы и эксцентриситет.

Решение. Разделим обе части уравнения на 36. Получаем уравнение 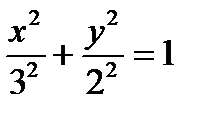. Это каноническое уравнение эллипса, 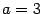, 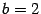.  Из соотношения находим 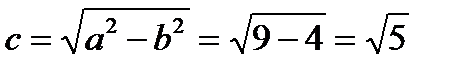, фокусы F₁( 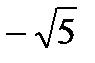, 0), F₂( , 0), эксцентриситет .

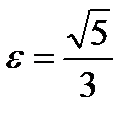Пример 2. Найдите фокусы и эксцентриситет эллипса .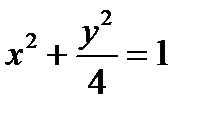

Решение. Уравнение запишем в ви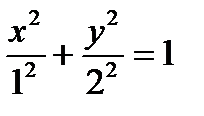де , где 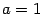, , 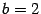b > a. Отсюда 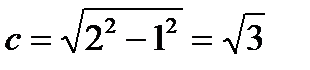. Фокусы имеют координаты F₁( 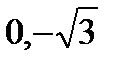), F₂( 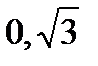). Эксцентриситет равен . 

Гипербола .

Из школьного курса математики известно, что кривая, задаваемая уравнением 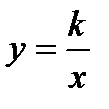, где 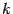– число, называется гиперболой. Однако это - частный случай гиперболы (равносторонняя гипербола).

Определение. Гиперболой называется геометрическое место точек плоскости, для каждой из которых абсолютная величина разности расстояний до двух фиксированных точек F₁  и F₂ той же плоскости, называемых фокусами гиперболы, есть величина постоянная равная 2а.

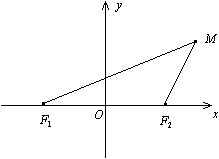
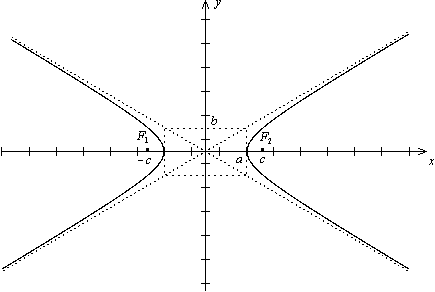Теорема. Пусть расстояние между фокусами гиперболы равно 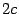, т.е. фокусы имеют координаты F₁(-с,0), F₂(с,0), тогда в выбранной системе координат гипербола имеет уравнение           (3), где 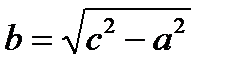        или .

 

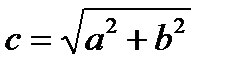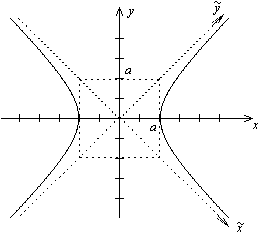
Свойство. Гипербола обладает двумя взаимно перпендикулярными осями симметрии, на одной из которых лежат фокусы гиперболы, и центром симметрии. Если гипербола задана каноническим уравнением (3), то ее осями симметрии служат координатные оси и Оу, а начало координат - центр симметрии гиперболы.

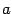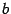Определения. Точки пересечения гиперболы, заданной каноническим уравнением (3), с осью называются вершинами гиперболы, отрезок между ними называется действительной осью гиперболы. Отрезок оси ординат между точками (0, -b) и (0,b) называется мнимой осью. Числа и называются соответственно действительной и мнимой полуосями гиперболы. Начало координат называется ее центром.

Величина   называется эксцентриситетом гиперболы. Величина с > a, то есть у гиперболы 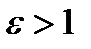. Эксцентриситет 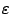характеризует угол между асимптотами, чем ближе 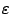к 1, тем меньше этот угол.

Прямые , к которым график гиперболы приближается, но не пересекает, называются асимптотами гиперболы. Уравнения директрис .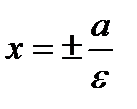

Построение гиперболы. Чертим основной прямоугольник, т.е. прямоугольник с центром в начале координат со сторонами 2a и  2b, диагоналями которого будут асимптотами гиперболы (см. рис. выше в определении).

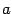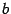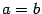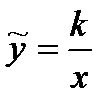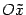Замечание 1. В отличие от эллипса в каноническом уравнении гиперболы соотношение между величинами и  может быть произвольным. В частности, при  мы получим равностороннюю гиперболу, известную из школьного курса математики. Ее уравнение имеет знакомый вид , если взять , а оси и  направить по биссектрисам четвертого и первого координатных углов (рис.).

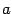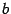Замечание 2. Если каноническое уравнение гиперболы имеет вид  (3*), то ее фокусы располагаются на оси Оу, их координаты F₁(0,-с), F₂(0,с), числа и называются соответственно мнимой и действительной полуосями гиперболы; уравнения асимптот 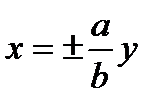, уравнения директрис 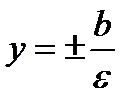. (См. рис. примера 2)

Вообще говоря, данное уравнение (3*) не является каноническим, так как знаки перед 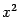и у² противоположны знакам в первом каноническом уравнении (3). Но, если переобозначить переменные, т.е. взять 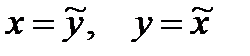, то получим снова каноническое уравнение (3): 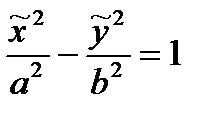. В связи с этим уравнение (3*) будем сразу называть каноническим.

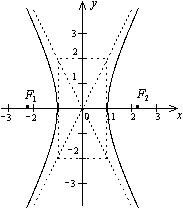Замечание 3. Если центр гиперболы смещен и лежит в точке М₀(х₀,у₀), то каноническое уравнение гиперболы примет вид: (или 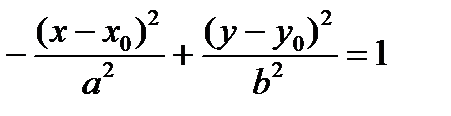). Тогда координаты фокусов F₁(х₀-с, у₀), F₂(х₀+с, у₀), уравнения асимптот 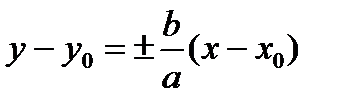, уравнения директрис .

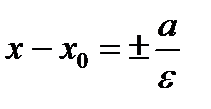Пример 1. Постройте гиперболу 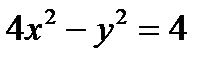, найдите ее фокусы и эксцентриситет.

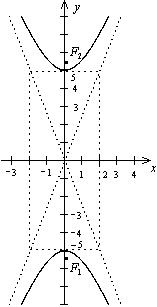Решение. Разделим обе части уравнения на 4. Получим каноническое уравнение , , 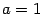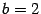. Проводим асимптоты 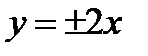и строим гиперболу. Из формулы получим 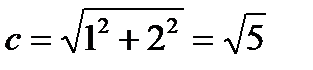. Тогда фокусы , эксцентриситет .

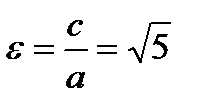Пример 2. Постройте гиперболу 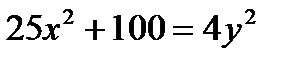. Найдите ее фокусы и эксцентриситет.

Решение. Преобразуем уравнение к виду 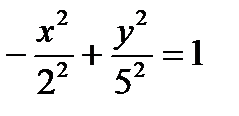. Фокусы гиперболы лежат на оси (Оу), действительная полуось b = 5, мнимая а = 2. Асимптоты имеют уравнение 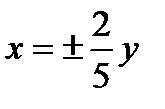. Из формулы получим 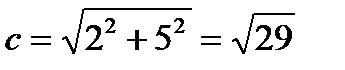, эксцентриситет 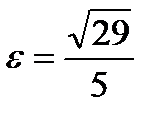, координаты фокусов .

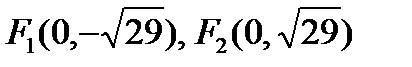Парабола

В школьном курсе математики достаточно подробно изучалась парабола, которая, по определению, являлась графиком квадратного трехчлена. Здесь мы дадим другое (геометрическое) определение параболы.

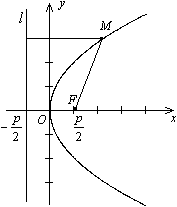Определение. Параболой называется геометрическое место точек плоскости, для каждой из которых расстояние до фиксированной точки F этой плоскости, называемой фокусом, равно расстоянию до фиксированной прямой, лежащей в той же плоскости и называемой директрисой параболы.

 

Чтобы получить уравнение кривой, соответствующей этому определению, введем подходящую систему координат. Пусть расстояние между фокусом 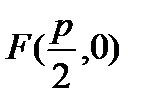 и директрисой параболы l, уравнение которой 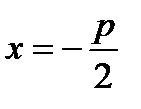,  равно p ( .

 

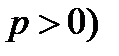Теорема. В выбранной системе координат парабола имеет уравнение 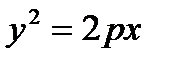. (4)

Уравнение (4) называется каноническим уравнением параболы.

Замечание. Парабола обладает осью симметрии. Если парабола задана каноническим уравнением, то ось симметрии совпадает с осью 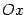. Асимптот парабола не имеет.

Определение. Точка пересечения оси симметрии с параболой называется вершиной параболы.

Построение. Проведем прямую 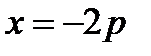. Выберем на ней произвольным образом точку М. Проведем через точку М луч (ОМ) и луч, параллельный оси Ох. Проведем луч, выходящий из начала координат перпендикулярно лучу (ОМ) до пересечения с лучом, параллельным оси Ох. Точка их пересечения принадлежит параболе.