1)
| В |
| А |
|
|
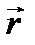
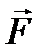
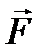приложена к точке В. Тогда моментом силы 
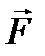относительно точки А называется вектор 
такой, что 
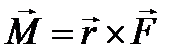, где вектор 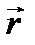- плечо АВ, 
.
2) Пусть материальная точка движется по окружности с центром в точке О,
|
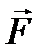
| M |
| O |
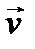- линейная скорость движения точки, 
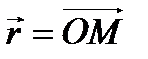- радиус-вектор точки М. Тогда угловой скоростью материальной точки называется вектор 
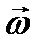такой, что 
.
|
|
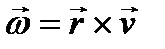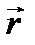
Свойства векторного произведения.
1. 
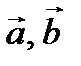– коллинеарные векторы либо один из них является нулевым.
Частный случай: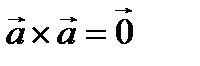 
2. 
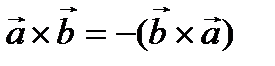(Пояснение: из-за смены троек)
3. Если 
– действительное число, то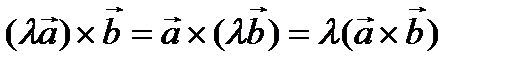 
(Пояснение: если одну из сторон параллелограмма увеличить в λ раз, не меняя ее направление, то и площадь увеличиться в λ раз).
4. 
, 
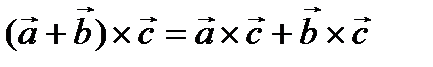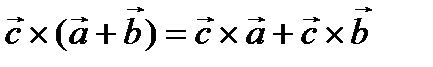Перемножаем, строго соблюдая порядок.
Таблица векторного умножения ортов
|
|
|
|
|
|
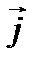
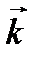
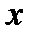
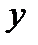
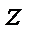
| 1 |
| 1 |
| 1 |
| O |
, 
, 
, 
, 
,
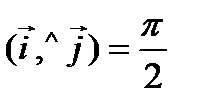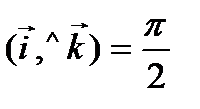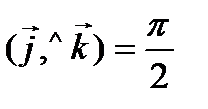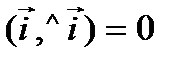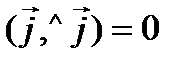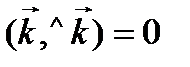; тогда 
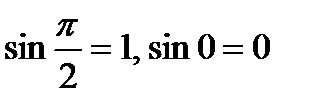; длины ортов равны 
.
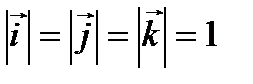Следовательно, исходя из определения векторного произведения, можем записать, что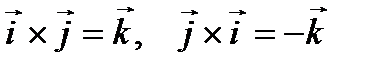 
, 
, 
, 
.
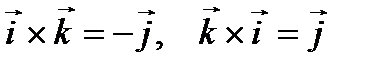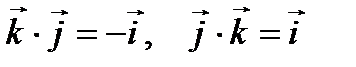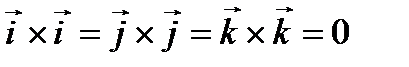Векторное произведение векторов, заданных своими декартовыми координатами
Два вектора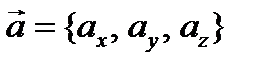 
и 
заданы своими декартовыми координатами. Разложим их по ортам 
: 
, 
.
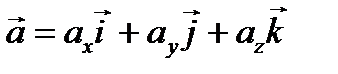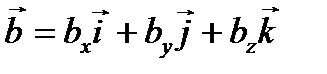Найдем векторное произведение данных векторов:
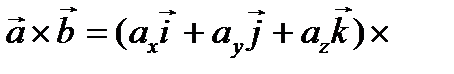
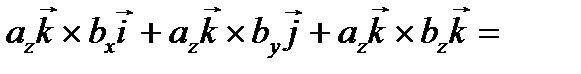(воспользуемся таблицей векторного умножения ортов и сгруппируем) = =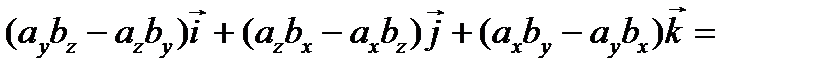 
.
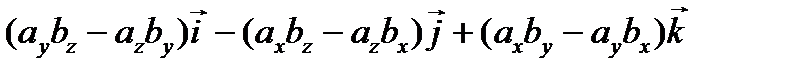Выражения в скобках получаются при вычислении определителей 2-го порядка, поэтому можно записать: 
– разложение по первой строке определителя 3-го порядка:
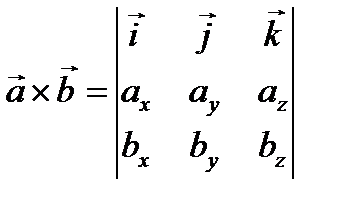– (4)
формула для нахождения векторного произведения векторов, заданных своими декартовыми координатами.
Можем записать, что координаты вектора векторного произведения равны:
.
Примеры.
Пример № 1. Векторы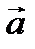 
и 
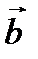образуют угол 
. Зная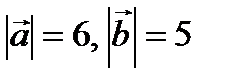 
, вычислить 
.
Решение.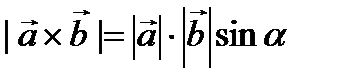 
= 
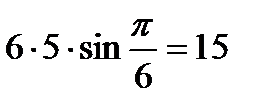. Ответ: 15.
Пример № 2. Даны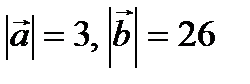 
, 
. Вычислить 
.
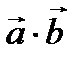Решение. Из свойства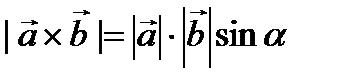 
выразим 
.
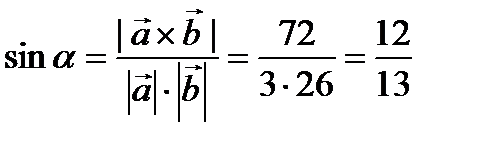Из основного тригонометрического тождества следует, что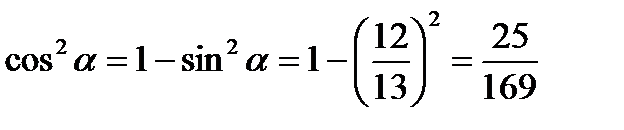 
.
Найдем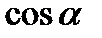 
: 
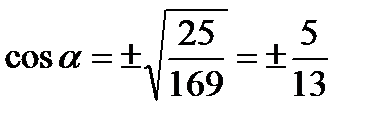. По определению найдем скалярное произведение векторов: 
= 
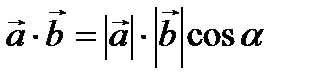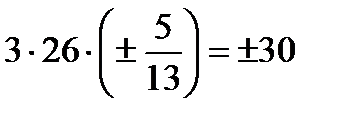
Пример № 3. Векторы 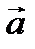и 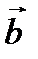образуют угол 
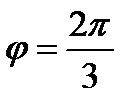. Зная 
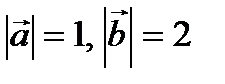, вычислить 
.
Решение.
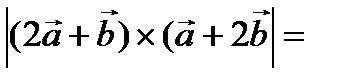
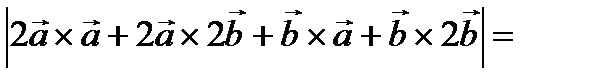
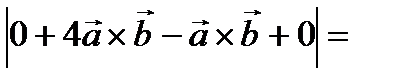
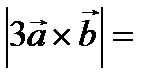3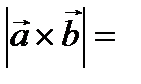 
= 
.
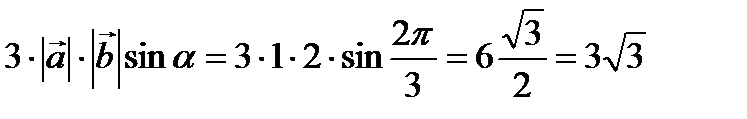Пример № 4. Даны два вектора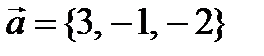 
и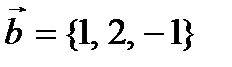 
. Найти координаты векторного произведения векторов 
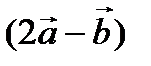и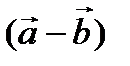 
.
Решение.
Найдем координаты векторов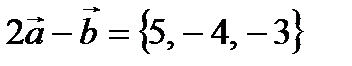 
, 
.
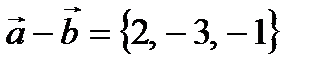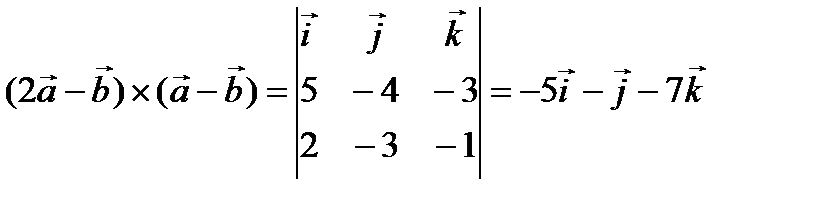. Ответ: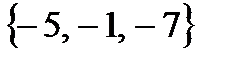 
Пример № 5. Сила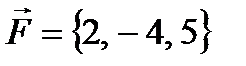 
приложена к точке В(4, -2, 3). Определить момент этой силы относительно точки А(3, 2, -1) и его величину.
Решение.
Найдем вектор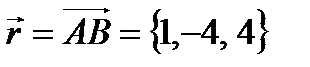 
.
= 
.
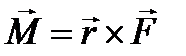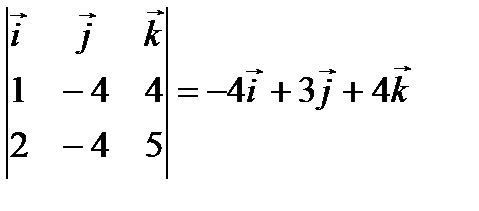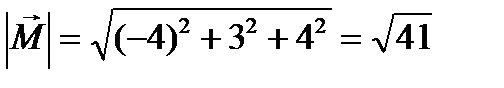. Ответ: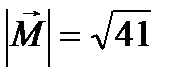 
Пример № 6. Даны три вершины параллелограмма ABCD: А(2, -1, 2), В(1, 2, -1), С(3, 2, 1). Найти его площадь.
Решение.
Найдем векторы, на которых построен параллелограмм: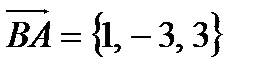 
, 
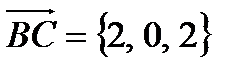(они должны выходить из одной точки).
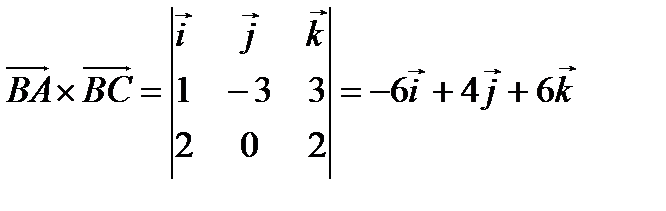. Тогда 
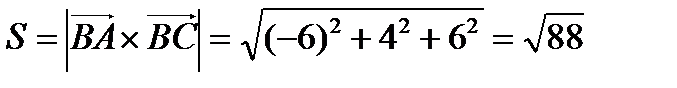ед.кв..
§ 4. Смешанное произведение векторов
Определение. Смешанным или векторно-скалярным произведением трех векторов называется число, равное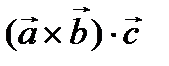 
.
|
|
|
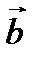
по определению = 
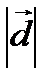Пр 
.
|
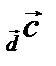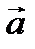
, а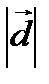 
- площадь параллелограмма, построенного на векторах
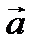и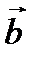 
. Вектор 
по определению векторного произведения перпендикулярен к векторам 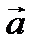и 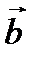, следовательно, перпендикулярен плоскости параллелограмма. Построим на векторах 
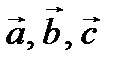параллелепипед. Тогда Пр 
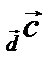- это высота данного параллелепипеда: Пр 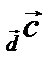= h. Из всего вышесказанного получили, что 
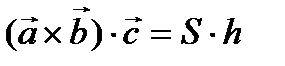= V – объем параллелепипеда, причем 
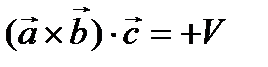, если 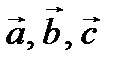образуют правую тройку (h > 0), и 
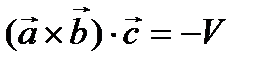, если левую (h < 0). В связи с чем, правильнее писать, что объем параллелепипеда, построенного на векторах 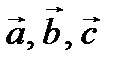равен 
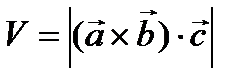. (1)
Свойства смешанного произведения.
1. 
При циклической перестановке множителей смешанное произведение не изменяется.
Данное свойство позволяет ввести новое обозначение смешанного произведения: 
, так как результат не зависит, как расставляются скобки.
2. Условие компланарности трех векторов:
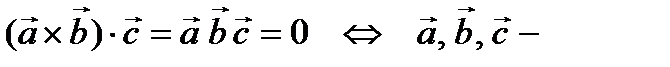компланарные векторы. (2)
Т.е. параллелепипед вырождается в часть плоскости с нулевым объемом.
3. 
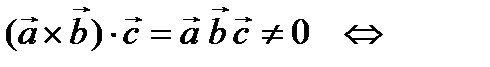
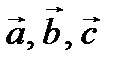образуют базис во множестве векторов. (3)
Дата: 2019-02-24, просмотров: 353.
