1. Лемниската Бернулли 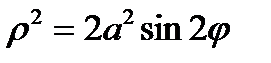 ,
, 
2. Спираль Архимеда 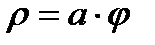
3. Логарифмическая спираль  ,
, 
4. Циссоида Диокла 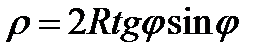 или
или 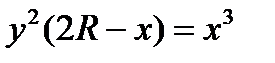
5. Кардиоида 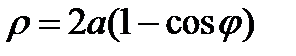 или
или 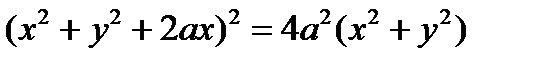
6. Астроида  или
или 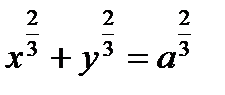
7. Циклоида 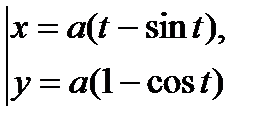 или
или 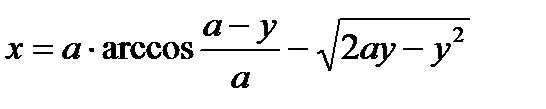
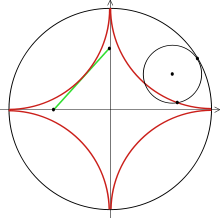
Спираль Архимеда Циссоиды

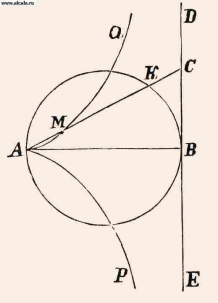 или
или 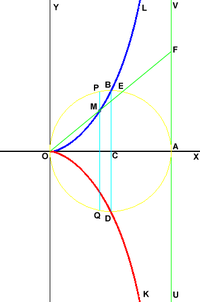 синяя и красная линии –
синяя и красная линии –
ветви циссоиды
Кардиоида Астроида Циклоида
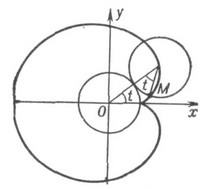

П. 5. Уравнения прямой на плоскости.
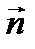
|
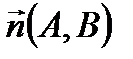 ):
): 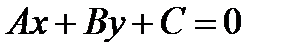 . (1)
. (1)
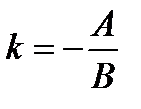 - угловой коэффициент
- угловой коэффициент
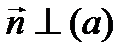
2. Уравнение прямой, проходящей через данную точку 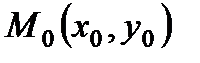 с заданным нормальным вектором
с заданным нормальным вектором  :
: 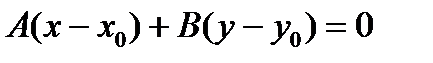 . (2)
. (2)
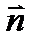
|
| М0 |
| М |
Вывод: Рассмотрим текущую точку прямой 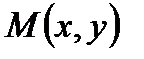 . Тогда вектор
. Тогда вектор 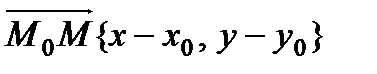 лежит на данной прямой. Следовательно, векторы
лежит на данной прямой. Следовательно, векторы 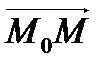 и
и 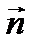 будут перпендикулярны:
будут перпендикулярны: 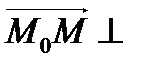
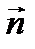 , то есть их скалярное произведение равно нулю
, то есть их скалярное произведение равно нулю 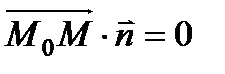 . Найдем скалярное произведение векторов, заданных своими декартовыми координатами:
. Найдем скалярное произведение векторов, заданных своими декартовыми координатами: 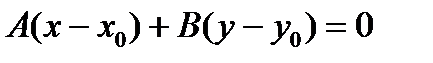 – (2). Если раскроем скобки, то получим общее уравнение прямой – (1).
– (2). Если раскроем скобки, то получим общее уравнение прямой – (1).
3. Уравнение прямой, проходящей через данную точку  с заданным угловым коэффициентом k:
с заданным угловым коэффициентом k:
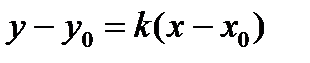 , (3)
, (3)
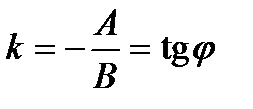 ,
, 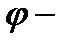 угол между осью Ох (положительным направлением) и прямой.
угол между осью Ох (положительным направлением) и прямой.
Расположение двух прямых
1) Условие параллельности двух прямых:  (координаты пропорциональны
(координаты пропорциональны  ) или
) или 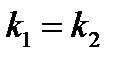 .
.
2) Условие перпендикулярности двух прямых:  (
( 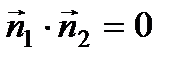 ) или
) или  .
.
3) Угол между прямыми 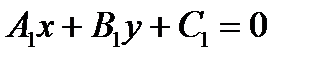 и
и 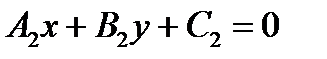
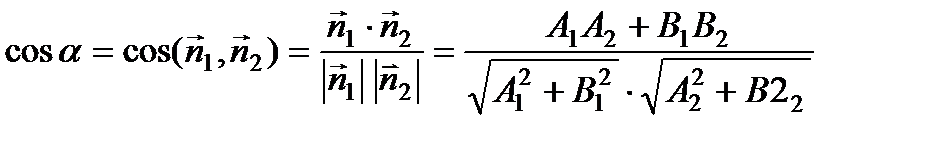 или
или 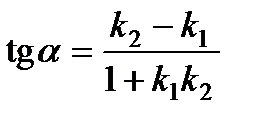
Точка пересечения прямых находится как: 
4. Уравнение прямой, проходящей через две заданные точки 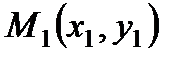 и
и 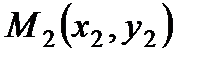 :
:
 . (4)
. (4)
5. Уравнение прямой в отрезках: 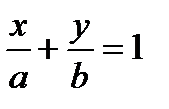 , (5)
, (5)
где a и b – величины направляющих отрезков, отсекаемых прямой на координатных осях (Ох) и (Оу) соответственно.
6. Каноническое уравнение прямой 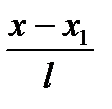
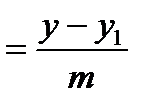 , (6)
, (6)
т.е. уравнение прямой, проходящей через данную точку 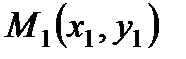 параллельно заданному вектору
параллельно заданному вектору 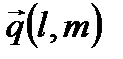 .
.
 – направляющий вектор прямой.
– направляющий вектор прямой.
7. Параметрические уравнения прямой 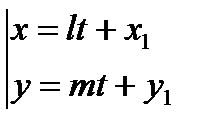 , (7)
, (7)
т.е. уравнение прямой с параметром t, проходящей через данную точку 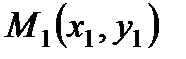 параллельно заданному вектору
параллельно заданному вектору  .
.
Нормальное уравнение прямой
| у |
| х |
| р |
| α |
| β |
| (а) |
| О |
| М0 |
| δ |
 или
или 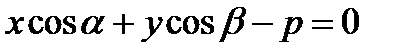 . (8)
. (8)
Если положение прямой относительно осей координат определять длиной р перпендикуляра, опущенного из начала координат на прямую и углом α, образуемым этим перпендикуляром с положительным направлением оси (Ох).
Общее уравнение прямой может быть приведено к нормальному уравнению путем домножения на нормирующий множитель 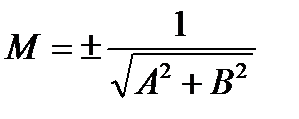 . Знак М выбирается противоположным к знаку С.
. Знак М выбирается противоположным к знаку С.
Отклонение точки М0(х0,у0) от прямой (а) вычисляется по формуле: 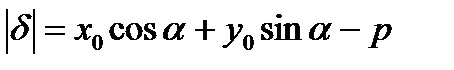 .
.
Расстояние от точки М0(х0,у0) до прямой 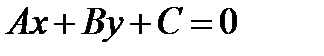
| М0 |
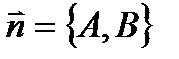 М0 М0
|
| d |
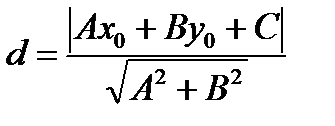 (9)
(9)
Пример 1. Дана прямая (а): 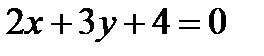 . 1) Составить уравнение прямой (а1), проходящей через точку М0 (2, 1), параллельно данной прямой. 2) Составить уравнение прямой (а2), проходящей через точку М0 (2, 1), перпендикулярно данной прямой.
. 1) Составить уравнение прямой (а1), проходящей через точку М0 (2, 1), параллельно данной прямой. 2) Составить уравнение прямой (а2), проходящей через точку М0 (2, 1), перпендикулярно данной прямой.
Решение.
1) 1 способ. Найдем угловой коэффициент прямой (а): 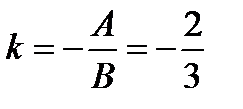 . Условие параллельности двух прямых:
. Условие параллельности двух прямых: 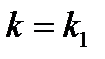 , то есть угловой коэффициент прямой (а1):
, то есть угловой коэффициент прямой (а1): 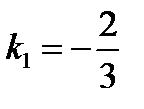 . Подставим в уравнение (3):
. Подставим в уравнение (3): 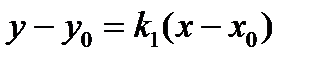 и получим
и получим  . Отсюда общее уравнение прямой (а1) имеет вид:
. Отсюда общее уравнение прямой (а1) имеет вид:
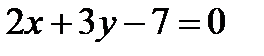 .
.
2 способ. Нормальный вектор 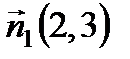 Прямые параллельны, следовательно, параллельны их нормальные вектора. То есть нормальный вектор прямой (а1):
Прямые параллельны, следовательно, параллельны их нормальные вектора. То есть нормальный вектор прямой (а1): 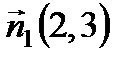 . Подставим в уравнение (2):
. Подставим в уравнение (2): 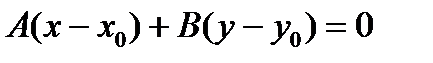 и получим
и получим 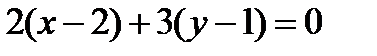 . Отсюда общее уравнение прямой (а1) имеет вид:
. Отсюда общее уравнение прямой (а1) имеет вид: 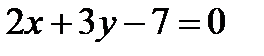 .
.
2) 1 способ. Найдем угловой коэффициент прямой (а): 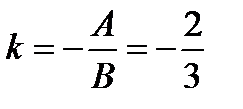 . Условие перпендикулярности двух прямых:
. Условие перпендикулярности двух прямых: 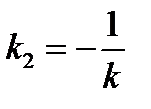 , то есть угловой коэффициент прямой (а2):
, то есть угловой коэффициент прямой (а2): 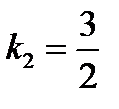 . Подставим в уравнение (3):
. Подставим в уравнение (3): 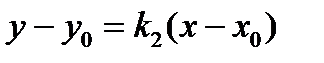 и получим
и получим  . Отсюда общее уравнение прямой (а1) имеет вид:
. Отсюда общее уравнение прямой (а1) имеет вид: 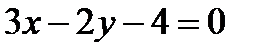 .
.
2 способ. Нормальный вектор 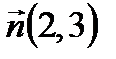 Прямые перпендикулярны, следовательно, нормальный вектор прямой (а) параллелен прямой (а2), то есть является направляющим вектором прямой (а2):
Прямые перпендикулярны, следовательно, нормальный вектор прямой (а) параллелен прямой (а2), то есть является направляющим вектором прямой (а2):  . Подставим в уравнение (4):
. Подставим в уравнение (4): 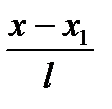
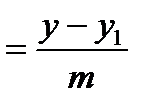 и получим
и получим 
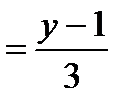 ,. Отсюда общее уравнение прямой (а2) имеет вид:
,. Отсюда общее уравнение прямой (а2) имеет вид: 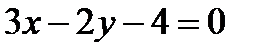 .
.
Пример 2. Найти расстояние от прямой (АВ), где А(7, 4), В(3, –3) до точки С(5, 9).
Решение. Найдем общее уравнение прямой. Для этого подставим исходные данные в формулу (4):  и получим
и получим 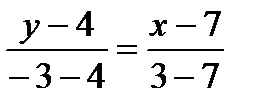 . Отсюда общее уравнение (АВ)
. Отсюда общее уравнение (АВ) 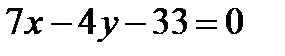 . По формуле (9)
. По формуле (9) 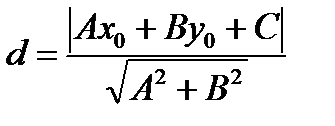 найдем искомое расстояние:
найдем искомое расстояние: 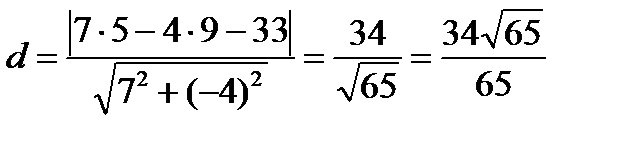 .
.
Дата: 2019-02-24, просмотров: 389.