| у |
| х |
| z |
| М1 |
| М2 |
| М |
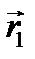
|
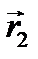
|

|
| О |
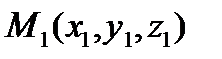 и
и  . Известно, что некая точка
. Известно, что некая точка 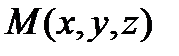 делит отрезок [М1М2] в отношении λ:
делит отрезок [М1М2] в отношении λ: 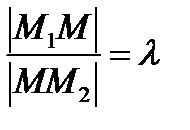 или, что тоже самое
или, что тоже самое 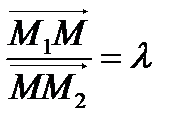 .
.
Найдем координаты точки М.
Обозначим 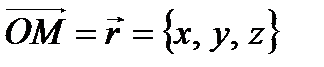 ,
,  ,
,
 .
.
Разложим векторы по базису векторов 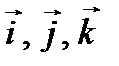 :
:
 ,
,  ,
, 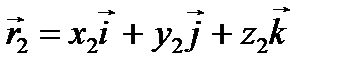 .
.
Имеем по правилу треугольника, что:
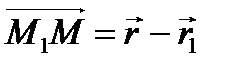 ,
, 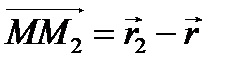 (*)
(*)
Из равенства 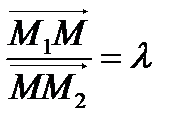 выразим вектор
выразим вектор 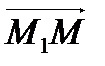 :
: 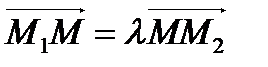 .
.
Подставим в данное равенство оба равенства (*). Имеем: 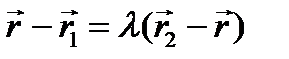 . Отсюда
. Отсюда 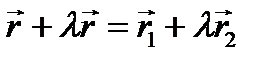 . Выразим вектор
. Выразим вектор  :
: 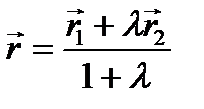 .
.
Приравнивая проекции обеих частей на x, y, z , получим:
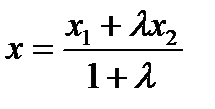 ,
, 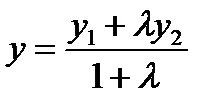 ,
,  - координаты точки М.
- координаты точки М.
Если точка М делит отрезок [М1М2] пополам, то есть λ = 1, то координаты точки М находятся по формулам: 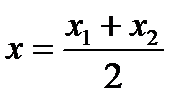 ,
, 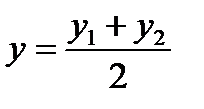 ,
,  .
.
Пример. Найти координаты точки М, которая делит отрезок [М1М2] , где  ,
, 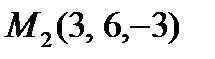 в отношении 2 к 3.
в отношении 2 к 3.
Решение.
Дано 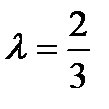 . Тогда
. Тогда 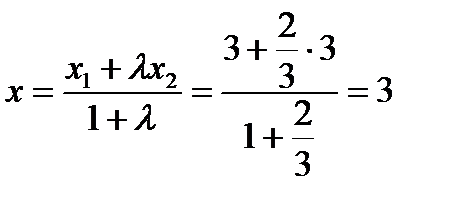 ,
, 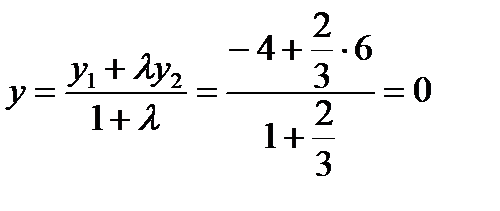 ,
, 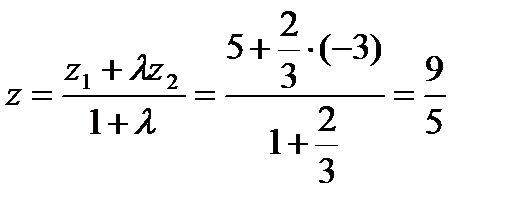 . Ответ:
. Ответ: 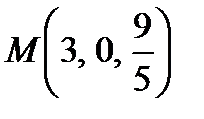 .
.
Скалярное произведение векторов
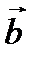
|
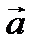
|
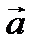 и
и 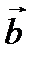 называется число, равное произведению модулей этих векторов на косинус угла между ними
называется число, равное произведению модулей этих векторов на косинус угла между ними
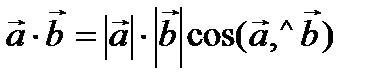 =
= 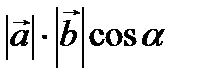 . (1)
. (1)
Скалярное произведение – это число (скаляр).
Скалярное произведение более, чем двух векторов не рассматривается.
Из формулы (1) следует, что
 (2)
(2)
Проекции вектора на вектор
Известно, что проекция вектора на ось l вычисляется по формуле Пр l  =
= 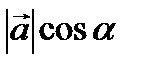 , где
, где 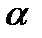 - угол между вектором и осью. Пусть вектор
- угол между вектором и осью. Пусть вектор 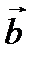 лежит на оси l и сонаправлен с ней. Тогда
лежит на оси l и сонаправлен с ней. Тогда 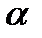 - угол между векторами
- угол между векторами 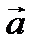 и
и 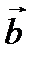 . Проекция вектора
. Проекция вектора 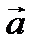 на вектор
на вектор 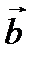 вычисляется по формуле: Пр
вычисляется по формуле: Пр 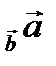 =
= 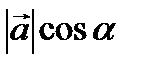 .
.
Домножим обе части равенства на  , получим:
, получим:
 Пр
Пр 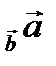 =
= 
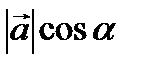 , тогда, по определению,
, тогда, по определению,  Пр
Пр 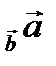 =
= 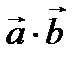 . Отсюда,
. Отсюда,
Пр 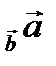 =
= 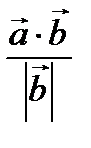 или Пр
или Пр 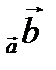 =
= 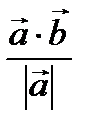 . (3)
. (3)
Геометрический смысл скалярного произведения
Скалярное произведение вектора 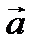 на единичный вектор
на единичный вектор 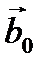 равно проекции вектора
равно проекции вектора 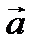 на направление, определяемой вектором
на направление, определяемой вектором 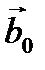 , то есть
, то есть  = Пр
= Пр 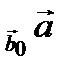 .
.
Механический смысл скалярного произведения
Скалярное произведение силы 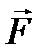 на вектор
на вектор 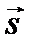 равно работе А этой силы при перемещении материальной точки по вектору
равно работе А этой силы при перемещении материальной точки по вектору 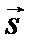 :
: 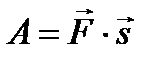 . (4)
. (4)
Свойства скалярного произведения
1. 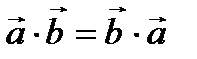
2. Скалярный квадрат равен квадрату модуля: 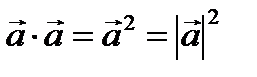
Доказательство: 
3. Если  – действительное число, то
– действительное число, то 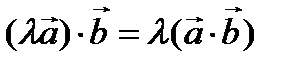
4. 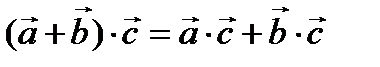
5.  (5)
(5)
Доказательство.
Доказательство необходимости: 1) Пусть 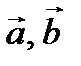 – ненулевые векторы. Тогда скалярное произведение
– ненулевые векторы. Тогда скалярное произведение 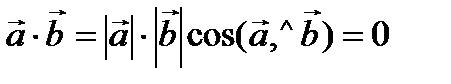 тогда и только тогда, когда
тогда и только тогда, когда 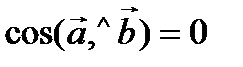 , т.е. когда
, т.е. когда 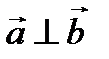 . 2) Пусть среди векторов
. 2) Пусть среди векторов 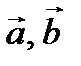 может быть нулевой вектор (или оба нулевые). По определению
может быть нулевой вектор (или оба нулевые). По определению 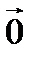 -вектор можно считать перпендикулярным любому вектору, т.е. пусть
-вектор можно считать перпендикулярным любому вектору, т.е. пусть 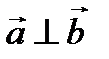 .
.
Доказательство достаточности: 1) Пусть 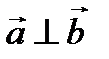 , причем
, причем 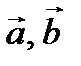 – ненулевые векторы. Тогда скалярное произведение
– ненулевые векторы. Тогда скалярное произведение  , так как
, так как  . 2) Пусть
. 2) Пусть 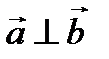 , причем среди векторов
, причем среди векторов 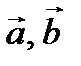 может быть нулевой вектор (или оба нулевые). Тогда скалярное произведение
может быть нулевой вектор (или оба нулевые). Тогда скалярное произведение 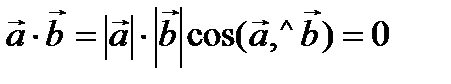 , так как длина нулевого вектора равна 0. (что и треб. док.).
, так как длина нулевого вектора равна 0. (что и треб. док.).
6. Если  , то угол между
, то угол между 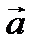 и
и 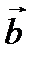 – острый, если
– острый, если 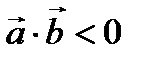 , то угол между
, то угол между 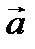 и
и 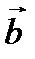 – тупой. И наоборот.
– тупой. И наоборот.
Таблица скалярного умножения ортов

|
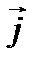
|
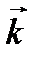
|
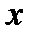
|
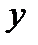
|
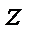
|
| 1 |
| 1 |
| 1 |
| O |
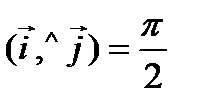 ,
, 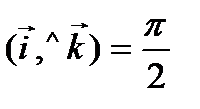 ,
, 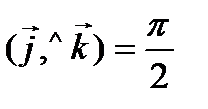 ,
, 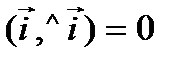 ,
, 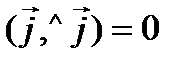 ,
,
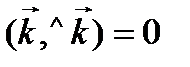 ; тогда
; тогда 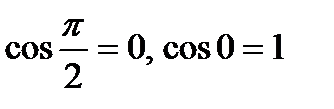 ; длины ортов равны
; длины ортов равны 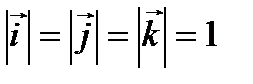 .
.
Следовательно, исходя из определения скалярного произведения, можем записать, что
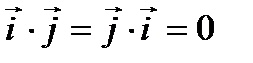 ,
, 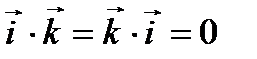 ,
, 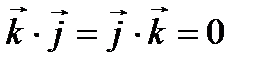 ,
, 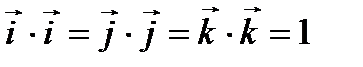 .
.
Дата: 2019-02-24, просмотров: 387.