Полярная система координат (ПСК) на плоскости определяется заданием некоторой точки О – полюса, луча (ОР) – полярной оси и единицы масштаба.
Положение любой точки М в ПСК характеризуется координатами ρ и φ и, наоборот, каждому набору координат отвечает точка.
| Р |
| 1 |
| M(ρ, φ) |
| О |
| φ |
| ρ |
φ – полярный угол – угол, откладываемый от полярной оси против часовой стрелки до луча (ОМ), причем 0 ≤ φ ≤ 2π.
| Р |
| 1 |
| M |
| О |
| φ |
| х |
| х |
| у |
| у |
| ρ |
Совместим системы координат так, чтобы ось (Ох) совпадала с полярной осью (ОР), а начало координат совпадало с полюсом.
Декартовые координаты точки М – х, у. Полярные координаты этой же точки – ρ, φ.
Из прямоугольного треугольника следует:
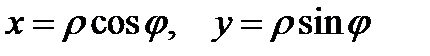 (1)
(1) 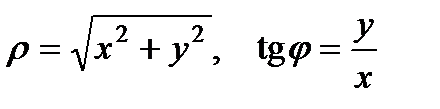 (2)
(2)
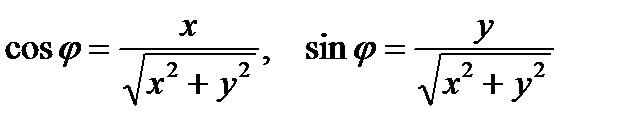 (3)
(3)
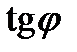 определяет два угла: φ и φ + π, формулы (3) уточняют, какой из них рассматривать.
определяет два угла: φ и φ + π, формулы (3) уточняют, какой из них рассматривать.
Определение. Уравнение Ф(ρ,φ) = 0 определяет на плоскости некоторую линию l, представляющую собой геометрическое место точек, координаты которых удовлетворяют данному уравнению. И наоборот.
Обычно уравнение разрешено относительно переменной ρ: ρ = f(φ).
Чтобы перейти от уравнения линии в декартовой системе координат F(x, y) = 0 к ее полярному уравнению Ф(ρ,φ) = 0 нужно подставить вместо х и у формулы (1). Обратный переход от Ф(ρ, φ) = 0 к F(x, y) = 0 получается с помощью формул (2) и (3).
Пример 1. Найти полярное уравнение прямой х = 1.
Решение. х = 1 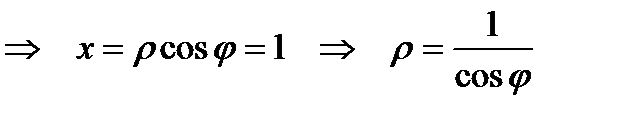 – уравнение прямой.
– уравнение прямой.
Пример 2. Найти декартовое уравнение кривой 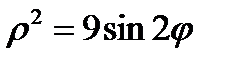 .
.
Решение. Используем формулы (2) и (3): 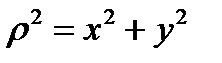 ,
, 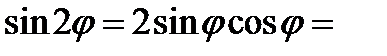
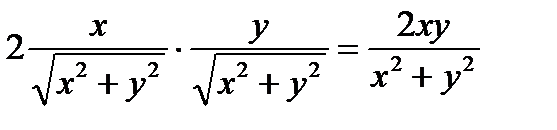 . Подставим в уравнение:
. Подставим в уравнение: 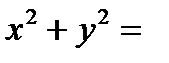
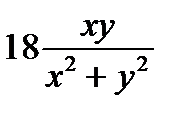 , отсюда
, отсюда 
 .
.
П. 3. Параметрическое задание линий в ДСК и ПСК.
Иногда обе координаты х, у или ρ, φ оказываются заданными как функции некоторой третьей переменной t, являющейся параметром, определяющей положение точки на плоскости (когда t меняется, точка перемещается, описывая некоторую линию).
Параметрическое уравнение линии в ДСК:  или
или 
Параметрическое уравнение линии в ПСК: 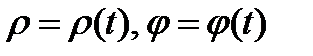 или
или 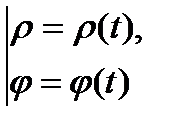
Чтобы перейти к уравнению линии в общей форме F(x,y) = 0 или Ф(ρ,φ) = 0 надо из двух параметрических уравнений исключить параметр t, например, в ДСК в первом уравнении выразить параметр t через х и подставить во второе уравнение. Но это не всегда целесообразно.
Графики строят путем задания х (ρ), получая значения параметра t, затем с помощью известного t, получая значение у(φ).
Пример. Составить параметрические уравнения кривой 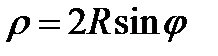 в ПСК и ДСК.
в ПСК и ДСК.
Решение. Пусть полярный угол φ будет параметром t
1) ПСК. Параметрическое уравнение кривой имеет вид: 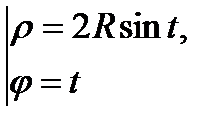 , где
, где 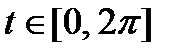 , так как
, так как 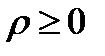 .
.
2) ДСК. 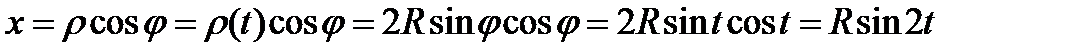 .
.
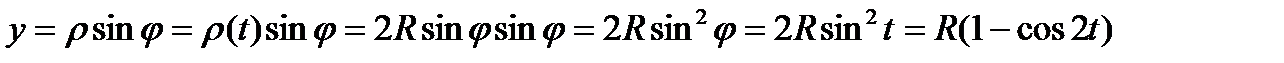 .
.
Тогда параметрическое уравнение кривой имеет вид: 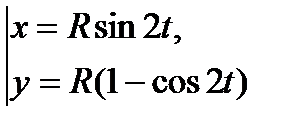
Дата: 2019-02-24, просмотров: 375.