Задача 1. Дана плоскость 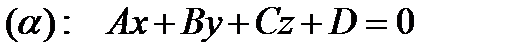 с нормальным вектором
с нормальным вектором 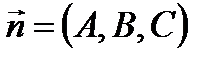 и прямая
и прямая 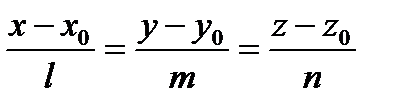 с направляющим вектором
с направляющим вектором  , которая пересекает плоскость в некоторой точке Е.
, которая пересекает плоскость в некоторой точке Е.
Найти угол между прямой и плоскостью.
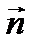
|
| а |

|
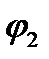
|
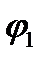
|
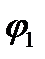 – угол между прямой и плоскостью.
– угол между прямой и плоскостью. 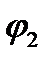 – угол между
– угол между 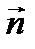 и
и 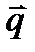 .
.
| α |
 ,
,  , отсюда
, отсюда
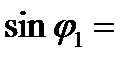
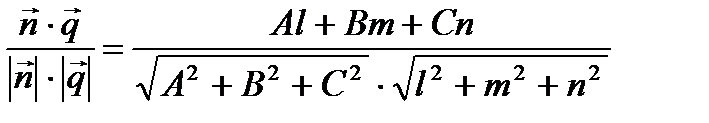 (1)
(1)
Задача 2. Дана плоскость 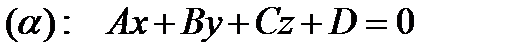 с нормальным вектором
с нормальным вектором 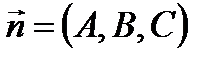 и точка
и точка 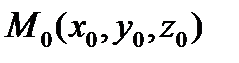 , не принадлежащая плоскости.
, не принадлежащая плоскости.
| α |
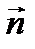 α α
|
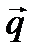 α α
|
| (а) |
| d |
| М0 |
| Е |
Решение.
Проведем прямую (а) с направляющим вектором 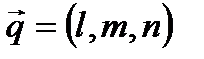 , проходящую через точку М0 перпендикулярно к плоскости (α). Ее уравнение:
, проходящую через точку М0 перпендикулярно к плоскости (α). Ее уравнение: 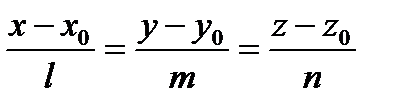 . Так как (а)
. Так как (а) 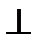 (α), то верно, что
(α), то верно, что 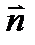
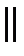
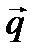 . Тогда можем записать, что
. Тогда можем записать, что 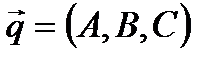 и уравнение прямой примет вид:
и уравнение прямой примет вид:  или в параметрическом виде
или в параметрическом виде 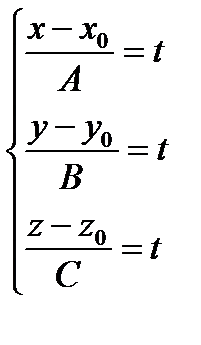 .
.
Пусть прямая и плоскость пересекаются в точке Е. Тогда 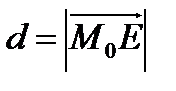 .
.
Найдем координаты точки Е. Так как это точка пересечения прямой и плоскости, то ее координаты – решение системы 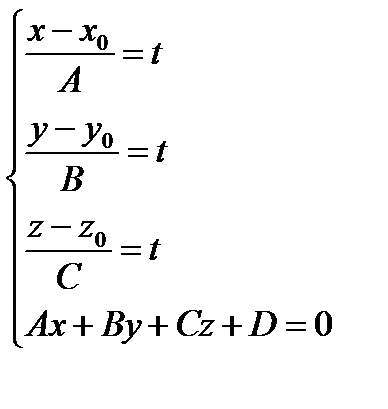 . Перепишем ее в виде
. Перепишем ее в виде  .
.
Подставим выражения для x, y, z в 4-ое уравнение системы, получим:
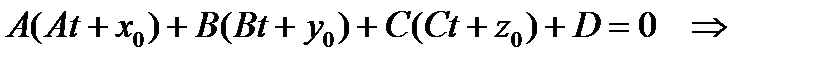
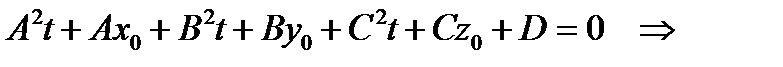
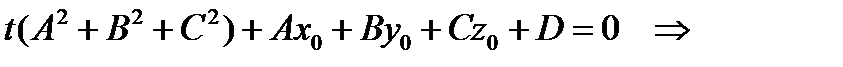
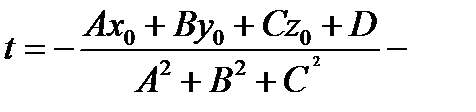 число, пусть t = t0.
число, пусть t = t0.
Подставим известное t0 в выражения для x, y, z, т.е. в первые три уравнения системы:
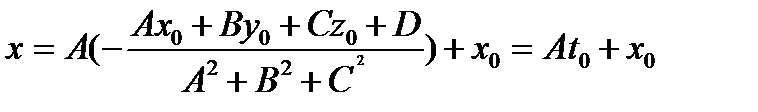 ,
,
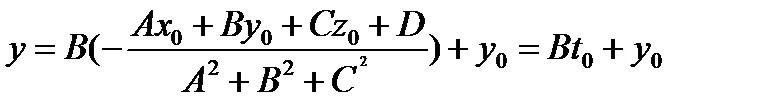 ,
,
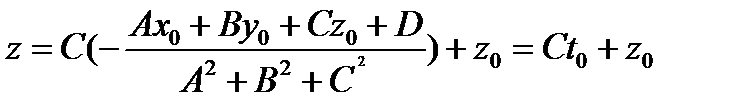 .
.
Следовательно, координаты точки Е: 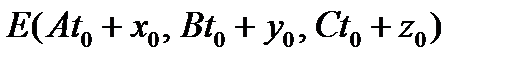 . Тогда координаты вектора
. Тогда координаты вектора 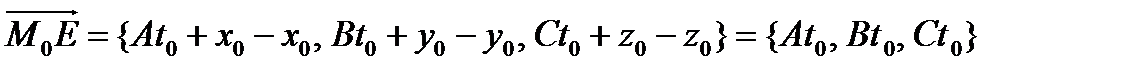 . Найдем
. Найдем 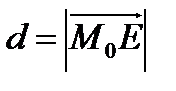 .
.
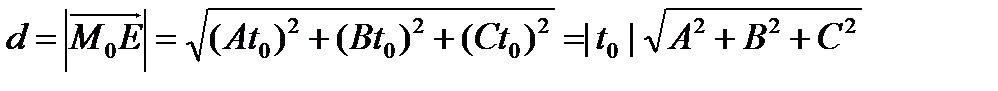 = (подставим вместо t0 его значение) =
= (подставим вместо t0 его значение) = 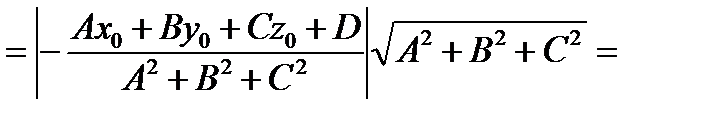
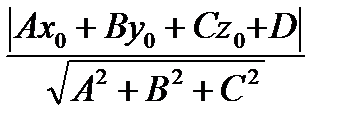 .
.
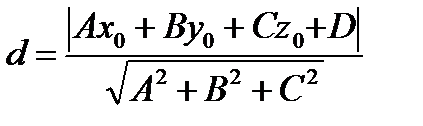 – расстояние от точки
– расстояние от точки 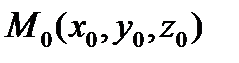 до плоскости
до плоскости 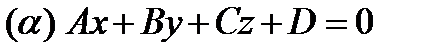 (2)
(2)
Примеры.
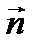 α α
|
| М0 |
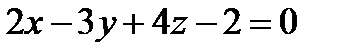 , проходящей через точку М0(0, 0, 1/2).
, проходящей через точку М0(0, 0, 1/2).
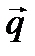
|
| α |
Нормальный вектор плоскости коллинеарен направляющему вектору
прямой 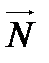
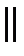
 . Следовательно, координаты направляющего
. Следовательно, координаты направляющего
вектора прямой пропорциональны (совпадают) с координатами нормального вектора.
Подставим данные в каноническое уравнение: Ответ: 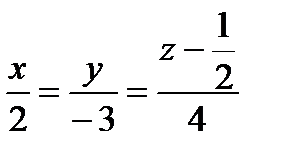
Задача 2. Найти точку пересечения прямой  и плоскости
и плоскости 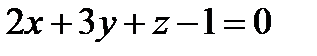 .
.
Решение.
Координаты точки пересечения М – это решение системы 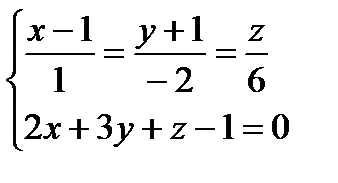 .
.
| α |
| М |
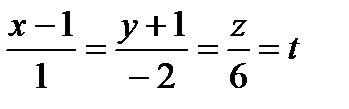 , отсюда
, отсюда 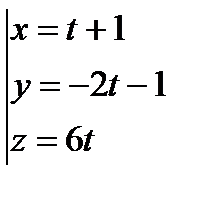 .
.
Найдем решение системы:
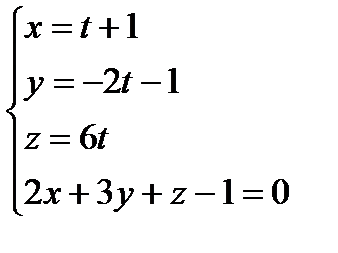
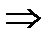
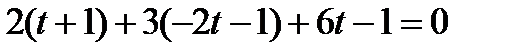
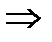
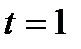 ,
,
отсюда х = 1+1=2, у = -2 - 1= -3, z = 6 – координаты точки пересечения. Ответ: 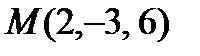 .
.
Задача 3. Найти угол 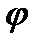 между прямой в:
между прямой в: 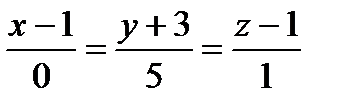 и плоскостью
и плоскостью  :
: 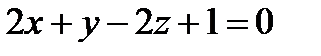 .
.
Решение.
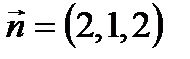 ,
,  . Угол между прямой и плоскостью находится по формуле:
. Угол между прямой и плоскостью находится по формуле:
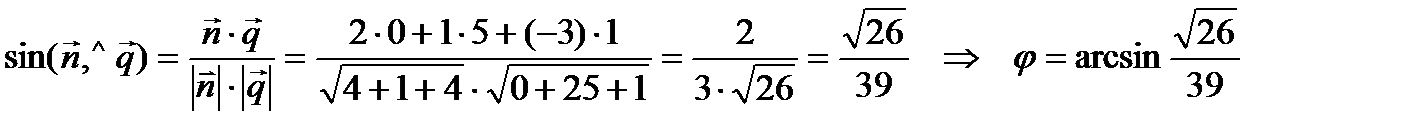 .
.
Задача 4. Написать уравнение проекции прямой l: 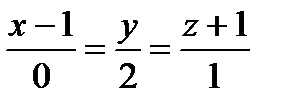 на плоскость
на плоскость  :
: 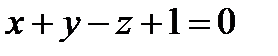 .
.
Решение.
 α α
|

|
 ,
, 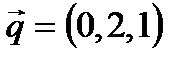 .
.
| α1 |
| А |
 ,
,
| l |
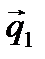 А А
|
 .
. | α |
| d |
Пересечение полученной плоскости с плоскостью  -
-
прямая d - и будет искомой проекцией.
Уравнение плоскости 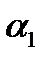 , походящей через прямую l перпендикулярно плоскости
, походящей через прямую l перпендикулярно плоскости  можно найти либо 1 методом, либо 2-ым. Это уравнение имеет вид:
можно найти либо 1 методом, либо 2-ым. Это уравнение имеет вид:  . Нормальный вектор
. Нормальный вектор 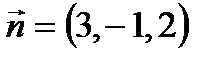 .
.
Тогда общее уравнение искомой прямой d имеет вид: 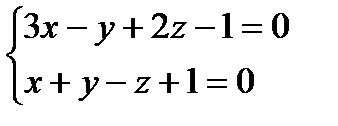 .
.
Запишем это уравнение в каноническом виде. Для этого необходимо найти точку А, лежащую на прямой, и направляющий вектор 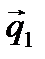 .
.
Найдем координаты точки А: пусть z = 0, тогда 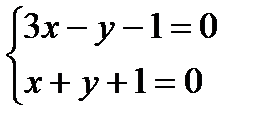 , методом Гаусса получим, что
, методом Гаусса получим, что
х = 0, у =-1. Координаты точки А(0, -1, 0).
Направляющий вектор  найдем по формуле:
найдем по формуле: 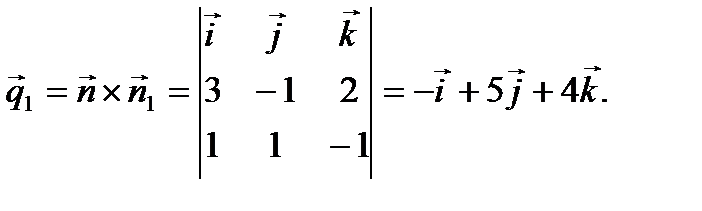
Уравнение прямой d – уравнение искомой проекции имеет вид: 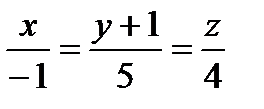 .
.
Дата: 2019-02-24, просмотров: 351.