Для того чтобы система m линейных уравнений с n неизвестными была совместной, необходимо и достаточно, чтобы ранг матрицы системы был равен рангу расширенной матрицы. При этом

1) если 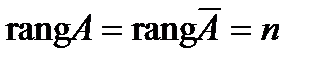, то система имеет единственное решение,

2) если 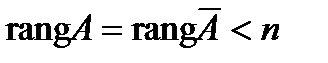, то система имеет бесконечное множество решений.

Пример 1. Определить, сколько решений имеет система .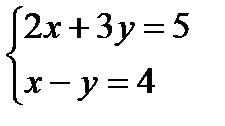

Решение.  Найдем ранги матрицы системы и расширенной матрицы системы.

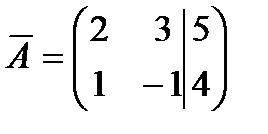
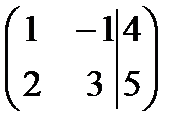
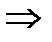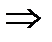
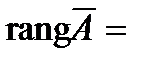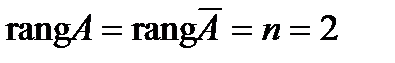   две ненулевые строки 2. Если закрыть столбец свободных членов, то получим матрицу системы, которая так же имеет две ненулевые строки, следовательно,   Число неизвестных – два: x, y. Получили, что , следовательно, система имеет единственное решение.

Пример 2. Определить, сколько решений имеет система уравнений .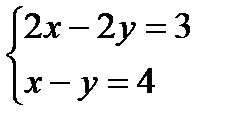

Решение.  Найдем ранги матрицы системы и расширенной матрицы системы.

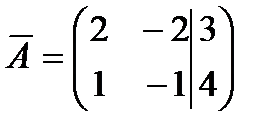
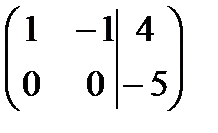
   две ненулевые строки 2. Если закрыть столбец свободных членов, то получим матрицу системы, которая имеет одну ненулевую строку, следовательно, 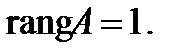  Получили, что 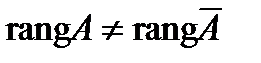, следовательно, система не имеет решений.

П. 2. Методы решения систем линейных уравнений.

Пп. 1. Метод Гаусса

 (для решения однородных и неоднородных систем, когда )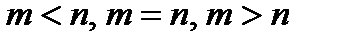

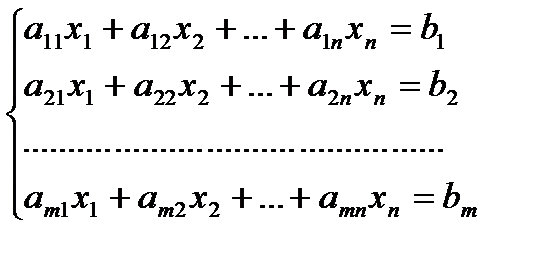- неоднородная, 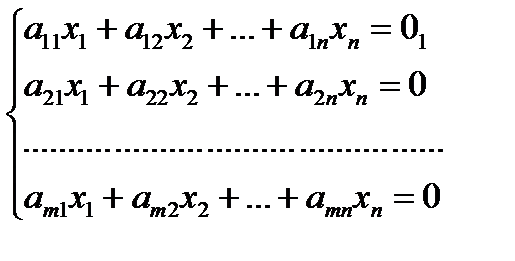- однородная.

Метод заключается в последовательном исключении неизвестных, с помощью элементарных преобразований над строками расширенная матрица системы приводится к трапециевидной или к треугольной форме, при этом удобнее, чтобы все ведущие элементы были равны 1 (алгоритм нахождения рангов), либо устанавливается, что система несовместна. Это прямой ход метода Гаусса.

Прямой ход метода Гаусса:

1. Записываем расширенную матрицу системы .

2. Переставляя строки, добиваемся, чтобы 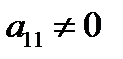; удобнее, чтобы  и, если в первом столбце есть 1, то именно эту строку делаем первой. Первую строку назовем рабочей, элемент 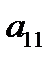- ведущим.

3. Ведущий элемент рабочей строки должен быть равен 1. Если 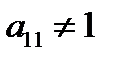, то делим первую строку на .

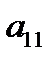    4. Умножая первую строку на числа 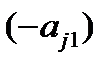, где 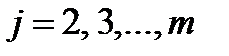, и прибавляя ее соответственно ко второй и т.д. m-ой строке, получим в 1-ом столбце под 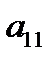нули.                                                                          5. Не трогая первой строки, путем перестановки остальных строк, добиваемся, чтобы 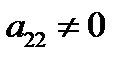, а лучше, если во втором столбце, кроме первой строки, есть 1, чтобы 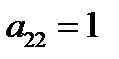, (рабочей стала вторая строка, ведущим – элемент ).

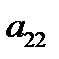6. Если 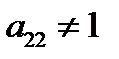, то делим вторую строку на 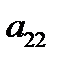, получим ведущий элемент равным 1.

7. Умножая вторую строку на числа 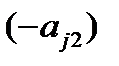, где 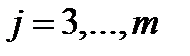, и прибавляя ее соответственно к третьей и т.д. m-ой строке, получим во 2-ом столбце под  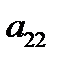нули.

8. И так далее, пока расширенная матрица системы не приведется к трапециевидной форме. На главной диагонали полученной матрицы стоят единицы.

Например, .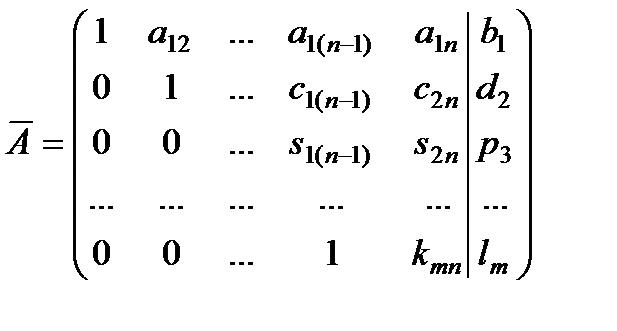

9. Находим ранги матрицы-системы и расширенной матрицы системы. Проверяем условия теоремы Кронекера-Капелли. Делаем вывод о количестве решений системы: одно решение, либо бесконечное множество решений, или нет решений.

Обратный ход заключается в последовательном нахождении неизвестных. Для этого полученная трапециевидная или треугольная матрица записывается снова в виде системы уравнений, и из нее алгебраическим путем, начиная с последнего уравнения, находятся неизвестные.

В нашем примере получаем бесконечное множество решений, которые находятся из системы:

.

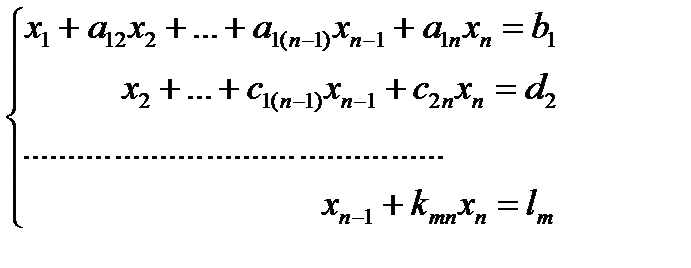В случае бесконечного множества решений все переменные делятся на базисные и свободные.

Определение 21. Базисным минором называется ненулевой минор максимального порядка основной матрицы, находящийся в левом верхнем углу. Базисные переменные – это переменные, коэффициенты при которых образуют базисный минор. Остальные переменные называются свободными, т.е. это переменные, которым можно придавать произвольные действительные значения.

Количество базисных переменных равно .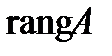

Количество свободных переменных можно найти с помощью формулы: .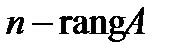

Все получившиеся базисные переменные (в примере 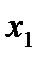, , 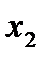…, 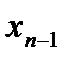) выражаются через свободные (в примере 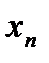) и находится решение системы, либо, если все переменные являются базисными, то выражается в численном виде единственное решение системы линейных уравнений.

Эта процедура начинается с последнего уравнения, из которого выражают соответствующую базисную переменную (а она там всего одна) и подставляют в предыдущие уравнения, и так далее, поднимаясь по «ступенькам» наверх. Каждой строчке соответствует ровно одна базисная переменная, поэтому на каждом шаге, кроме последнего (самого верхнего), ситуация в точности повторяет случай последней строки.

В примере: , …, , .

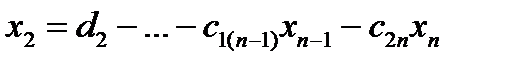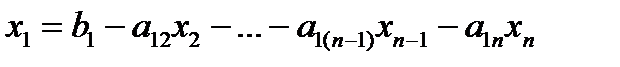Ответ примера: {( , … , ), }.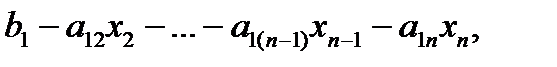

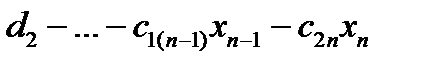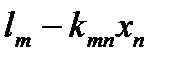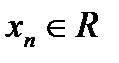Определение 22. Базисным решением называется частное решение, получающееся из общего при нулевых значениях свободных переменных.