Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

1. Определитель квадратной матрицы порядка n = 1:

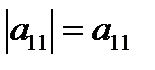Пример.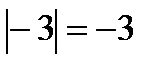

2.Определитель квадратной матрицы порядка n = 2:

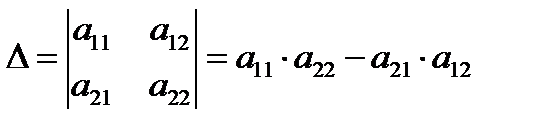
Пример. .

3. Определитель квадратной матрицы порядка n = 3:

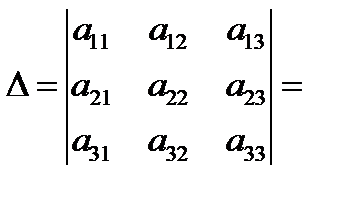
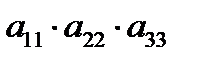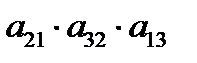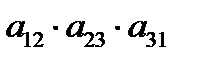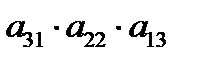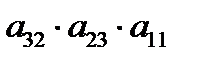+ + – – – – правило треугольников.

Пример.

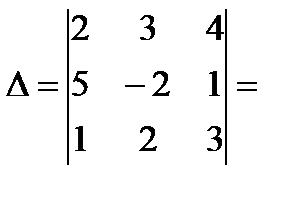
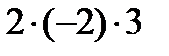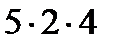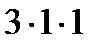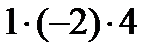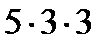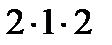+ + – – – = – 10.

4. Определитель квадратной матрицы порядка n вычисляется либо методом понижения порядка, либо методом приведения к треугольному виду.

Рассмотрим вычисление определителя методом понижения порядка. Прежде, чем его рассмотреть, отметим ряд свойств определителя и дадим несколько определений.

Свойства определителя

1. Определитель не изменяется при транспонировании.

2. При перестановке двух строк (столбцов) определитель меняет знак.

3. Если две строки (столбца) определителя совпадают, то он равен нулю.

4. Если все элементы какой-нибудь строки (столбца) определителя имеют общий множитель, то его можно вынести за знак определителя.

5. Если все элементы какой-нибудь строки (столбца) определителя есть нули, то det А = 0.

6. Если элементы двух строк (столбцов) взаимно пропорциональны, то det А = 0.

7. Если каждый элемент некоторой строки определителя представляет собой сумму двух слагаемых, то определитель представляется в виде суммы двух определителей, у которых элементы рассматриваемой строки в первом определителе равны первым слагаемым, во втором – вторым. (Аналогично со столбцами). Например,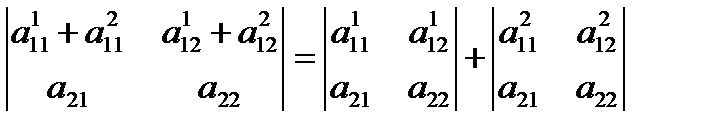

8. Определитель не изменится, если к элементам одной строки (столбца) прибавить другую строку (столбец), умноженную на действительное число.

9. Определитель треугольной матрицы равен произведению элементов, стоящих на ее главной диагонали.

 

Определение 14. Минором 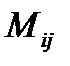определителя, соответствующим элементу  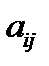называется определитель, получаемый из данного вычеркиванием строки и столбца, на пересечении которых стоит данный элемент. 

Определение 15. Алгебраическим дополнением элемента 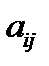 называется число, вычисляемое по формуле .   

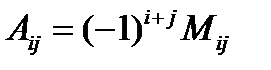Пример. Найти 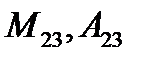, А₁₃,  .

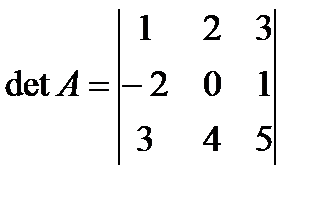Решение.

Вычеркнем в определителе вторую строку и третий столбец, тогда минор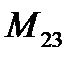

. . .

 

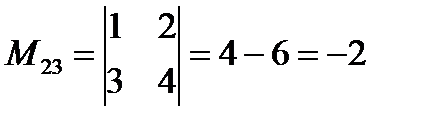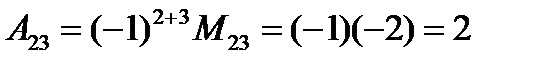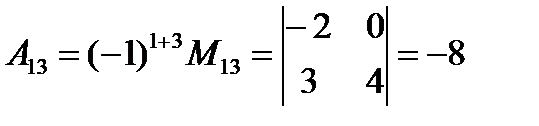Метод понижения порядка.

 

Определитель равен сумме произведений элементов какой-либо строки или столбца на их алгебраические дополнения:

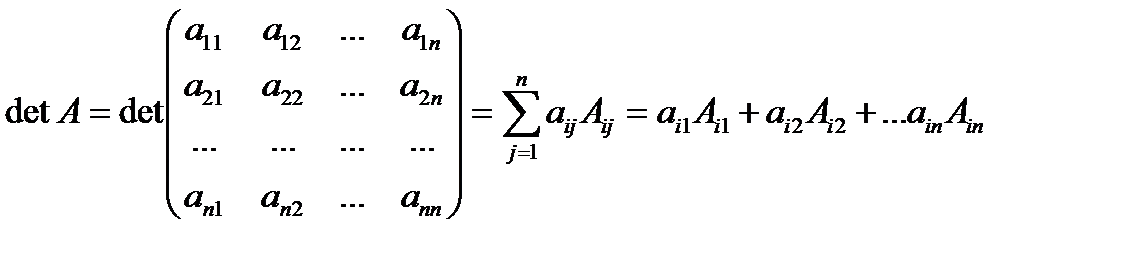 - разложение определителя по i-той строке.

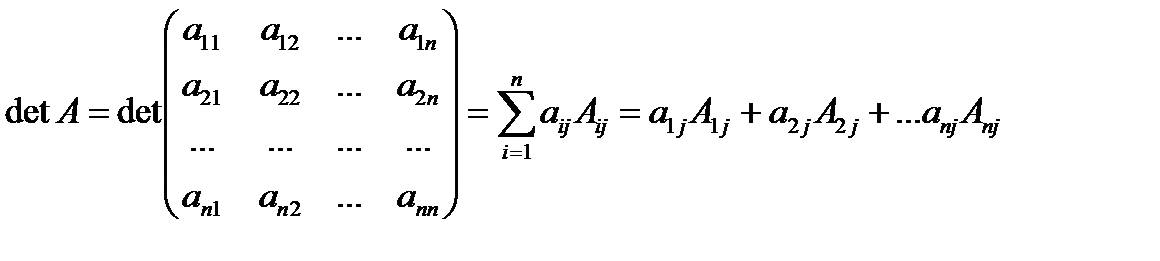 - разложение определителя по j-тому столбцу.

 

Пример. Вычислить определитель путем разложения по 1-ой строке и второму столбцу.

Решение.

По первой строке: .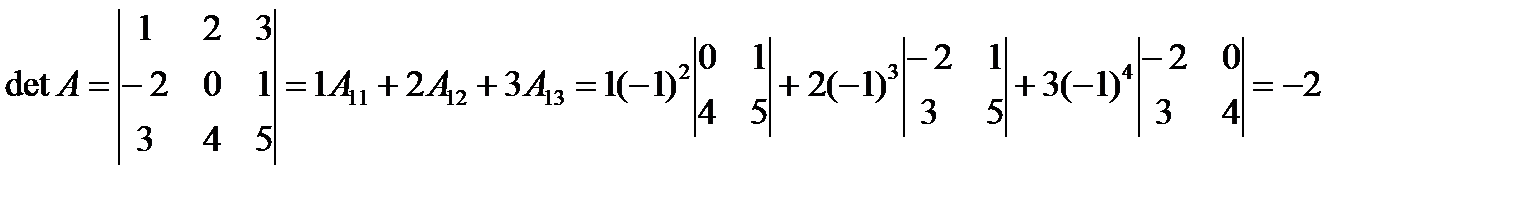

 

По второму столбцу: .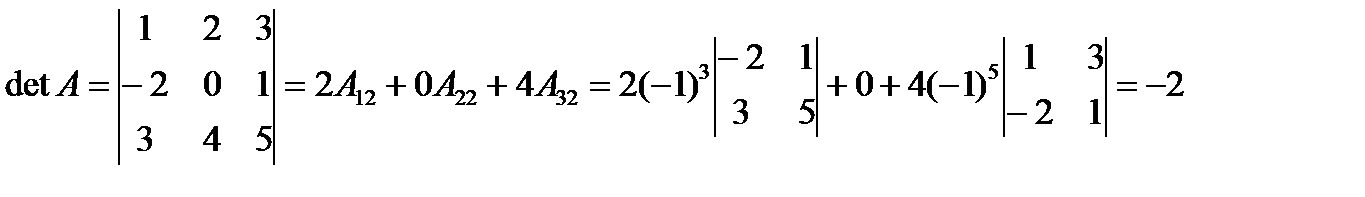

Определение 16. Матрица называется невырожденной, если ее определитель не равен нулю и вырожденной в противном случае.

Замечание (об обратной матрице). В алгебре матриц нет понятия деления матриц. Для невырожденных матриц существует обратная матрица.

Определение. Матрица 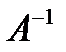 называется обратной к матрице А, если  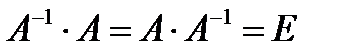, где Е – единичная матрица.

Теорема о вычислении обратной матрицы. Если А невырожденная ( 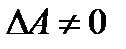) матрица порядка n, то обратная к ней матрица находится по формул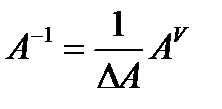е , где 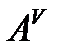– присоединенная матрица, то есть транспонированная матрица, составленная из алгебраических дополнений.

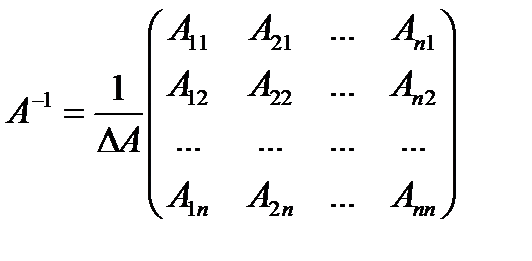
Понятие о ранге матрицы.

Определение 17. Строки матрицы А называются линейно зависимыми, если какая-либо из них линейно выражается через остальные. В противном случае – строки линейно независимы. (аналогично столбцы).

Пример. 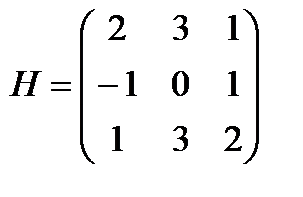. Найти количество линейно независимых строк и столбцов.

Решение. Обозначим строки: Е₁ = (2 3 1), Е₂ = (–1 0 1), Е₃ = (1 3 2). Видно, что Е₃ = Е₁ + Е₂, следовательно, Е₁, Е₂, Е₃ – линейно зависимы. Е₂ ≠ k Е₁, следовательно, Е₁ , Е₂ – линейно независимы. Вывод: матрица имеет две линейно независимых строки.

Обозначим столбцы: F₁, F₂, F₃. Видно, что F₂ = F₁ + F₃, следовательно, F₁, F₂, F₃ – линейно зависимы. F₁ ≠ k F₂, следовательно, F₁, F₂ – линейно независимы. Вывод: матрица имеет два линейно независимых столбца.

 

Можно доказать, что для любой матрицы максимальное число линейно независимых строк и максимальное число линейно независимых столбцов совпадают.

Определение 18. Ранг матрицы равен максимально возможному числу ее линейно независимых строк (столбцов).

Т.е. в примере rang H = 2.

 

Замечание. Ранг квадратной матрицы не превосходит ее порядок. Ранг равен порядку в том и только в том случае, если матрица невырожденная. Ранг матрицы размера 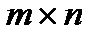 не превосходит меньшего из чисел m и n.

Не изменяют ранга элементарные преобразования над матрицами:

1. перестановка строк (столбцов),

2. умножение строки (столбца) на число, не равное нулю,

3. прибавление к строке (столбцу) другой строки (столбца), умноженной на число,

4. отбрасывание нулевых строк (столбцов),

5. транспонирование.

 

Если удастся путем элементарных преобразований привести матрицу к трапециевидной форме, то ееранг будет равен числу ее ненулевых строк!

 

При приведении матрицы к трапециевидной форме удобно пользоваться численным методом Гаусса:

 1) переставляя строки, добиваемся, чтобы 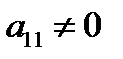 и 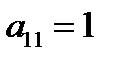, последнее можно достичь (если в первом столбце нет единиц) путем деления всей строки на . Первую строку называют рабочей, а элемент – ведущим.

2) умножаем первую строку на числа ( 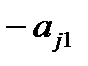), где 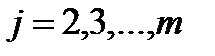, прибавляем ее соответственно ко второй и т.д. m-ой строке, получаем в 1-ом столбце под  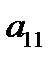 нули.

3) не трогая первой строки, добиваемся, чтобы 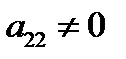 и 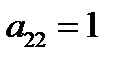 путем деления всей строки на или путем перестановки строк. Теперь вторая строка стала рабочей, а элемент 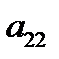– ведущим.

4) умножаем вторую строку на числа ( 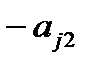), где 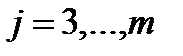, прибавляем ее соответственно к третей и т.д. m-ой строке, получаем во 2-ом столбце под   нули.

5) и т.д.

Пример. Найти ранг матрицы 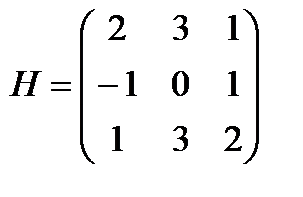.                                                                      Решение.  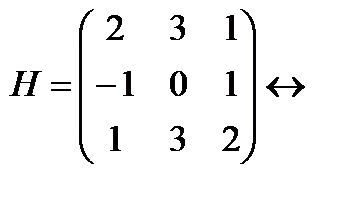(меняем строки местами)  (первую строку прибавляем ко второй) 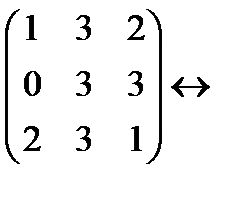(первую строку умножаем на (-2) и прибавляем к третьей)  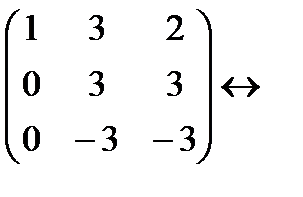(прибавляем ко второй строке третью) ,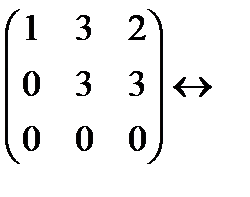

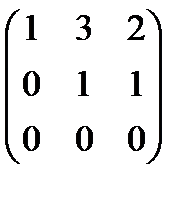Две ненулевые строки, то есть rang H = 2.

Системы линейных уравнений.

П. 1. Основные понятия.

 

Определение 19. Система уравнений вида 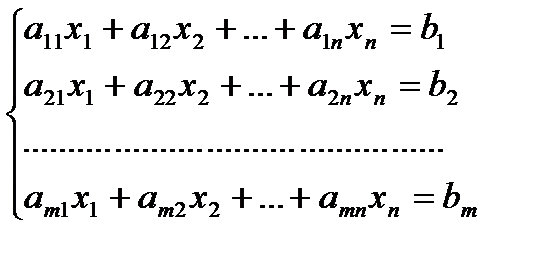 называется системой m линейных уравнений с n неизвестными , , …, .

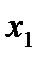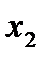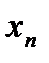Если все b_i = 0 ( i = 1, 2, 3,…, m), то система называется однородной, в противном случае неоднородной.

Матрица, состоящая из коэффициентов при неизвестных, называется матрицей системы. Матрица, состоящая из коэффициентов при неизвестных и столбца свободных членов, называется расширенной матрицей системы.

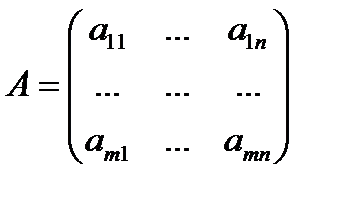 – матрица системы, 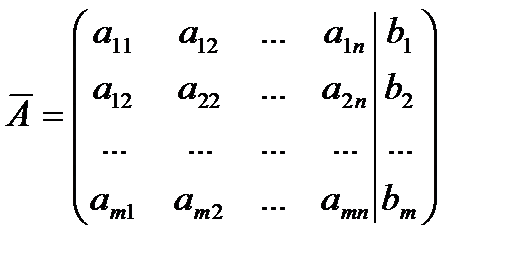– расширенная матрица системы,

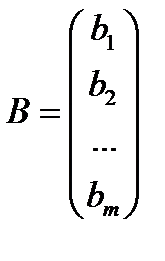– столбец свободных членов,  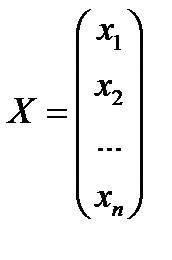– столбец неизвестных.

Матричная запись системы линейных уравнений имеет вид: .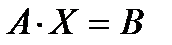

 

Определение 20. Система уравнений, имеющая хотя бы одно решение, называется совместной. Система, не имеющая решений, несовместной.

Элементарные преобразования системы (только над строками):

1. перестановка уравнений,

2. умножение уравнения на число, отличное от нуля,

3. прибавление к уравнению другого уравнения, умноженного на число.

Выполняют элементарные преобразования над расширенной матрицей системы и лишь над строками, так как перестановка столбцов соответствует переобозначению неизвестных.