Матрицы
П. 1. Основные определения
Определение 1. Матрица – прямоугольная таблица, состоящая из каких-либо объектов.
Впервые появились в середине IX века в работах английских математиков У. Гамильтона и А. Кэли.
Определение 2. Числовой матрицей размерности m  n называется таблица из (
n называется таблица из (  ) чисел, имеющая m строк и n столбцов
) чисел, имеющая m строк и n столбцов 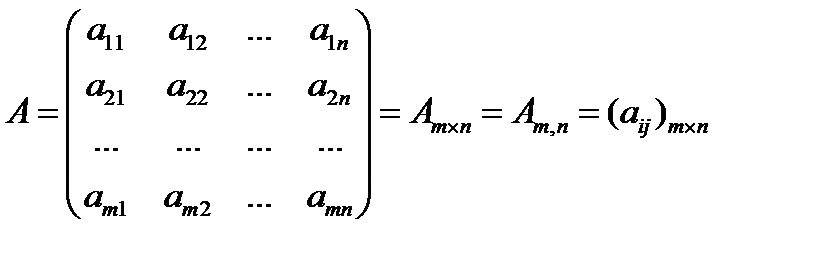 .
.
Обозначают матрицы большими буквами.
Числа, из которых составлена матрица, называются ее элементами: aij, где i – номер строки, j – номер столбца, на пересечении которых стоит элемент aij.
Например, матрица размерности 3 на 4 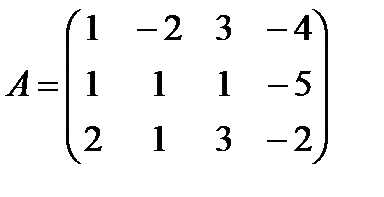 ,
, 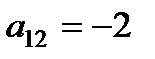 ,
,  ,
, 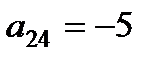 .
.
Определение 3. Матрица называется квадратной порядка n, если m = n, и прямоугольной размерности m на n, если m 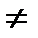 n.
n.
В примере выше матрица А – прямоугольная.
Элементы 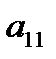 ,
,  , …,
, …, 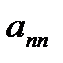 образуют главную диагональ матрицы, элементы
образуют главную диагональ матрицы, элементы 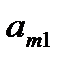 ,
,  , …,
, …, 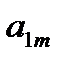 –побочную диагональ матрицы.
–побочную диагональ матрицы.
Например, у матрицы А главной диагональю является 1, 1, 3, побочной – 2, 1, 3.
Определение 4. Две матрицы называются равными, если их соответствующие элементы равны.
 , если aij = bij.
, если aij = bij.
Определение 5. Транспонированной матрицей (или сопряженной) к матрице  называется матрица
называется матрица 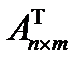 размерности n
размерности n  m, которая получается из матрицы А путем замены строк столбцами.
m, которая получается из матрицы А путем замены строк столбцами.
Например,  ,
, 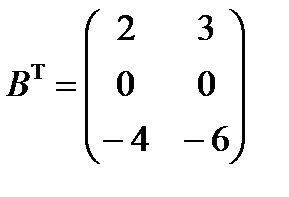 .
.
Определение 6. Квадратная матрица, у которой все элементы, не стоящие на главной диагонали, равны нулю, называется диагональной.
Определение 7. Диагональная матрица, у которой все отличные от нуля элементы, единицы, называется единичной Е.
Например,  .
.
Определение 8. Квадратная матрица называется треугольной, прямоугольная – трапециевидной, если все элементы, лежащие по одну сторону одной из ее главных диагоналей – нули.
Определение 9. Матрица, состоящая из одной строки, называется матрицей-строкой. Матрица, состоящая из одного столбца, называется матрицей-столбцом.
Определители
Определение 13. Определителем квадратной матрицы А называется число, которое обозначается символом  или
или 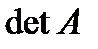 или
или 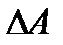 или
или  и вычисляется по некоторым правилам, в зависимости от размерности матрицы.
и вычисляется по некоторым правилам, в зависимости от размерности матрицы.
Правила вычисления определителей
1. Определитель квадратной матрицы порядка n = 1:
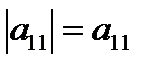 Пример.
Пример. 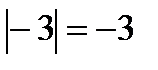
2.Определитель квадратной матрицы порядка n = 2:
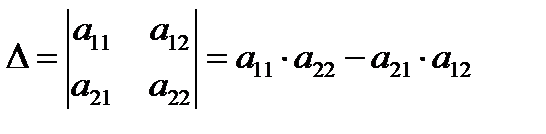
Пример.  .
.
3. Определитель квадратной матрицы порядка n = 3:
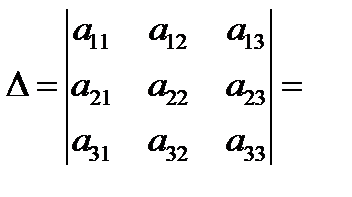
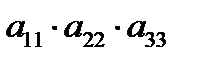 +
+ 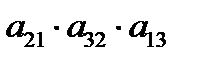 +
+ 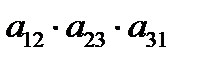 –
– 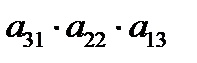 –
–  –
– 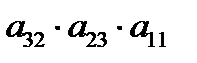 – правило треугольников.
– правило треугольников.
Пример.
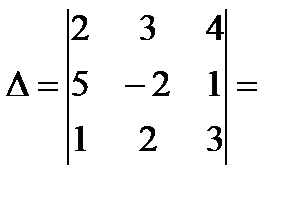
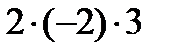 +
+  +
+ 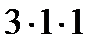 –
–  –
–  –
– 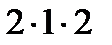 = – 10.
= – 10.
4. Определитель квадратной матрицы порядка n вычисляется либо методом понижения порядка, либо методом приведения к треугольному виду.
Рассмотрим вычисление определителя методом понижения порядка. Прежде, чем его рассмотреть, отметим ряд свойств определителя и дадим несколько определений.
Свойства определителя
1. Определитель не изменяется при транспонировании.
2. При перестановке двух строк (столбцов) определитель меняет знак.
3. Если две строки (столбца) определителя совпадают, то он равен нулю.
4. Если все элементы какой-нибудь строки (столбца) определителя имеют общий множитель, то его можно вынести за знак определителя.
5. Если все элементы какой-нибудь строки (столбца) определителя есть нули, то det А = 0.
6. Если элементы двух строк (столбцов) взаимно пропорциональны, то det А = 0.
7. Если каждый элемент некоторой строки определителя представляет собой сумму двух слагаемых, то определитель представляется в виде суммы двух определителей, у которых элементы рассматриваемой строки в первом определителе равны первым слагаемым, во втором – вторым. (Аналогично со столбцами). Например, 

8. Определитель не изменится, если к элементам одной строки (столбца) прибавить другую строку (столбец), умноженную на действительное число.
9. Определитель треугольной матрицы равен произведению элементов, стоящих на ее главной диагонали.
Определение 14. Минором 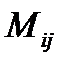 определителя, соответствующим элементу
определителя, соответствующим элементу 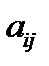 называется определитель, получаемый из данного вычеркиванием строки и столбца, на пересечении которых стоит данный элемент.
называется определитель, получаемый из данного вычеркиванием строки и столбца, на пересечении которых стоит данный элемент.
Определение 15. Алгебраическим дополнением элемента 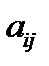 называется число, вычисляемое по формуле
называется число, вычисляемое по формуле 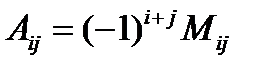 .
.
Пример. Найти 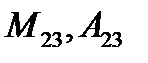 , А13,
, А13,  .
.
Решение.
Вычеркнем в определителе вторую строку и третий столбец, тогда минор 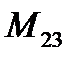
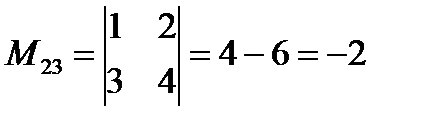 .
. 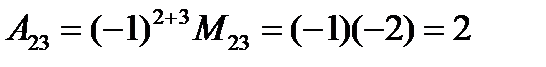 .
. 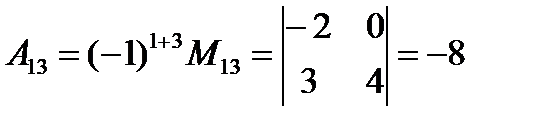 .
.
Метод понижения порядка.
Определитель равен сумме произведений элементов какой-либо строки или столбца на их алгебраические дополнения:
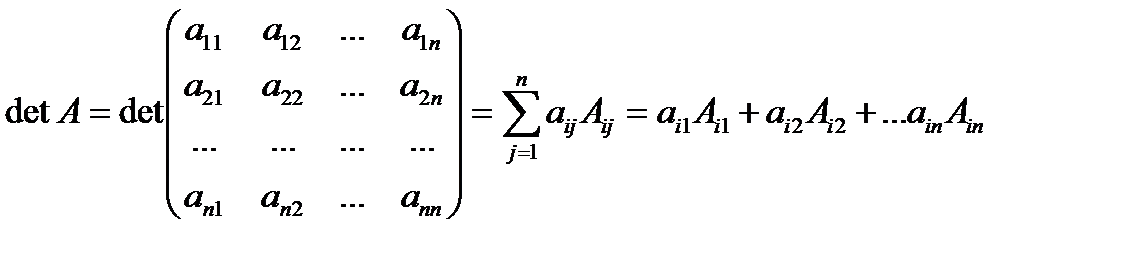 - разложение определителя по i-той строке.
- разложение определителя по i-той строке.
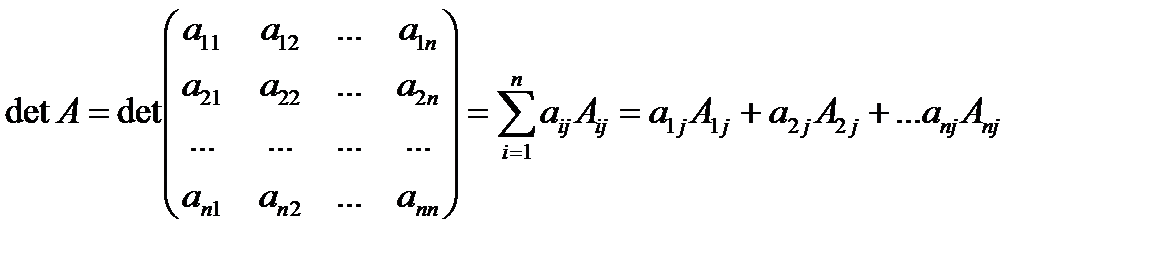 - разложение определителя по j-тому столбцу.
- разложение определителя по j-тому столбцу.
Пример. Вычислить определитель путем разложения по 1-ой строке и второму столбцу.
Решение.
По первой строке: 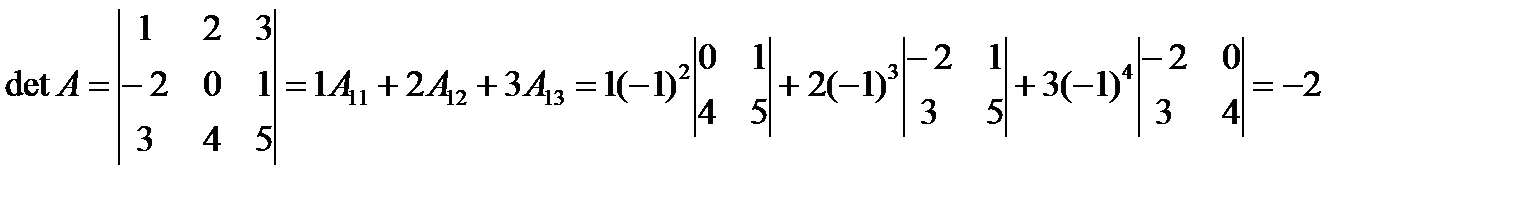 .
.
По второму столбцу: 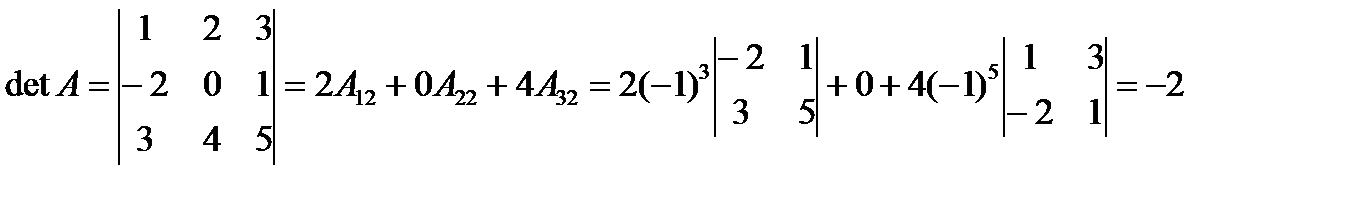 .
.
Определение 16. Матрица называется невырожденной, если ее определитель не равен нулю и вырожденной в противном случае.
Замечание (об обратной матрице). В алгебре матриц нет понятия деления матриц. Для невырожденных матриц существует обратная матрица.
Определение. Матрица 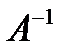 называется обратной к матрице А, если
называется обратной к матрице А, если  , где Е – единичная матрица.
, где Е – единичная матрица.
Теорема о вычислении обратной матрицы. Если А невырожденная ( 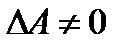 ) матрица порядка n, то обратная к ней матрица находится по формуле
) матрица порядка n, то обратная к ней матрица находится по формуле 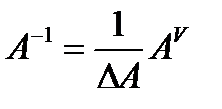 , где
, где 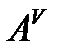 – присоединенная матрица, то есть транспонированная матрица, составленная из алгебраических дополнений.
– присоединенная матрица, то есть транспонированная матрица, составленная из алгебраических дополнений.
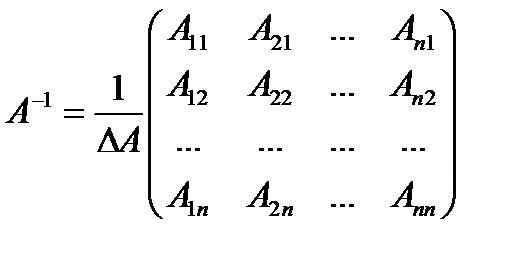
Понятие о ранге матрицы.
Определение 17. Строки матрицы А называются линейно зависимыми, если какая-либо из них линейно выражается через остальные. В противном случае – строки линейно независимы. (аналогично столбцы).
Пример. 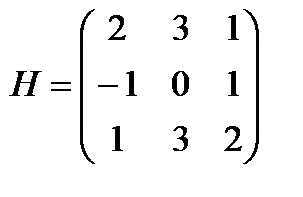 . Найти количество линейно независимых строк и столбцов.
. Найти количество линейно независимых строк и столбцов.
Решение. Обозначим строки: Е1 = (2 3 1), Е2 = (–1 0 1), Е3 = (1 3 2). Видно, что Е3 = Е1 + Е2, следовательно, Е1, Е2, Е3 – линейно зависимы. Е2 ≠ k Е1, следовательно, Е1 , Е2 – линейно независимы. Вывод: матрица имеет две линейно независимых строки.
Обозначим столбцы: F1, F2, F3. Видно, что F2 = F1 + F3, следовательно, F1, F2, F3 – линейно зависимы. F1 ≠ k F2, следовательно, F1, F2 – линейно независимы. Вывод: матрица имеет два линейно независимых столбца.
Можно доказать, что для любой матрицы максимальное число линейно независимых строк и максимальное число линейно независимых столбцов совпадают.
Определение 18. Ранг матрицы равен максимально возможному числу ее линейно независимых строк (столбцов).
Т.е. в примере rang H = 2.
Замечание. Ранг квадратной матрицы не превосходит ее порядок. Ранг равен порядку в том и только в том случае, если матрица невырожденная. Ранг матрицы размера 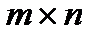 не превосходит меньшего из чисел m и n.
не превосходит меньшего из чисел m и n.
Не изменяют ранга элементарные преобразования над матрицами:
1. перестановка строк (столбцов),
2. умножение строки (столбца) на число, не равное нулю,
3. прибавление к строке (столбцу) другой строки (столбца), умноженной на число,
4. отбрасывание нулевых строк (столбцов),
5. транспонирование.
Если удастся путем элементарных преобразований привести матрицу к трапециевидной форме, то ееранг будет равен числу ее ненулевых строк!
При приведении матрицы к трапециевидной форме удобно пользоваться численным методом Гаусса:
1) переставляя строки, добиваемся, чтобы 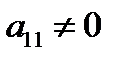 и
и 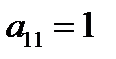 , последнее можно достичь (если в первом столбце нет единиц) путем деления всей строки на
, последнее можно достичь (если в первом столбце нет единиц) путем деления всей строки на  . Первую строку называют рабочей, а элемент
. Первую строку называют рабочей, а элемент  – ведущим.
– ведущим.
2) умножаем первую строку на числа (  ), где
), где 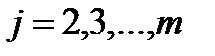 , прибавляем ее соответственно ко второй и т.д. m-ой строке, получаем в 1-ом столбце под
, прибавляем ее соответственно ко второй и т.д. m-ой строке, получаем в 1-ом столбце под 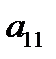 нули.
нули.
3) не трогая первой строки, добиваемся, чтобы 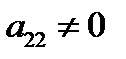 и
и 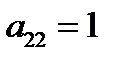 путем деления всей строки на
путем деления всей строки на  или путем перестановки строк. Теперь вторая строка стала рабочей, а элемент
или путем перестановки строк. Теперь вторая строка стала рабочей, а элемент 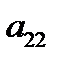 – ведущим.
– ведущим.
4) умножаем вторую строку на числа ( 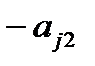 ), где
), где 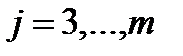 , прибавляем ее соответственно к третей и т.д. m-ой строке, получаем во 2-ом столбце под
, прибавляем ее соответственно к третей и т.д. m-ой строке, получаем во 2-ом столбце под  нули.
нули.
5) и т.д.
Пример. Найти ранг матрицы 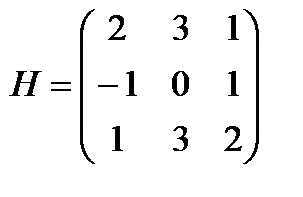 . Решение.
. Решение. 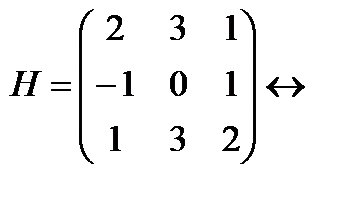 (меняем строки местами)
(меняем строки местами)  (первую строку прибавляем ко второй)
(первую строку прибавляем ко второй) 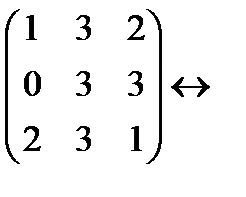 (первую строку умножаем на (-2) и прибавляем к третьей)
(первую строку умножаем на (-2) и прибавляем к третьей) 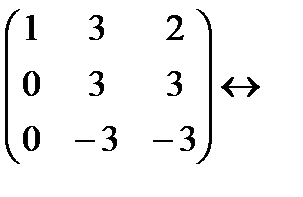 (прибавляем ко второй строке третью)
(прибавляем ко второй строке третью) 
 ,
,
Две ненулевые строки, то есть rang H = 2.
Системы линейных уравнений.
П. 1. Основные понятия.
Определение 19. Система уравнений вида  называется системой m линейных уравнений с n неизвестными
называется системой m линейных уравнений с n неизвестными 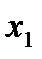 ,
,  , …,
, …, 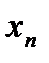 .
.
Если все bi = 0 ( i = 1, 2, 3,…, m), то система называется однородной, в противном случае неоднородной.
Матрица, состоящая из коэффициентов при неизвестных, называется матрицей системы. Матрица, состоящая из коэффициентов при неизвестных и столбца свободных членов, называется расширенной матрицей системы.
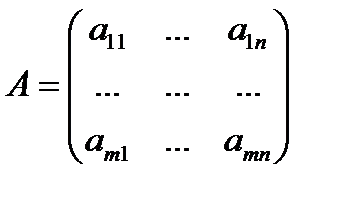 – матрица системы,
– матрица системы, 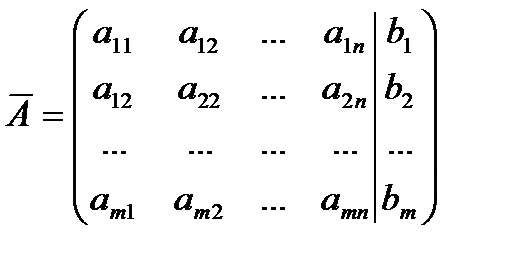 – расширенная матрица системы,
– расширенная матрица системы,
 – столбец свободных членов,
– столбец свободных членов, 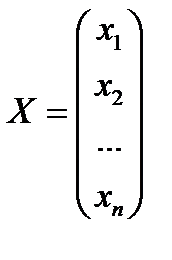 – столбец неизвестных.
– столбец неизвестных.
Матричная запись системы линейных уравнений имеет вид: 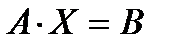 .
.
Определение 20. Система уравнений, имеющая хотя бы одно решение, называется совместной. Система, не имеющая решений, несовместной.
Элементарные преобразования системы (только над строками):
1. перестановка уравнений,
2. умножение уравнения на число, отличное от нуля,
3. прибавление к уравнению другого уравнения, умноженного на число.
Выполняют элементарные преобразования над расширенной матрицей системы и лишь над строками, так как перестановка столбцов соответствует переобозначению неизвестных.
Пп. 1. Метод Гаусса
(для решения однородных и неоднородных систем, когда  )
)
 - неоднородная,
- неоднородная, 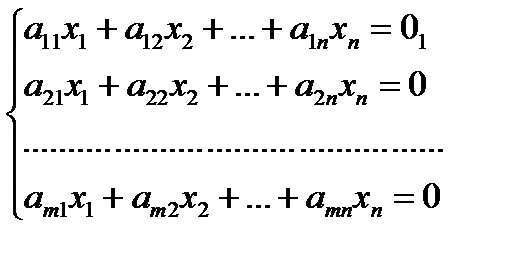 - однородная.
- однородная.
Метод заключается в последовательном исключении неизвестных, с помощью элементарных преобразований над строками расширенная матрица системы приводится к трапециевидной или к треугольной форме, при этом удобнее, чтобы все ведущие элементы были равны 1 (алгоритм нахождения рангов), либо устанавливается, что система несовместна. Это прямой ход метода Гаусса.
Прямой ход метода Гаусса:
1. Записываем расширенную матрицу системы  .
.
2. Переставляя строки, добиваемся, чтобы 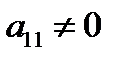 ; удобнее, чтобы
; удобнее, чтобы  и, если в первом столбце есть 1, то именно эту строку делаем первой. Первую строку назовем рабочей, элемент
и, если в первом столбце есть 1, то именно эту строку делаем первой. Первую строку назовем рабочей, элемент 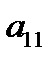 - ведущим.
- ведущим.
3. Ведущий элемент рабочей строки должен быть равен 1. Если 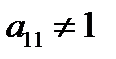 , то делим первую строку на
, то делим первую строку на 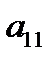 .
.
4. Умножая первую строку на числа 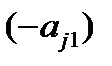 , где
, где  , и прибавляя ее соответственно ко второй и т.д. m-ой строке, получим в 1-ом столбце под
, и прибавляя ее соответственно ко второй и т.д. m-ой строке, получим в 1-ом столбце под 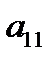 нули. 5. Не трогая первой строки, путем перестановки остальных строк, добиваемся, чтобы
нули. 5. Не трогая первой строки, путем перестановки остальных строк, добиваемся, чтобы 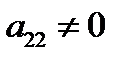 , а лучше, если во втором столбце, кроме первой строки, есть 1, чтобы
, а лучше, если во втором столбце, кроме первой строки, есть 1, чтобы 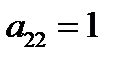 , (рабочей стала вторая строка, ведущим – элемент
, (рабочей стала вторая строка, ведущим – элемент  ).
).
6. Если  , то делим вторую строку на
, то делим вторую строку на 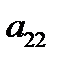 , получим ведущий элемент равным 1.
, получим ведущий элемент равным 1.
7. Умножая вторую строку на числа  , где
, где 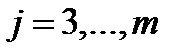 , и прибавляя ее соответственно к третьей и т.д. m-ой строке, получим во 2-ом столбце под
, и прибавляя ее соответственно к третьей и т.д. m-ой строке, получим во 2-ом столбце под  нули.
нули.
8. И так далее, пока расширенная матрица системы не приведется к трапециевидной форме. На главной диагонали полученной матрицы стоят единицы.
Например, 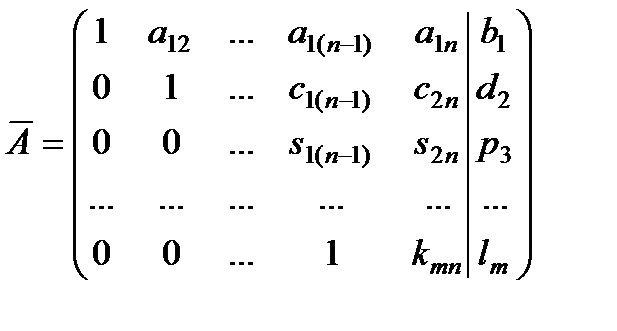 .
.
9. Находим ранги матрицы-системы и расширенной матрицы системы. Проверяем условия теоремы Кронекера-Капелли. Делаем вывод о количестве решений системы: одно решение, либо бесконечное множество решений, или нет решений.
Обратный ход заключается в последовательном нахождении неизвестных. Для этого полученная трапециевидная или треугольная матрица записывается снова в виде системы уравнений, и из нее алгебраическим путем, начиная с последнего уравнения, находятся неизвестные.
В нашем примере получаем бесконечное множество решений, которые находятся из системы:
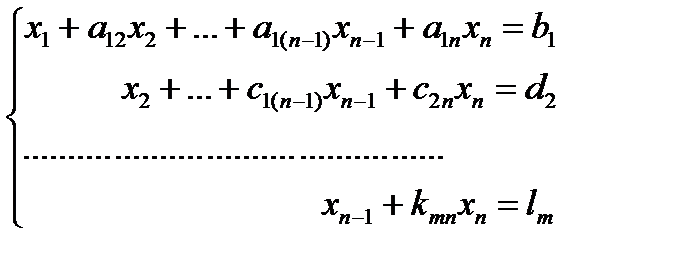 .
.
В случае бесконечного множества решений все переменные делятся на базисные и свободные.
Определение 21. Базисным минором называется ненулевой минор максимального порядка основной матрицы, находящийся в левом верхнем углу. Базисные переменные – это переменные, коэффициенты при которых образуют базисный минор. Остальные переменные называются свободными, т.е. это переменные, которым можно придавать произвольные действительные значения.
Количество базисных переменных равно 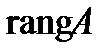 .
.
Количество свободных переменных можно найти с помощью формулы: 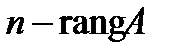 .
.
Все получившиеся базисные переменные (в примере 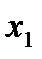 ,
,  , …,
, …,  ) выражаются через свободные (в примере
) выражаются через свободные (в примере 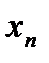 ) и находится решение системы, либо, если все переменные являются базисными, то выражается в численном виде единственное решение системы линейных уравнений.
) и находится решение системы, либо, если все переменные являются базисными, то выражается в численном виде единственное решение системы линейных уравнений.
Эта процедура начинается с последнего уравнения, из которого выражают соответствующую базисную переменную (а она там всего одна) и подставляют в предыдущие уравнения, и так далее, поднимаясь по «ступенькам» наверх. Каждой строчке соответствует ровно одна базисная переменная, поэтому на каждом шаге, кроме последнего (самого верхнего), ситуация в точности повторяет случай последней строки.
В примере:  , …,
, …, 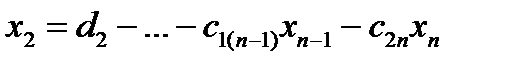 ,
,  .
.
Ответ примера: {( 
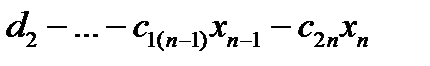 , … ,
, … , 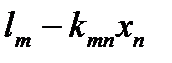 ),
), 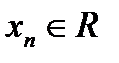 }.
}.
Определение 22. Базисным решением называется частное решение, получающееся из общего при нулевых значениях свободных переменных.
Пп. 2. Метод Крамера
(для решения неоднородных систем, когда 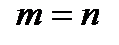 )
)
Замечание. Метод применяется (редко) для решения и однородных систем, в случае, когда 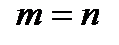 . Будет рассмотрено в замечании к теореме Крамера.
. Будет рассмотрено в замечании к теореме Крамера.
Теорема Крамера. Рассмотрим неоднородную систему n линейных уравнений с n неизвестными 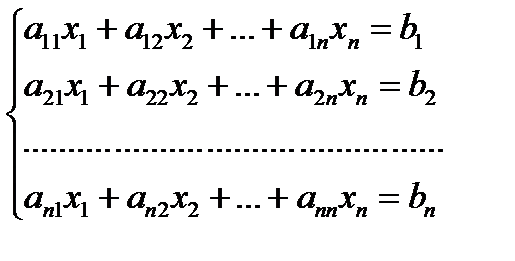 . Если определитель матрицы системы отличен от нуля, то система имеет единственное решение, которое находится по формулам:
. Если определитель матрицы системы отличен от нуля, то система имеет единственное решение, которое находится по формулам:  ,
, 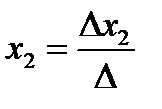 , …,
, …, 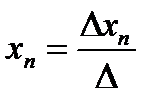 , где
, где 
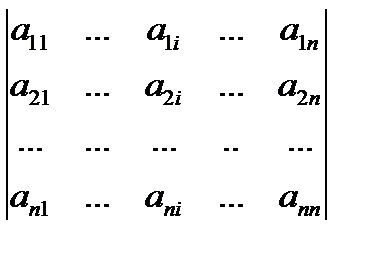 – определитель матрицы системы,
– определитель матрицы системы,  – определитель, полученный из определителя
– определитель, полученный из определителя  заменой i –того столбца столбцом свободных членов, i = 1, 2,…, n. (без доказательства)
заменой i –того столбца столбцом свободных членов, i = 1, 2,…, n. (без доказательства)
Замечание 1) Если определитель матрицы неоднородной системы 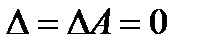 , но и все
, но и все 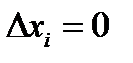 , то система имеет бесконечное множество решений, которые находятся по формулам:
, то система имеет бесконечное множество решений, которые находятся по формулам:  , где В i – алгебраические дополнения к элементам той строки, где стоит элемент, минор которого отличен от нуля.
, где В i – алгебраические дополнения к элементам той строки, где стоит элемент, минор которого отличен от нуля.
Если 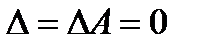 , но при этом хотя бы один из
, но при этом хотя бы один из  , то система не имеет решений.
, то система не имеет решений.
Замечание 2) Метод Крамера можно применить и для решения однородных систем линейных уравнений, когда 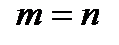 .
.
Если 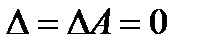 , но хотя бы один из его миноров отличен от нуля, то система имеет бесконечное множество решений, которые находятся по формулам:
, но хотя бы один из его миноров отличен от нуля, то система имеет бесконечное множество решений, которые находятся по формулам:  , где В i – алгебраические дополнения к элементам той строки, где стоит элемент, минор которого отличен от нуля.
, где В i – алгебраические дополнения к элементам той строки, где стоит элемент, минор которого отличен от нуля.
Если 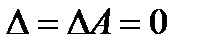 и все его миноры равны нулю, то система сводится к одному уравнению и имеет бесконечное множество решений.
и все его миноры равны нулю, то система сводится к одному уравнению и имеет бесконечное множество решений.
Если 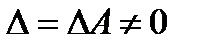 , то система имеет единственное решение - нулевое.
, то система имеет единственное решение - нулевое.
Пример 1. Решить систему уравнений:  .
.
Решение. Найдем определитель матрицы системы: 
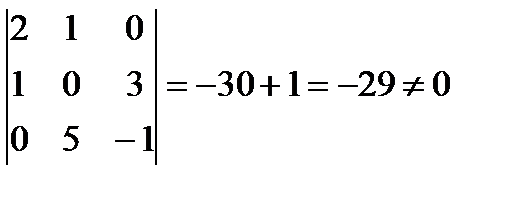 , следовательно, система имеет единственное решение.
, следовательно, система имеет единственное решение.
Найдем определители  :
:
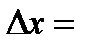
 ,
, 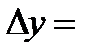
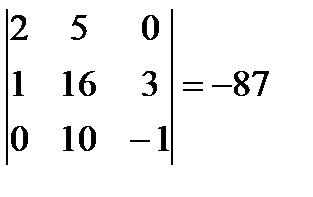 ,
, 
 .
.
Найдем решение системы по формулам Крамера:
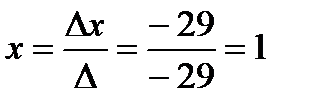 ,
, 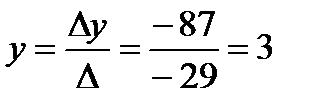 ,
, 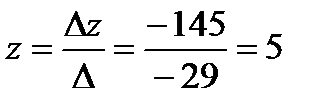 .
.
Ответ: {(1, 3, 5)}.
Пример 2. Решить систему уравнений: 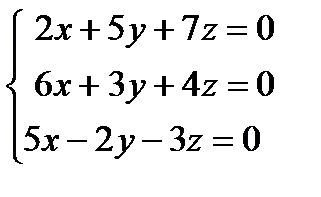 .
.
Решение. Данная однородная система имеет 3 уравнения с тремя неизвестными. Для нахождения решения применим замечание 2 к теореме Крамера.
Найдем определитель матрицы системы: 
 , следовательно, система имеет единственное решение - нулевое.
, следовательно, система имеет единственное решение - нулевое.
Ответ: {(0, 0, 0)}.
Примеры.
Пример 1. Решить систему линейных уравнений 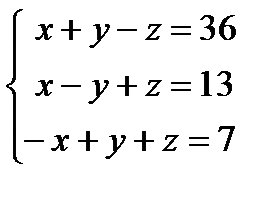 двумя способами.
двумя способами.
Решение.
1. Метод Гаусса.
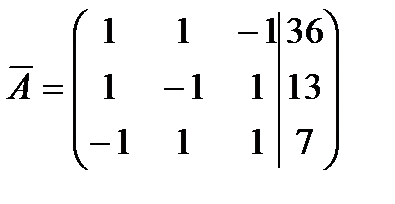



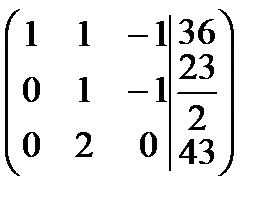

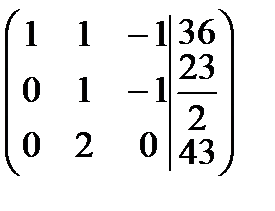




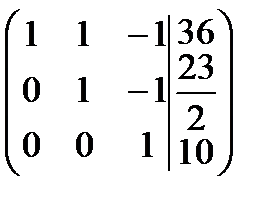
Найдем ранги матрицы системы и расширенной матрицы системы:  , число неизвестных n = 3, следовательно,
, число неизвестных n = 3, следовательно,  , отсюда по теореме Кронекера-Капелли система имеет единственное решение.
, отсюда по теореме Кронекера-Капелли система имеет единственное решение.
Найдем его. Для этого запишем полученную матрицу в виде системы линейных уравнений:
 .
.
Отсюда 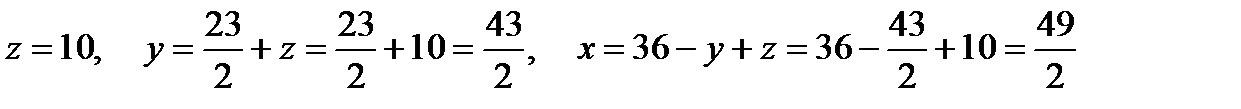 .
.
Ответ: 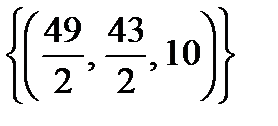 .
.
2) Метод Крамера.
Найдем определитель матрицы системы: 
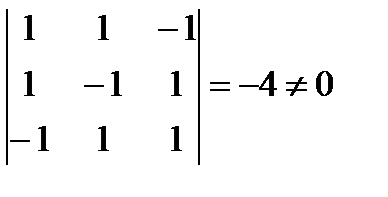 , следовательно, существует единственное решение. Найдем определители
, следовательно, существует единственное решение. Найдем определители  :
:
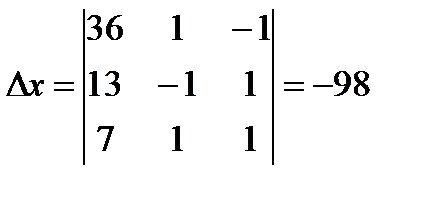 ,
, 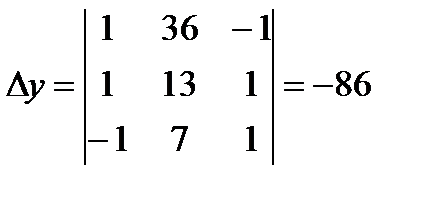 ,
, 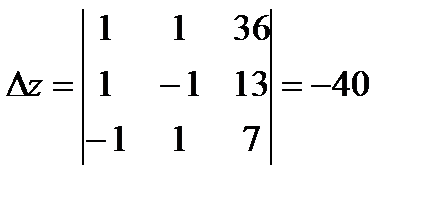 .
.
По формулам Крамера решение системы имеет вид:
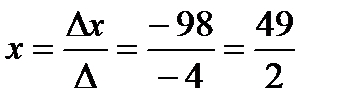 ,
, 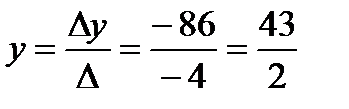 ,
, 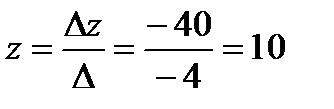 .
.
Ответ: 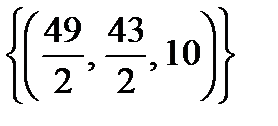 .
.
Пример 2. Решить систему линейных уравнений 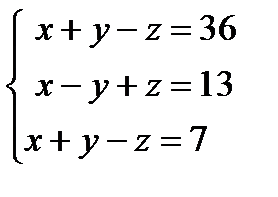 методом Гаусса.
методом Гаусса.
Решение.
1. Метод Гаусса.


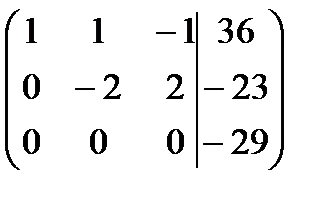 .
.
Найдем ранги матрицы системы и расширенной матрицы системы:  , следовательно,
, следовательно, 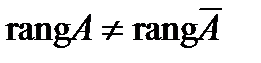 , отсюда по теореме Кронекера-Капелли система не имеет решений.
, отсюда по теореме Кронекера-Капелли система не имеет решений.
Ответ: система не имеет решений.
Пример 3. Решить систему линейных уравнений  .
.
В случае бесконечного множества решений, найти базисное решение.
Решение.
Данную систему можно решить только методом Гаусса, так как количество переменных больше, чем уравнений.







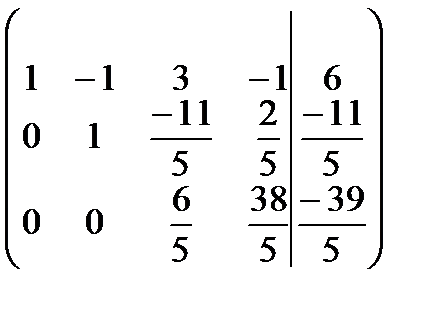


Найдем ранги матрицы системы и расширенной матрицы системы:  , число неизвестных n = 4, следовательно,
, число неизвестных n = 4, следовательно, 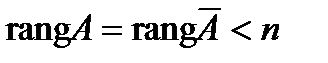 , отсюда по теореме Кронекера-Капелли система имеет бесконечное множество решений. Найдем его. Для этого запишем полученную матрицу в виде системы уравнений:
, отсюда по теореме Кронекера-Капелли система имеет бесконечное множество решений. Найдем его. Для этого запишем полученную матрицу в виде системы уравнений:
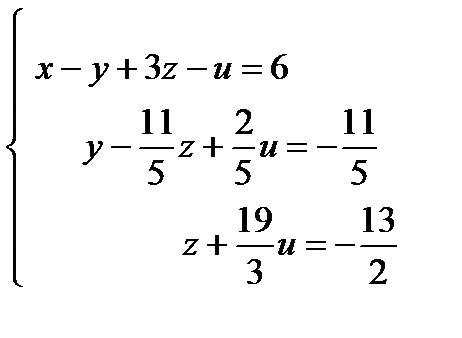
Введем одну свободную переменную, пусть это будет u, и выразим через нее все оставшиеся неизвестные.
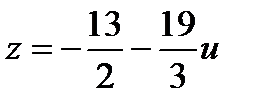 ,
, 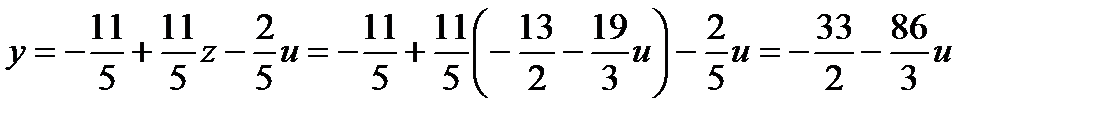 ,
,
 .
.
Ответ: 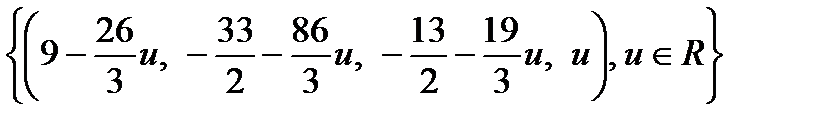 . Базисным решением называется частное решение, получающееся из общего при нулевых значениях свободных переменных, то есть
. Базисным решением называется частное решение, получающееся из общего при нулевых значениях свободных переменных, то есть 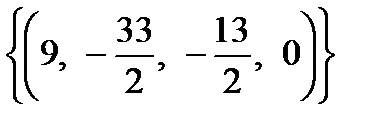 .
.
Глава 2. Векторная алгебра.
Векторы.
П.1. Основные определения.
Существуют скалярные и векторные величины. Скалярные характеризуются своим численным значением (например, температура, работа, плотность,…), а векторные, кроме численного значения, обладают также направлением в пространстве (например, сила, скорость,…).
Определение 1. Вектором называется направленный отрезок 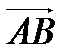 с начальной точкой А и конечной В.
с начальной точкой А и конечной В. 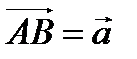
| В |
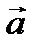
|
| А |
Определение 2. Длиной вектора  называется длина отрезка
называется длина отрезка  . Число, равное длине вектора, измеренного выбранной масштабной единицей, называется модулем.
. Число, равное длине вектора, измеренного выбранной масштабной единицей, называется модулем. 
Задать вектор – это значит задать его модуль и направление в пространстве.
Определение 3. Вектор 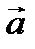 называется единичным, если
называется единичным, если 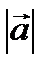 =1. Вектор
=1. Вектор  называется нулевым или нуль-вектором, если
называется нулевым или нуль-вектором, если 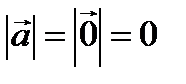 . Нулевой вектор
. Нулевой вектор 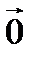 имеет любое направление.
имеет любое направление.
Определение 4. Векторы 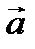 и
и  называются сонаправленными, если они параллельны (лежат на одной или параллельных прямых) и имеют одинаковое направление, если при этом направление не совпадает, то векторы называются противоположно направленными.
называются сонаправленными, если они параллельны (лежат на одной или параллельных прямых) и имеют одинаковое направление, если при этом направление не совпадает, то векторы называются противоположно направленными.
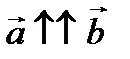 – сонаправлены.
– сонаправлены. 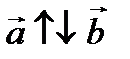 – противоположно направлены.
– противоположно направлены.
Определение 5. Векторы 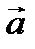 и
и  называются равными, если
называются равными, если 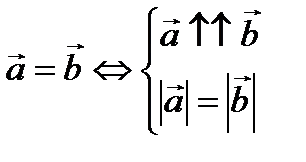 .
.
Определение 6. Единичный вектор, имеющий одинаковое направление с вектором 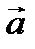 , называется ортом вектора
, называется ортом вектора 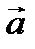 и обозначается
и обозначается 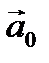 .
.
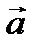
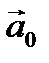
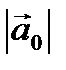 =1.
=1.
Определение 7. Вектор, выходящий из начала координат, называется радиус-вектором.
С помощью параллельного переноса векторы можно перемещать в любое место пространства.
Вычитание векторов.
Определение 8. Противоположным вектором к вектору 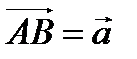 называется вектор
называется вектор 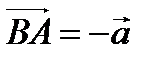 , причем
, причем 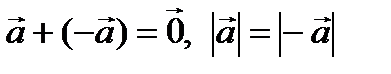 .
.
Вычесть вектор, значит прибавить противоположный.
|
|

|
– 
|
А) Правило параллелограмма.
|
|

|
В) Правило треугольника
Вывод из 1 и 2: векторы суммы и разности векторов направлены по диагоналям параллелограмма, построенного на векторах 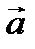 и
и  .
.
|
|
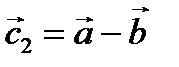
|
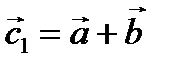
|
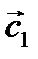
|
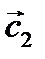
|
Замечания.
1. В плоскости базисом могут служить любые два непараллельных вектора.
2. В пространстве базисом могут служить любые три вектора, не параллельных одной плоскости, то есть некомпланарных.
Например, в пространстве R3 одним из базисов является совокупность векторов 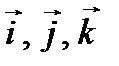 - ортов координатных осей.
- ортов координатных осей.
Определение 23. Разложение вектора 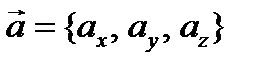 по ортам
по ортам  :
: 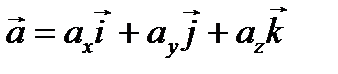 называется разложением вектора по базису
называется разложением вектора по базису 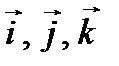 .
.
Пример. Найти разложение вектора 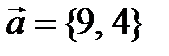 1) по базису векторов
1) по базису векторов 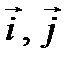 , 2) по базису векторов
, 2) по базису векторов 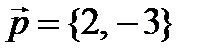 и
и 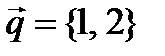 .
.
Решение.
1) Разложение вектора 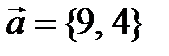 по базису векторов
по базису векторов 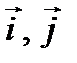 имеет вид:
имеет вид: 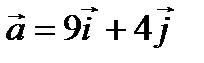 .
.
2) Векторы 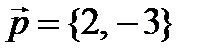 и
и 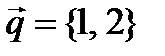 не коллинеарны, так как
не коллинеарны, так как 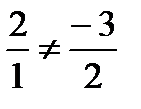 , следовательно, образуют базис. Вектор
, следовательно, образуют базис. Вектор  представляет собой линейную комбинацию векторов
представляет собой линейную комбинацию векторов  и
и 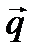 :
: 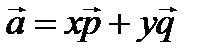 , где числа х и у – коэффициенты линейной комбинации. Найдем их. Для этого составим систему:
, где числа х и у – коэффициенты линейной комбинации. Найдем их. Для этого составим систему:

 . Отсюда у = 5, х = 2.
. Отсюда у = 5, х = 2.
Следовательно, 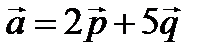 - разложение вектора
- разложение вектора 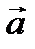 по базису векторов
по базису векторов 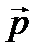 и
и 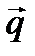 .
.
Проиллюстрируем пример. Изобразим векторы на плоскости.
|
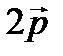
|
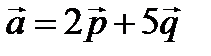
|
| х |
| у |
| О |
| х |
| у |
| О |
| 9 |
| 4 |
| 2 |
| -3 |
| 2 |
| 1 |
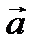
|
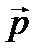
|
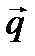
|
По правилу параллелограмма найдем сумму двух векторов
 и
и  :
:
Проекции вектора на вектор
Известно, что проекция вектора на ось l вычисляется по формуле Пр l  =
= 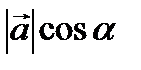 , где
, где 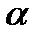 - угол между вектором и осью. Пусть вектор
- угол между вектором и осью. Пусть вектор 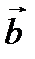 лежит на оси l и сонаправлен с ней. Тогда
лежит на оси l и сонаправлен с ней. Тогда 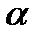 - угол между векторами
- угол между векторами 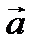 и
и 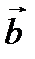 . Проекция вектора
. Проекция вектора 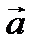 на вектор
на вектор 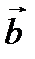 вычисляется по формуле: Пр
вычисляется по формуле: Пр 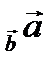 =
= 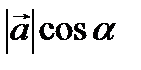 .
.
Домножим обе части равенства на  , получим:
, получим:
 Пр
Пр 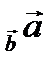 =
= 
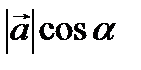 , тогда, по определению,
, тогда, по определению,  Пр
Пр 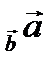 =
= 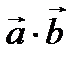 . Отсюда,
. Отсюда,
Пр 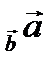 =
=  или Пр
или Пр 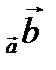 =
= 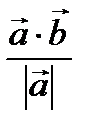 . (3)
. (3)
Таблица скалярного умножения ортов

|
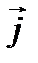
|
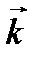
|
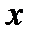
|
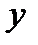
|

|
| 1 |
| 1 |
| 1 |
| O |
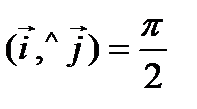 ,
, 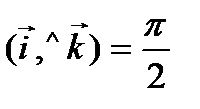 ,
, 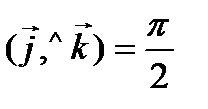 ,
, 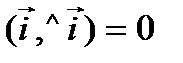 ,
, 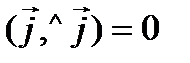 ,
,
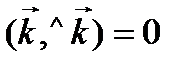 ; тогда
; тогда 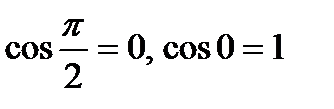 ; длины ортов равны
; длины ортов равны 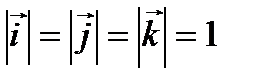 .
.
Следовательно, исходя из определения скалярного произведения, можем записать, что
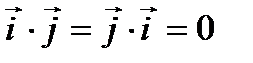 ,
, 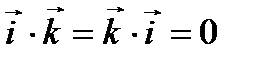 ,
, 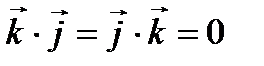 ,
, 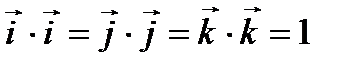 .
.
Примеры.
Пример 1. Найти скалярное произведение векторов 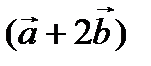 и
и  , если известно, что
, если известно, что 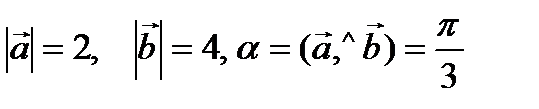 .
.
Решение. 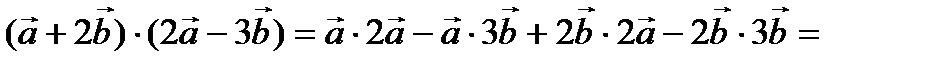
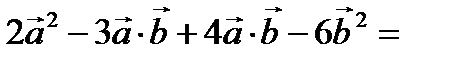
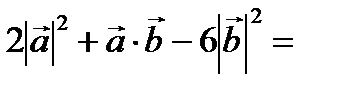
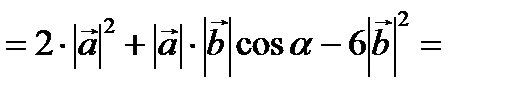
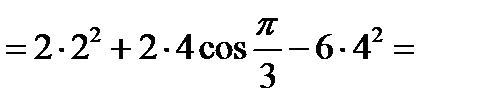 –84.
–84.
Пример 2. Даны вершины треугольника АВС, где А(–1, –2, 4), В(–4, –2, 0), С(3, –2, 1). Определить его внутренний угол α при вершине В.
Решение.
Угол при вершине В образуют вектора  и
и  ,
, 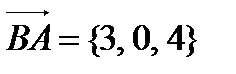 ,
, 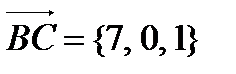 . Длины векторов равны
. Длины векторов равны 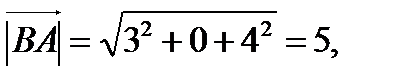
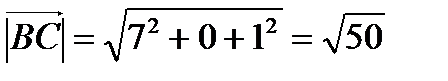 , тогда по формуле (7):
, тогда по формуле (7): 
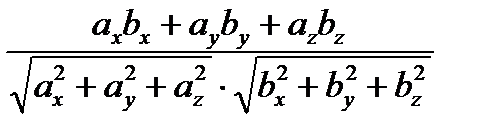 =
= 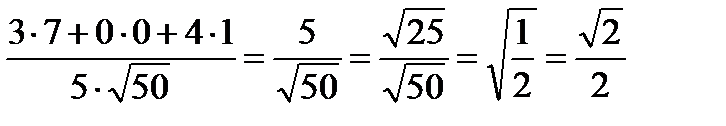 , то есть α = 450.
, то есть α = 450.
Пример 3. Проверить перпендикулярность векторов 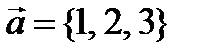 и
и 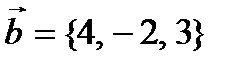 .
.
Решение. 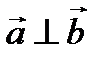
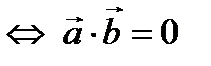 . Найдем
. Найдем  , то есть векторы не перпендикулярны.
, то есть векторы не перпендикулярны.
Таблица векторного умножения ортов

|
|
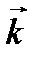
|
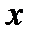
|
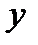
|

|
| 1 |
| 1 |
| 1 |
| O |
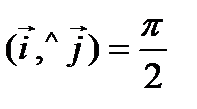 ,
, 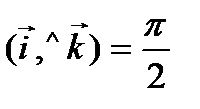 ,
, 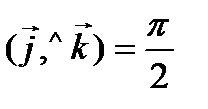 ,
, 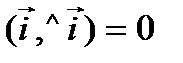 ,
, 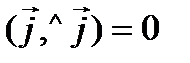 ,
,
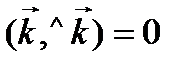 ; тогда
; тогда  ; длины ортов равны
; длины ортов равны 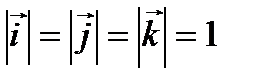 .
.
Следовательно, исходя из определения векторного произведения, можем записать, что 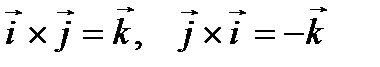 ,
,  ,
, 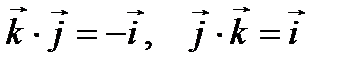 ,
, 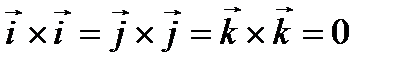 .
.
Примеры.
Пример № 1. Векторы 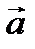 и
и 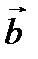 образуют угол
образуют угол  . Зная
. Зная 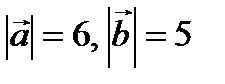 , вычислить
, вычислить  .
.
Решение.  =
= 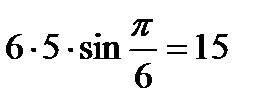 . Ответ: 15.
. Ответ: 15.
Пример № 2. Даны 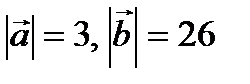 ,
,  . Вычислить
. Вычислить 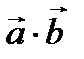 .
.
Решение. Из свойства 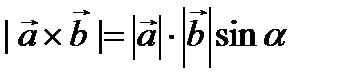 выразим
выразим 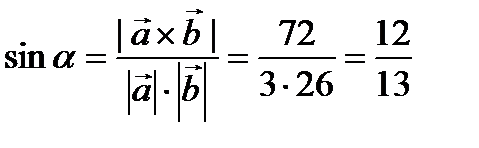 .
.
Из основного тригонометрического тождества следует, что 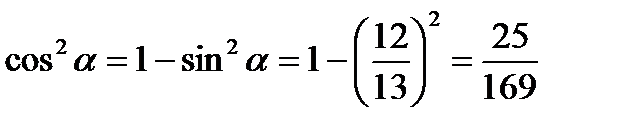 .
.
Найдем 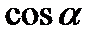 :
:  . По определению найдем скалярное произведение векторов:
. По определению найдем скалярное произведение векторов: 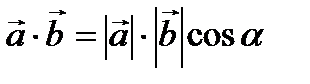 =
= 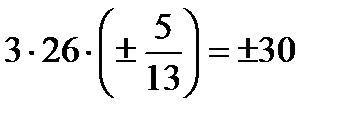
Пример № 3. Векторы 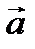 и
и 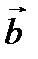 образуют угол
образуют угол 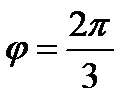 . Зная
. Зная 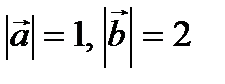 , вычислить
, вычислить  .
.
Решение.
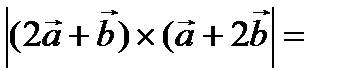
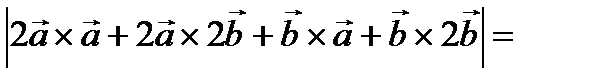

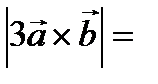 3
3 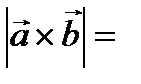
=  .
.
Пример № 4. Даны два вектора  и
и 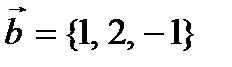 . Найти координаты векторного произведения векторов
. Найти координаты векторного произведения векторов 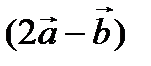 и
и 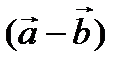 .
.
Решение.
Найдем координаты векторов 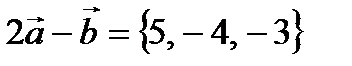 ,
, 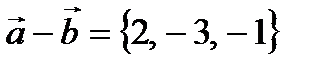 .
.
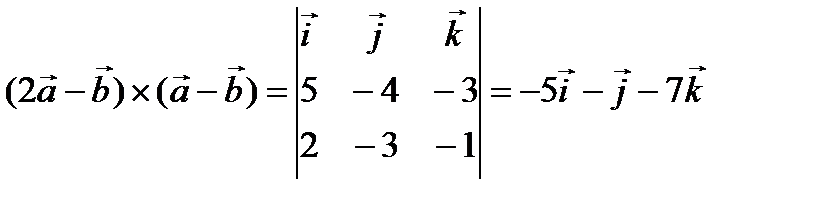 . Ответ:
. Ответ: 
Пример № 5. Сила 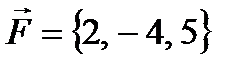 приложена к точке В(4, -2, 3). Определить момент этой силы относительно точки А(3, 2, -1) и его величину.
приложена к точке В(4, -2, 3). Определить момент этой силы относительно точки А(3, 2, -1) и его величину.
Решение.
Найдем вектор 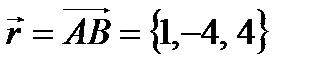 .
.
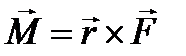 =
=  .
.
 . Ответ:
. Ответ: 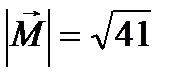
Пример № 6. Даны три вершины параллелограмма ABCD: А(2, -1, 2), В(1, 2, -1), С(3, 2, 1). Найти его площадь.
Решение.
Найдем векторы, на которых построен параллелограмм: 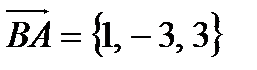 ,
, 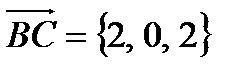 (они должны выходить из одной точки).
(они должны выходить из одной точки).
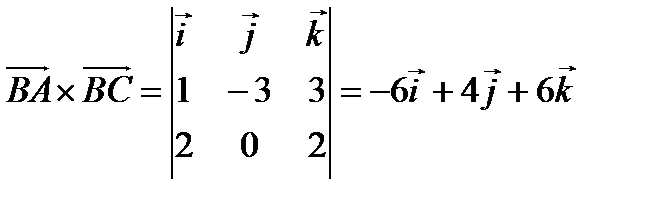 . Тогда
. Тогда 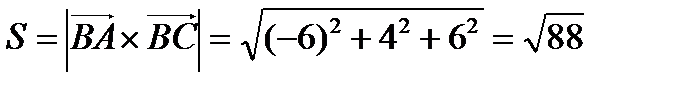 ед.кв..
ед.кв..
§ 4. Смешанное произведение векторов
Определение. Смешанным или векторно-скалярным произведением трех векторов называется число, равное 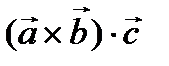 .
.
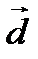
|
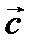
|
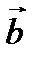
|
 по определению =
по определению = 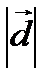 Пр
Пр 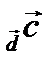 .
.
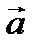
|
 , а
, а 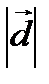 - площадь параллелограмма, построенного на векторах
- площадь параллелограмма, построенного на векторах
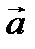 и
и  . Вектор
. Вектор  по определению векторного произведения перпендикулярен к векторам
по определению векторного произведения перпендикулярен к векторам 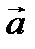 и
и  , следовательно, перпендикулярен плоскости параллелограмма. Построим на векторах
, следовательно, перпендикулярен плоскости параллелограмма. Построим на векторах  параллелепипед. Тогда Пр
параллелепипед. Тогда Пр 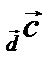 - это высота данного параллелепипеда: Пр
- это высота данного параллелепипеда: Пр 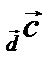 = h. Из всего вышесказанного получили, что
= h. Из всего вышесказанного получили, что 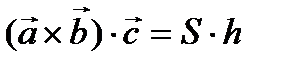 = V – объем параллелепипеда, причем
= V – объем параллелепипеда, причем  , если
, если  образуют правую тройку (h > 0), и
образуют правую тройку (h > 0), и  , если левую (h < 0). В связи с чем, правильнее писать, что объем параллелепипеда, построенного на векторах
, если левую (h < 0). В связи с чем, правильнее писать, что объем параллелепипеда, построенного на векторах  равен
равен 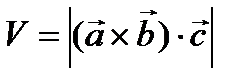 . (1)
. (1)
Свойства смешанного произведения.
1. 
При циклической перестановке множителей смешанное произведение не изменяется.
Данное свойство позволяет ввести новое обозначение смешанного произведения:  , так как результат не зависит, как расставляются скобки.
, так как результат не зависит, как расставляются скобки.
2. Условие компланарности трех векторов:
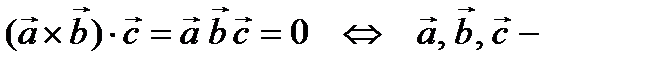 компланарные векторы. (2)
компланарные векторы. (2)
Т.е. параллелепипед вырождается в часть плоскости с нулевым объемом.
3. 
 образуют базис во множестве векторов. (3)
образуют базис во множестве векторов. (3)
Примеры.
Пример 1. Определить, какой является тройка векторов (правой или левой).
а) 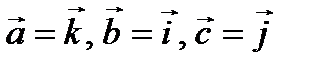 , b)
, b)  , с)
, с)  .
.
Решение: а) правая, так как поворот от вектора  к вектору
к вектору 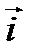 , затем к вектору
, затем к вектору  происходит против хода часовой стрелки, b) левая, так как поворот от вектора
происходит против хода часовой стрелки, b) левая, так как поворот от вектора 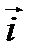 к вектору
к вектору  , затем к вектору
, затем к вектору 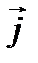 происходит по ходу часовой стрелки; с) не тройка, так как векторы компланарны.
происходит по ходу часовой стрелки; с) не тройка, так как векторы компланарны.
Пример 2. Проверить, лежат ли точки  ,
,  ,
, 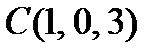 ,
, 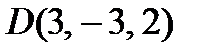 в одной плоскости.
в одной плоскости.
Решение. Составим три вектора  . Если точки лежат в одной плоскости, то векторы тоже будут лежать в одной плоскости, то есть будут компланарными.
. Если точки лежат в одной плоскости, то векторы тоже будут лежать в одной плоскости, то есть будут компланарными.
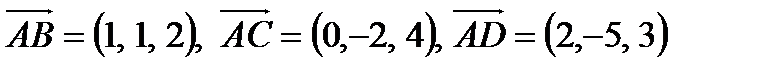 . Найдем смешанное произведение векторов:
. Найдем смешанное произведение векторов:
 , следовательно, векторы не компланарны, и точки не лежат в одной плоскости.
, следовательно, векторы не компланарны, и точки не лежат в одной плоскости.
Пример 3. Проверить, образуют ли векторы  ,
, 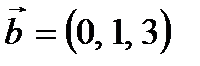 ,
, 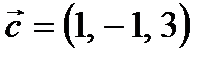 базис во множестве векторов в пространстве.
базис во множестве векторов в пространстве.
Решение. Три вектора образуют базис тогда и только тогда, когда они не компланарны. Условие компланарности векторов:  .
.
Найдем смешанное произведение векторов: 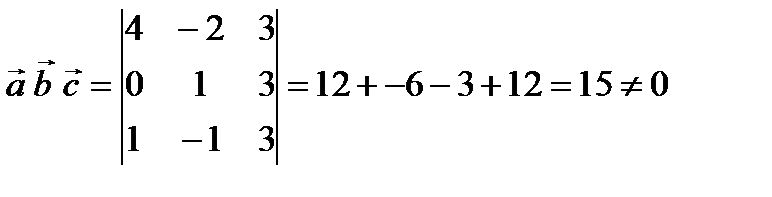 , следовательно, векторы не компланарны, и векторы образуют базис.
, следовательно, векторы не компланарны, и векторы образуют базис.
Пример 4. Найти объем пирамиды, построенной на векторах 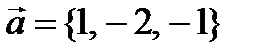 ,
,  ,
,  .
.
Решение. Vпир.= 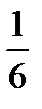 Vпарал. , Vпарал.=
Vпарал. , Vпарал.= 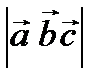 .
.  , отсюда, Vпарал.=
, отсюда, Vпарал.= 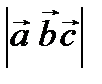 = 3, тогда Vпир.=
= 3, тогда Vпир.=  .
.
Расположение двух прямых
1) Условие параллельности двух прямых:  (координаты пропорциональны
(координаты пропорциональны  ) или
) или 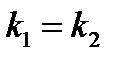 .
.
2) Условие перпендикулярности двух прямых:  (
( 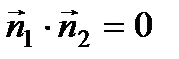 ) или
) или  .
.
3) Угол между прямыми  и
и 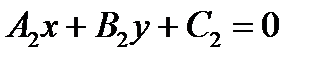
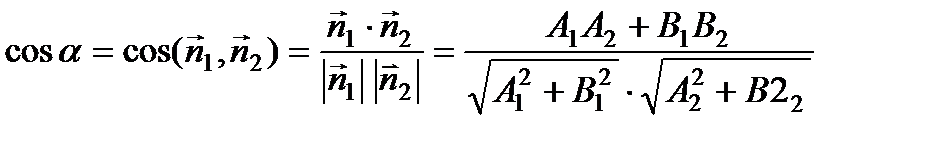 или
или 
Точка пересечения прямых находится как: 
4. Уравнение прямой, проходящей через две заданные точки 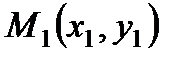 и
и 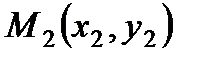 :
:
 . (4)
. (4)
5. Уравнение прямой в отрезках: 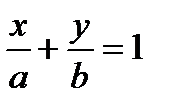 , (5)
, (5)
где a и b – величины направляющих отрезков, отсекаемых прямой на координатных осях (Ох) и (Оу) соответственно.
6. Каноническое уравнение прямой 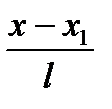
 , (6)
, (6)
т.е. уравнение прямой, проходящей через данную точку 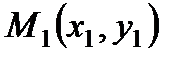 параллельно заданному вектору
параллельно заданному вектору 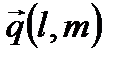 .
.
 – направляющий вектор прямой.
– направляющий вектор прямой.
7. Параметрические уравнения прямой 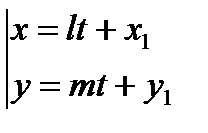 , (7)
, (7)
т.е. уравнение прямой с параметром t, проходящей через данную точку 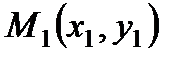 параллельно заданному вектору
параллельно заданному вектору  .
.
Нормальное уравнение прямой
| у |
| х |
| р |
| α |
| β |
| (а) |
| О |
| М0 |
| δ |
 или
или 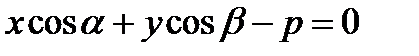 . (8)
. (8)
Если положение прямой относительно осей координат определять длиной р перпендикуляра, опущенного из начала координат на прямую и углом α, образуемым этим перпендикуляром с положительным направлением оси (Ох).
Общее уравнение прямой может быть приведено к нормальному уравнению путем домножения на нормирующий множитель 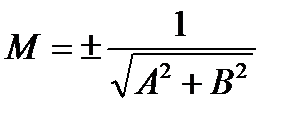 . Знак М выбирается противоположным к знаку С.
. Знак М выбирается противоположным к знаку С.
Отклонение точки М0(х0,у0) от прямой (а) вычисляется по формуле: 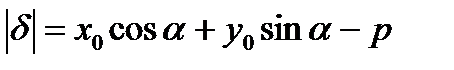 .
.
Расстояние от точки М0(х0,у0) до прямой 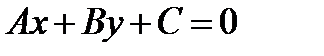
| М0 |
 М0 М0
|
| d |
 (9)
(9)
Пример 1. Дана прямая (а):  . 1) Составить уравнение прямой (а1), проходящей через точку М0 (2, 1), параллельно данной прямой. 2) Составить уравнение прямой (а2), проходящей через точку М0 (2, 1), перпендикулярно данной прямой.
. 1) Составить уравнение прямой (а1), проходящей через точку М0 (2, 1), параллельно данной прямой. 2) Составить уравнение прямой (а2), проходящей через точку М0 (2, 1), перпендикулярно данной прямой.
Решение.
1) 1 способ. Найдем угловой коэффициент прямой (а): 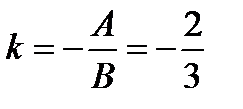 . Условие параллельности двух прямых:
. Условие параллельности двух прямых: 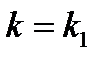 , то есть угловой коэффициент прямой (а1):
, то есть угловой коэффициент прямой (а1): 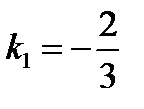 . Подставим в уравнение (3):
. Подставим в уравнение (3): 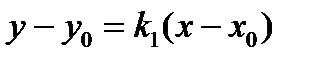 и получим
и получим  . Отсюда общее уравнение прямой (а1) имеет вид:
. Отсюда общее уравнение прямой (а1) имеет вид:
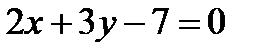 .
.
2 способ. Нормальный вектор 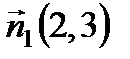 Прямые параллельны, следовательно, параллельны их нормальные вектора. То есть нормальный вектор прямой (а1):
Прямые параллельны, следовательно, параллельны их нормальные вектора. То есть нормальный вектор прямой (а1): 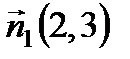 . Подставим в уравнение (2):
. Подставим в уравнение (2): 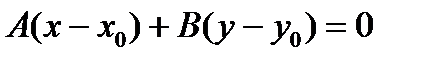 и получим
и получим  . Отсюда общее уравнение прямой (а1) имеет вид:
. Отсюда общее уравнение прямой (а1) имеет вид: 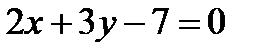 .
.
2) 1 способ. Найдем угловой коэффициент прямой (а): 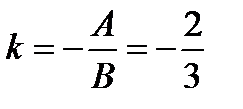 . Условие перпендикулярности двух прямых:
. Условие перпендикулярности двух прямых: 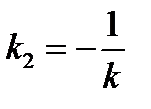 , то есть угловой коэффициент прямой (а2):
, то есть угловой коэффициент прямой (а2): 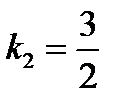 . Подставим в уравнение (3):
. Подставим в уравнение (3): 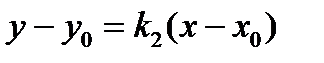 и получим
и получим  . Отсюда общее уравнение прямой (а1) имеет вид:
. Отсюда общее уравнение прямой (а1) имеет вид:  .
.
2 способ. Нормальный вектор 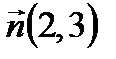 Прямые перпендикулярны, следовательно, нормальный вектор прямой (а) параллелен прямой (а2), то есть является направляющим вектором прямой (а2):
Прямые перпендикулярны, следовательно, нормальный вектор прямой (а) параллелен прямой (а2), то есть является направляющим вектором прямой (а2):  . Подставим в уравнение (4):
. Подставим в уравнение (4): 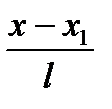
 и получим
и получим 
 ,. Отсюда общее уравнение прямой (а2) имеет вид:
,. Отсюда общее уравнение прямой (а2) имеет вид:  .
.
Пример 2. Найти расстояние от прямой (АВ), где А(7, 4), В(3, –3) до точки С(5, 9).
Решение. Найдем общее уравнение прямой. Для этого подставим исходные данные в формулу (4):  и получим
и получим 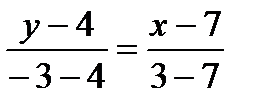 . Отсюда общее уравнение (АВ)
. Отсюда общее уравнение (АВ) 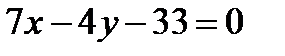 . По формуле (9)
. По формуле (9) 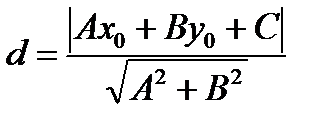 найдем искомое расстояние:
найдем искомое расстояние:  .
.
Окружность
Определение. Окружностью называется геометрическое место точек плоскости, равноудаленных от фиксированной точки, называемой центром окружности.
Теорема. Окружность радиуса R с центром в точке  имеет уравнение
имеет уравнение
| |
|
 Любое уравнение окружности с помощью тождественных преобразований можно привести к каноническому виду (1). Для этого достаточно выделить полные квадраты по переменным
Любое уравнение окружности с помощью тождественных преобразований можно привести к каноническому виду (1). Для этого достаточно выделить полные квадраты по переменным 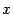 и у.
и у.
Пример. Нарисуйте кривую 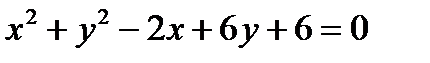 .
.
Решение. Сгруппируем 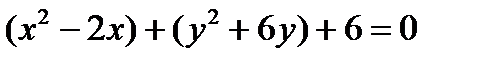 .
.
Выделим полные квадраты, получим: 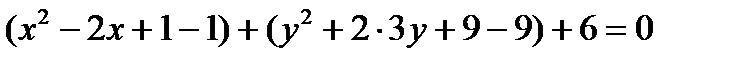 .
.
Отсюда 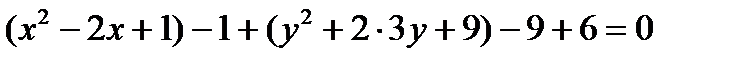 ,
,
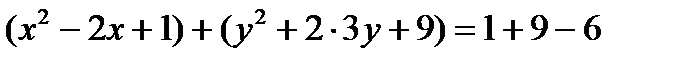 .
.
Тогда каноническое уравнение имеет вид:  .
.
Итак, центр окружности -точка М0(1,-3), радиус равен 2.
Эллипс
Определение. Эллипсом называется геометрическое место точек плоскости, для каждой из которых сумма расстояний до двух данных точек F1 и F2 той же плоскости, называемых фокусами эллипса, есть величина постоянная и равная 2а.
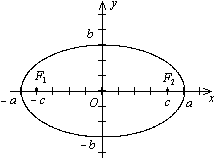 Начало О системы координат расположим на середине отрезка F1F2. Координаты фокусов F1(-с,0), F2(с,0).
Начало О системы координат расположим на середине отрезка F1F2. Координаты фокусов F1(-с,0), F2(с,0).
Тогда расстояние между фокусами равно 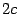 : |F1F2|=2c.
: |F1F2|=2c.
Ось 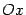 направим вдоль этого отрезка, ось Oy перпендикулярна к этому отрезку.
направим вдоль этого отрезка, ось Oy перпендикулярна к этому отрезку.
Теорема. В выбранной системе координат эллипс имеет каноническое уравнение
 (2), где
(2), где  или
или 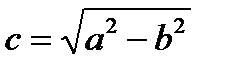
Свойства эллипса: Эллипс обладает двумя взаимно перпендикулярными осями симметрии, на одной из которых находятся его фокусы, и центром симметрии. Если эллипс задан каноническим уравнением (2), то его осями симметрии служат оси 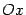 и Оу, начало координат - центр симметрии.
и Оу, начало координат - центр симметрии.
Построение эллипса. Строим две окружности с центром в точке О радиусами а и b. (a > b).Строим луч, выходящий из начала координат до пересечения с обеими окружностями. Из точек пересечения опускаем пересекающиеся лучи, параллельные координатным осям. Точка пересечения данных лучей – это очка, принадлежащая эллипсу.
Определения. Точки пересечения эллипса с его осями симметрии называются вершинами эллипса, центр симметрии - центром эллипса, отрезок между двумя вершинами, содержащий фокусы, называется большой осью эллипса, половина его длины - большой полуосью эллипса.
Если эллипс задан каноническим уравнением  , то его вершины имеют координаты (-а,0), (а,0), (0,b), (0,-b) , большая полуось равна
, то его вершины имеют координаты (-а,0), (а,0), (0,b), (0,-b) , большая полуось равна 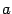 , малая полуось равна
, малая полуось равна 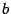 .
.
Величина  называется эксцентриситетом эллипса. Величина
называется эксцентриситетом эллипса. Величина 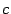 , являющаяся половиной расстояния между фокусами, определяется из формулы
, являющаяся половиной расстояния между фокусами, определяется из формулы 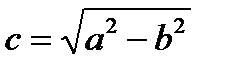 . Эксцентриситет
. Эксцентриситет  эллипса характеризует степень вытянутости эллипса. Чем ближе экcцентриситет к нулю, тем больше эллипс похож на окружность. Чем ближе эксцентриситет к 1, тем сильнее вытянут эллипс. Отметим, что по определению для эллипса
эллипса характеризует степень вытянутости эллипса. Чем ближе экcцентриситет к нулю, тем больше эллипс похож на окружность. Чем ближе эксцентриситет к 1, тем сильнее вытянут эллипс. Отметим, что по определению для эллипса 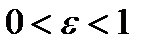 .
.
Прямые, между которыми вытянут эллипс, называются директрисами, уравнения которых 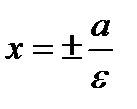 .
.
Замечание 1.Уравнение (2) было получено в предположении, что F1 и F2 - различные точки, то есть c > 0. Тогда b < a. Но кривую, определяемую уравнением, можем рассмотреть и в случае  , (c = 0). Уравнение в этом случае после умножения на
, (c = 0). Уравнение в этом случае после умножения на 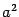 примет вид
примет вид 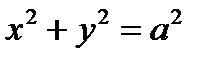 . Это уравнение окружности радиуса
. Это уравнение окружности радиуса 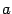 с центром в начале координат. Таким образом, можно рассматривать окружность как предельный вариант эллипса, когда
с центром в начале координат. Таким образом, можно рассматривать окружность как предельный вариант эллипса, когда 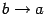 ,
, 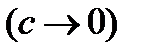 , или, как иногда говорят математики, окружность является "вырожденным" эллипсом, у которого фокусы совпали.
, или, как иногда говорят математики, окружность является "вырожденным" эллипсом, у которого фокусы совпали.
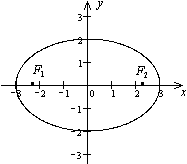 Замечание 2. Если
Замечание 2. Если  , то фокусы лежат на оси (Оу) и имеют координаты F1(0,-с), F2(0,с), где
, то фокусы лежат на оси (Оу) и имеют координаты F1(0,-с), F2(0,с), где 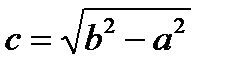 . Эксцентриситет
. Эксцентриситет  . Уравнения директрис
. Уравнения директрис 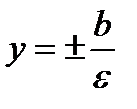
Замечание 3. Если центр эллипса лежит в точке М0(х0,у0), то каноническое уравнение эллипса примет вид: 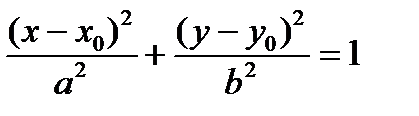 . Уравнения директрис
. Уравнения директрис 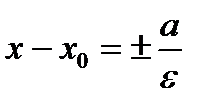 , координаты фокусов F1(х0–с, у0), F2((х0+с, у0).
, координаты фокусов F1(х0–с, у0), F2((х0+с, у0).
Пример 1. Постройте кривую 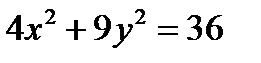 . Найдите фокусы и эксцентриситет.
. Найдите фокусы и эксцентриситет.
Решение. Разделим обе части уравнения на 36. Получаем уравнение 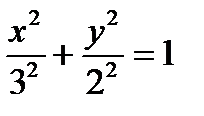 . Это каноническое уравнение эллипса,
. Это каноническое уравнение эллипса,  ,
, 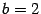 . Из соотношения находим
. Из соотношения находим 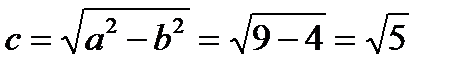 , фокусы F1(
, фокусы F1( 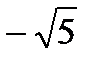 , 0), F2(
, 0), F2(  , 0), эксцентриситет
, 0), эксцентриситет 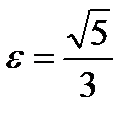 .
.
Пример 2. Найдите фокусы и эксцентриситет эллипса  .
.
Решение. Уравнение запишем в виде 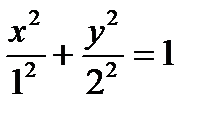 , где
, где 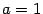 ,
, 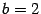 , b > a. Отсюда
, b > a. Отсюда 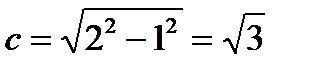 . Фокусы имеют координаты F1(
. Фокусы имеют координаты F1( 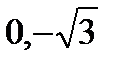 ), F2(
), F2( 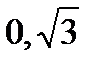 ). Эксцентриситет равен
). Эксцентриситет равен  .
.
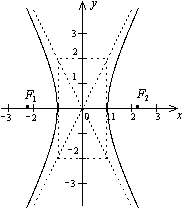
Гипербола .
Из школьного курса математики известно, что кривая, задаваемая уравнением  , где
, где  – число, называется гиперболой. Однако это - частный случай гиперболы (равносторонняя гипербола).
– число, называется гиперболой. Однако это - частный случай гиперболы (равносторонняя гипербола).
Определение. Гиперболой называется геометрическое место точек плоскости, для каждой из которых абсолютная величина разности расстояний до двух фиксированных точек F1 и F2 той же плоскости, называемых фокусами гиперболы, есть величина постоянная равная 2а.
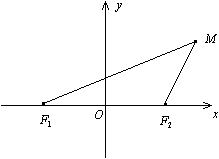
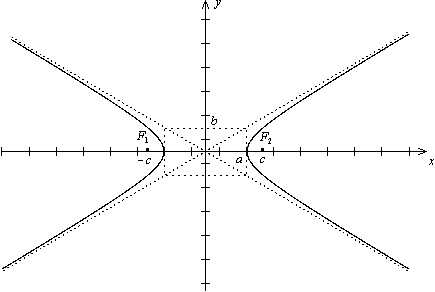 Теорема. Пусть расстояние между фокусами гиперболы равно
Теорема. Пусть расстояние между фокусами гиперболы равно 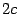 , т.е. фокусы имеют координаты F1(-с,0), F2(с,0), тогда в выбранной системе координат гипербола имеет уравнение
, т.е. фокусы имеют координаты F1(-с,0), F2(с,0), тогда в выбранной системе координат гипербола имеет уравнение  (3), где
(3), где  или
или 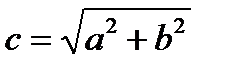 .
.
Свойство. Гипербола обладает двумя взаимно перпендикулярными осями симметрии, на одной из которых лежат фокусы гиперболы, и центром симметрии. Если гипербола задана каноническим уравнением (3), то ее осями симметрии служат координатные оси 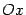 и Оу, а начало координат - центр симметрии гиперболы.
и Оу, а начало координат - центр симметрии гиперболы.
Определения. Точки пересечения гиперболы, заданной каноническим уравнением (3), с осью 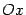 называются вершинами гиперболы, отрезок между ними называется действительной осью гиперболы. Отрезок оси ординат между точками (0, -b) и (0,b) называется мнимой осью. Числа
называются вершинами гиперболы, отрезок между ними называется действительной осью гиперболы. Отрезок оси ординат между точками (0, -b) и (0,b) называется мнимой осью. Числа 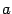 и
и 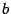 называются соответственно действительной и мнимой полуосями гиперболы. Начало координат называется ее центром.
называются соответственно действительной и мнимой полуосями гиперболы. Начало координат называется ее центром.
Величина  называется эксцентриситетом гиперболы. Величина с > a, то есть у гиперболы
называется эксцентриситетом гиперболы. Величина с > a, то есть у гиперболы 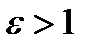 . Эксцентриситет
. Эксцентриситет  характеризует угол между асимптотами, чем ближе
характеризует угол между асимптотами, чем ближе  к 1, тем меньше этот угол.
к 1, тем меньше этот угол.
Прямые  , к которым график гиперболы приближается, но не пересекает, называются асимптотами гиперболы. Уравнения директрис
, к которым график гиперболы приближается, но не пересекает, называются асимптотами гиперболы. Уравнения директрис 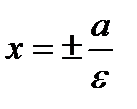 .
.
Построение гиперболы. Чертим основной прямоугольник, т.е. прямоугольник с центром в начале координат со сторонами 2a и 2b, диагоналями которого будут асимптотами гиперболы (см. рис. выше в определении).
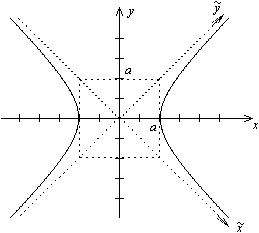 Замечание 1. В отличие от эллипса в каноническом уравнении гиперболы соотношение между величинами
Замечание 1. В отличие от эллипса в каноническом уравнении гиперболы соотношение между величинами  и
и 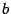 может быть произвольным. В частности, при
может быть произвольным. В частности, при  мы получим равностороннюю гиперболу, известную из школьного курса математики. Ее уравнение имеет знакомый вид
мы получим равностороннюю гиперболу, известную из школьного курса математики. Ее уравнение имеет знакомый вид 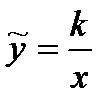 , если взять
, если взять  , а оси
, а оси 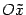 и
и  направить по биссектрисам четвертого и первого координатных углов (рис.).
направить по биссектрисам четвертого и первого координатных углов (рис.).
Замечание 2. Если каноническое уравнение гиперболы имеет вид  (3*), то ее фокусы располагаются на оси Оу, их координаты F1(0,-с), F2(0,с), числа
(3*), то ее фокусы располагаются на оси Оу, их координаты F1(0,-с), F2(0,с), числа 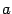 и
и 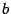 называются соответственно мнимой и действительной полуосями гиперболы; уравнения асимптот
называются соответственно мнимой и действительной полуосями гиперболы; уравнения асимптот 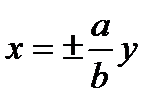 , уравнения директрис
, уравнения директрис  . (См. рис. примера 2)
. (См. рис. примера 2)
Вообще говоря, данное уравнение (3*) не является каноническим, так как знаки перед 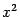 и у2 противоположны знакам в первом каноническом уравнении (3). Но, если переобозначить переменные, т.е. взять
и у2 противоположны знакам в первом каноническом уравнении (3). Но, если переобозначить переменные, т.е. взять 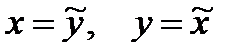 , то получим снова каноническое уравнение (3):
, то получим снова каноническое уравнение (3): 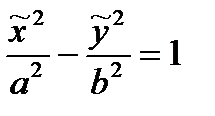 . В связи с этим уравнение (3*) будем сразу называть каноническим.
. В связи с этим уравнение (3*) будем сразу называть каноническим.
 Замечание 3. Если центр гиперболы смещен и лежит в точке М0(х0,у0), то каноническое уравнение гиперболы примет вид:
Замечание 3. Если центр гиперболы смещен и лежит в точке М0(х0,у0), то каноническое уравнение гиперболы примет вид:  (или
(или 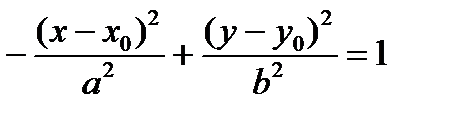 ). Тогда координаты фокусов F1(х0-с, у0), F2(х0+с, у0), уравнения асимптот
). Тогда координаты фокусов F1(х0-с, у0), F2(х0+с, у0), уравнения асимптот 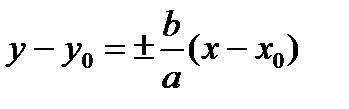 , уравнения директрис
, уравнения директрис 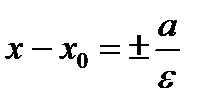 .
.
Пример 1. Постройте гиперболу 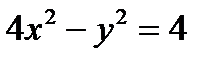 , найдите ее фокусы и эксцентриситет.
, найдите ее фокусы и эксцентриситет.
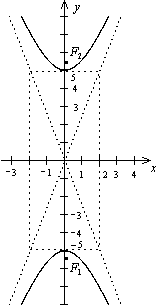 Решение. Разделим обе части уравнения на 4. Получим каноническое уравнение
Решение. Разделим обе части уравнения на 4. Получим каноническое уравнение  ,
, 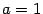 ,
, 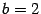 . Проводим асимптоты
. Проводим асимптоты 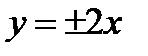 и строим гиперболу. Из формулы получим
и строим гиперболу. Из формулы получим 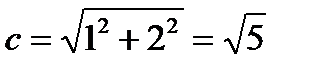 . Тогда фокусы
. Тогда фокусы  , эксцентриситет
, эксцентриситет 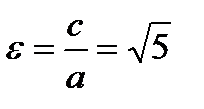 .
.
Пример 2. Постройте гиперболу 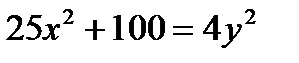 . Найдите ее фокусы и эксцентриситет.
. Найдите ее фокусы и эксцентриситет.
Решение. Преобразуем уравнение к виду 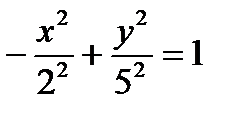 . Фокусы гиперболы лежат на оси (Оу), действительная полуось b = 5, мнимая а = 2. Асимптоты имеют уравнение
. Фокусы гиперболы лежат на оси (Оу), действительная полуось b = 5, мнимая а = 2. Асимптоты имеют уравнение 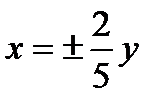 . Из формулы получим
. Из формулы получим 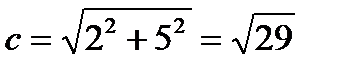 , эксцентриситет
, эксцентриситет 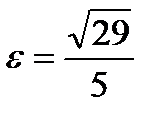 , координаты фокусов
, координаты фокусов 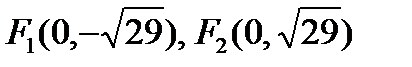 .
.
Парабола
В школьном курсе математики достаточно подробно изучалась парабола, которая, по определению, являлась графиком квадратного трехчлена. Здесь мы дадим другое (геометрическое) определение параболы.
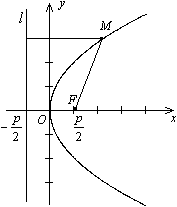 Определение. Параболой называется геометрическое место точек плоскости, для каждой из которых расстояние до фиксированной точки F этой плоскости, называемой фокусом, равно расстоянию до фиксированной прямой, лежащей в той же плоскости и называемой директрисой параболы.
Определение. Параболой называется геометрическое место точек плоскости, для каждой из которых расстояние до фиксированной точки F этой плоскости, называемой фокусом, равно расстоянию до фиксированной прямой, лежащей в той же плоскости и называемой директрисой параболы.
Чтобы получить уравнение кривой, соответствующей этому определению, введем подходящую систему координат. Пусть расстояние между фокусом 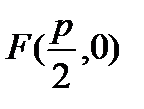 и директрисой параболы l, уравнение которой
и директрисой параболы l, уравнение которой 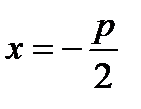 , равно p (
, равно p ( 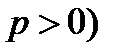 .
.
Теорема. В выбранной системе координат парабола имеет уравнение 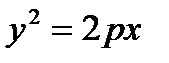 . (4)
. (4)
Уравнение (4) называется каноническим уравнением параболы.
Замечание. Парабола обладает осью симметрии. Если парабола задана каноническим уравнением, то ось симметрии совпадает с осью 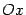 . Асимптот парабола не имеет.
. Асимптот парабола не имеет.
Определение. Точка пересечения оси симметрии с параболой называется вершиной параболы.

Построение. Проведем прямую 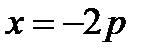 . Выберем на ней произвольным образом точку М. Проведем через точку М луч (ОМ) и луч, параллельный оси Ох. Проведем луч, выходящий из начала координат перпендикулярно лучу (ОМ) до пересечения с лучом, параллельным оси Ох. Точка их пересечения принадлежит параболе.
. Выберем на ней произвольным образом точку М. Проведем через точку М луч (ОМ) и луч, параллельный оси Ох. Проведем луч, выходящий из начала координат перпендикулярно лучу (ОМ) до пересечения с лучом, параллельным оси Ох. Точка их пересечения принадлежит параболе.
Пара пересекающихся прямых
Канонические уравнения: 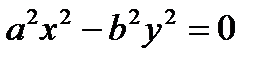 ,
, 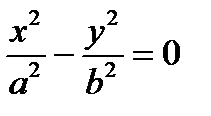 . (5)
. (5)
Применим формулу - разность квадратов: 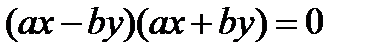 , следовательно,
, следовательно, 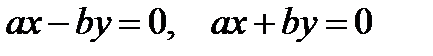 . Отсюда
. Отсюда 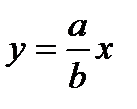 и
и 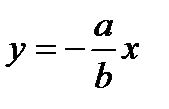 - пара пересекающихся в точке О(0, 0) прямых.
- пара пересекающихся в точке О(0, 0) прямых.
Аналогично получаем во втором случае пара пересекающихся в точке О(0, 0) прямых  и
и 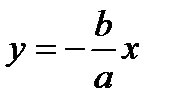 .
.
Замечание. Если прямые пересекаются в точке М0(х0, у0), то уравнения имеют вид 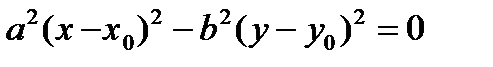 и
и 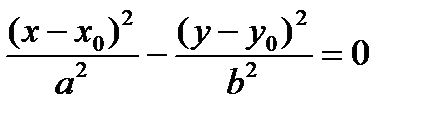 .
.
Пример на нахождение канонического уравнения.
Пример. Найти каноническое уравнение кривой 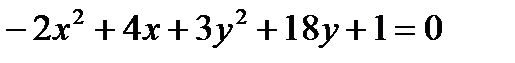 .
.
Решение. Группируем. Выносим за скобки множители, стоящие перед квадратами.

Выделяем полные квадраты в скобках согласно формуле: 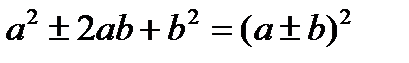
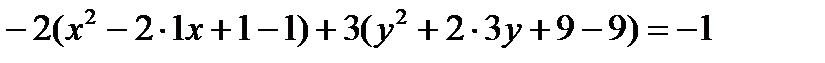
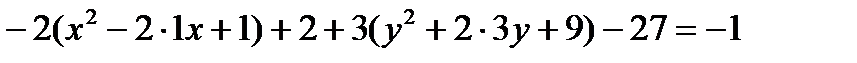

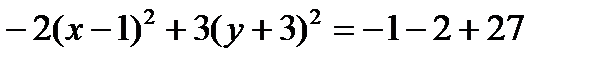
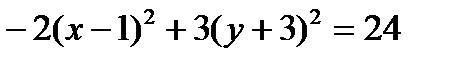
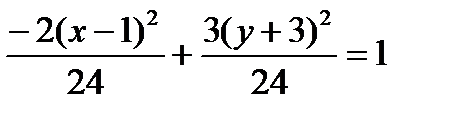
В числителе перед скобками должны стоять единицы:
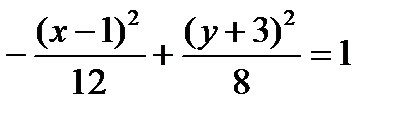 - каноническое уравнение гиперболы с центром в точке
- каноническое уравнение гиперболы с центром в точке 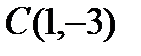 , полуоси которой равны
, полуоси которой равны 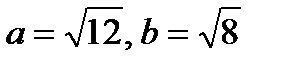 , директрисы параллельны оси (Ох) (ветви вытянуты вдоль (Ох)).
, директрисы параллельны оси (Ох) (ветви вытянуты вдоль (Ох)).
П. 4. Уравнение плоскости
| α |

|
| М |
| М0 |
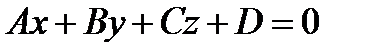 (1)
(1)
Координаты нормального вектора:  ,
, 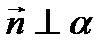 .
.
Уравнение плоскости, проходящей через данную точку 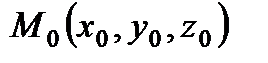 , перпендикулярно заданному вектору
, перпендикулярно заданному вектору  :
:
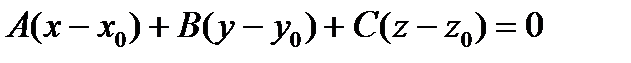 (2).
(2).
Вывод: Рассмотрим текущую точку плоскости 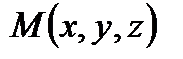 и рассмотрим вектор
и рассмотрим вектор 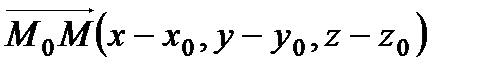 , который будет лежать в плоскости α. Нормальный вектор
, который будет лежать в плоскости α. Нормальный вектор  перпендикулярен плоскости α, следовательно, векторы
перпендикулярен плоскости α, следовательно, векторы 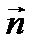 и
и  перпендикулярны. Условие перпендикулярности векторов – равенство нулю их скалярного произведения:
перпендикулярны. Условие перпендикулярности векторов – равенство нулю их скалярного произведения: 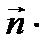
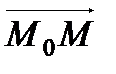 =0, то есть
=0, то есть
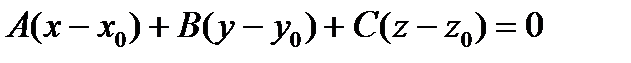 .
.
Замечание. Раскрыв скобки в уравнении (2), получим уравнение (1).
Уравнение плоскости в отрезках 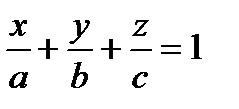 , (3)
, (3)
где a, b, c – величины отрезков, отсекаемых плоскостью от координатных осей.
П. 5. Прямая в пространстве
Рассмотрим в пространстве R3 прямую (а), проходящую через данную точку  , параллельно заданному вектору
, параллельно заданному вектору 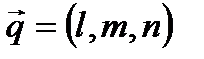 .
. 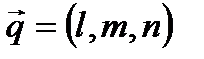 – направляющий вектор прямой.
– направляющий вектор прямой.
| М |
| М0 |
|
| а |
Вывод уравнения (а): Рассмотрим текущую точку прямой 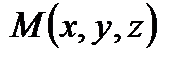 и рассмотрим вектор
и рассмотрим вектор 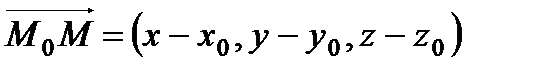 , который будет лежать на прямой (а). Направляющий вектор прямой
, который будет лежать на прямой (а). Направляющий вектор прямой 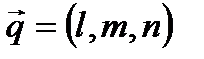 параллелен прямой (а), следовательно, векторы
параллелен прямой (а), следовательно, векторы  и
и  параллельны или коллинеарны. Условие коллинеарности двух векторов – пропорциональность их координат:
параллельны или коллинеарны. Условие коллинеарности двух векторов – пропорциональность их координат:
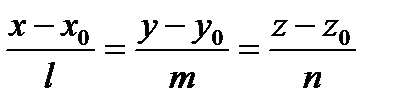 – канонические уравнения прямой. (1)
– канонические уравнения прямой. (1)
Уравнение прямой, проходящей через две заданные точки 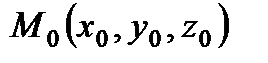 и
и 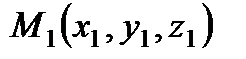
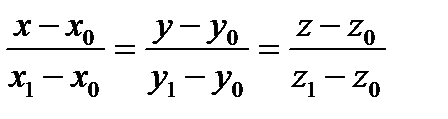 (2)
(2)
Вывод: Рассмотрим текущую точку прямой 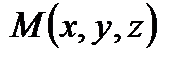 и рассмотрим векторы
и рассмотрим векторы 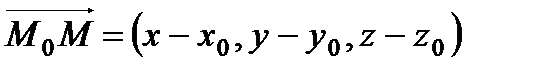 и
и  , которые будут параллельны. Условие коллинеарности двух векторов – пропорциональность их координат.
, которые будут параллельны. Условие коллинеарности двух векторов – пропорциональность их координат.
Приравняем уравнение (2) к параметру t: 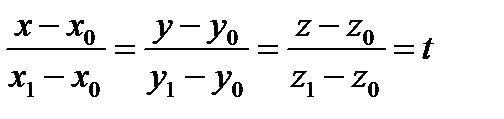 , отсюда
, отсюда
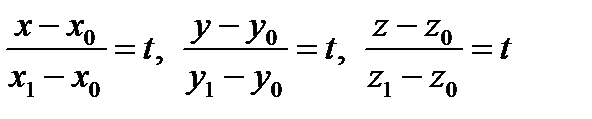 или
или  – параметрическое уравнение прямой (3)
– параметрическое уравнение прямой (3)
Множество точек пересечения двух различных плоскостей α1 и α2, имеющих общую точку:
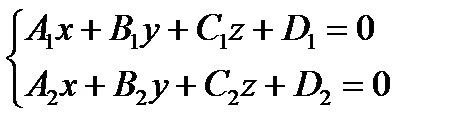 – общее уравнение прямой (4).
– общее уравнение прямой (4).
Направляющий вектор данной прямой находится как 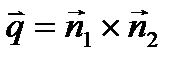 , координаты точки M0(x0, y0 z0), лежащей на прямой, удовлетворяют системе уравнений (4).
, координаты точки M0(x0, y0 z0), лежащей на прямой, удовлетворяют системе уравнений (4).
Примеры.
 α α
|
| М0 |
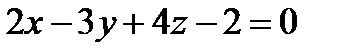 , проходящей через точку М0(0, 0, 1/2).
, проходящей через точку М0(0, 0, 1/2).
|
| α |
Нормальный вектор плоскости коллинеарен направляющему вектору
прямой 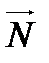
 . Следовательно, координаты направляющего
. Следовательно, координаты направляющего
вектора прямой пропорциональны (совпадают) с координатами нормального вектора.
Подставим данные в каноническое уравнение: Ответ: 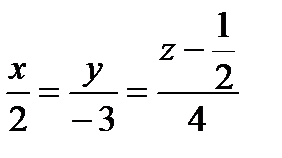
Задача 2. Найти точку пересечения прямой  и плоскости
и плоскости 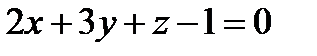 .
.
Решение.
Координаты точки пересечения М – это решение системы  .
.
| α |
| М |
 , отсюда
, отсюда 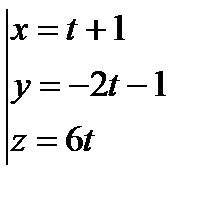 .
.
Найдем решение системы:
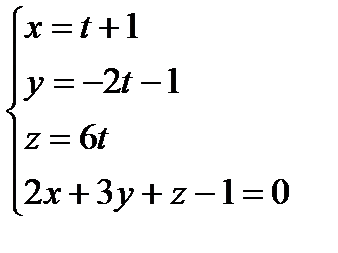
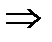
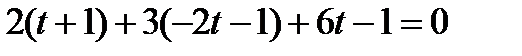
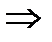
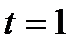 ,
,
отсюда х = 1+1=2, у = -2 - 1= -3, z = 6 – координаты точки пересечения. Ответ: 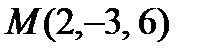 .
.
Задача 3. Найти угол 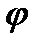 между прямой в:
между прямой в: 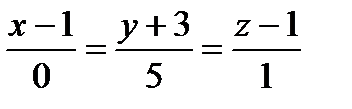 и плоскостью
и плоскостью  :
: 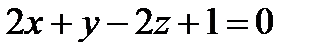 .
.
Решение.
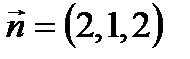 ,
,  . Угол между прямой и плоскостью находится по формуле:
. Угол между прямой и плоскостью находится по формуле:
 .
.
Задача 4. Написать уравнение проекции прямой l: 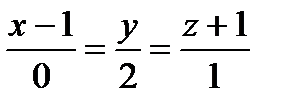 на плоскость
на плоскость  :
: 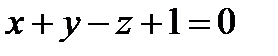 .
.
Решение.
 α α
|

|
 ,
, 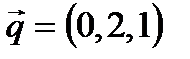 .
.
| α1 |
| А |
 ,
,
| l |
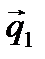 А А
|
 .
. | α |
| d |
Пересечение полученной плоскости с плоскостью  -
-
прямая d - и будет искомой проекцией.
Уравнение плоскости 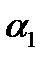 , походящей через прямую l перпендикулярно плоскости
, походящей через прямую l перпендикулярно плоскости  можно найти либо 1 методом, либо 2-ым. Это уравнение имеет вид:
можно найти либо 1 методом, либо 2-ым. Это уравнение имеет вид:  . Нормальный вектор
. Нормальный вектор 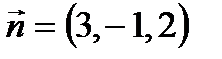 .
.
Тогда общее уравнение искомой прямой d имеет вид: 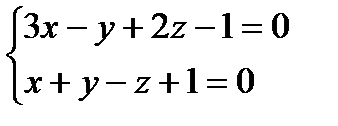 .
.
Запишем это уравнение в каноническом виде. Для этого необходимо найти точку А, лежащую на прямой, и направляющий вектор 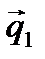 .
.
Найдем координаты точки А: пусть z = 0, тогда 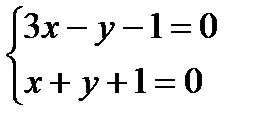 , методом Гаусса получим, что
, методом Гаусса получим, что
х = 0, у =-1. Координаты точки А(0, -1, 0).
Направляющий вектор  найдем по формуле:
найдем по формуле: 
Уравнение прямой d – уравнение искомой проекции имеет вид:  .
.
Вывод.
Определение. Сфера – геометрическое место точек, расстояние от которых до данной точки М0(х0, у0, z0) – центра есть величина постоянная и равная R.
Рассмотрим текущую точку сферы М(х, у, z). Тогда 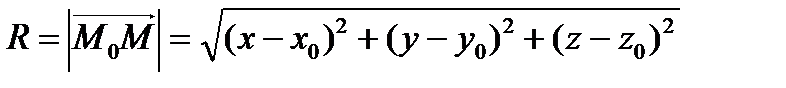 . Отсюда
. Отсюда  – каноническое уравнение сферы с центром в точке М0(х0, у0, z0) и радиусом R.
– каноническое уравнение сферы с центром в точке М0(х0, у0, z0) и радиусом R.
Цилиндрические поверхности
Пусть в общем уравнении поверхности отсутствует одна координата, например z, т.е. уравнение имеет вид:  . Тогда вместе с точкой М0(х0, у0, z0), лежащей на поверхности, на ней будет лежать и прямая, параллельная оси (О z) и проходящая через точку М1(х0, у0, 0).
. Тогда вместе с точкой М0(х0, у0, z0), лежащей на поверхности, на ней будет лежать и прямая, параллельная оси (О z) и проходящая через точку М1(х0, у0, 0).
Определение. Уравнение  называется уравнением направляющей, которой является кривая второго порядка. Прямые, проходящие через точки кривой, параллельно оси (О z), называются образующими.
называется уравнением направляющей, которой является кривая второго порядка. Прямые, проходящие через точки кривой, параллельно оси (О z), называются образующими.
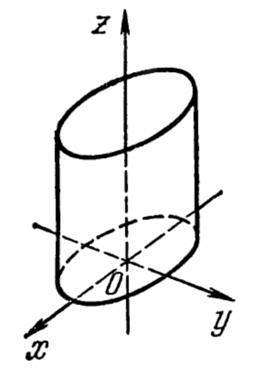
Определение. Цилиндрической поверхностью или цилиндром называется поверхность, в общем уравнении которой отсутствует одна координата:  или
или  или
или 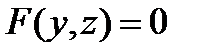 .
.
| х |
| у |
| z |
| а |
| b |
1). Эллиптические цилиндры.
а) 
В уравнении поверхности отсутствует координата z, следовательно,
образующие параллельны оси (О z), направляющая – эллипс
в плоскости (Оху) с центром в точке О.
b) 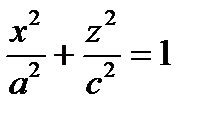
В уравнении поверхности отсутствует координата у, следовательно, образующие
параллельны оси (Оу), направляющая – эллипс в плоскости (Ох z) с центром в точке О.
с) 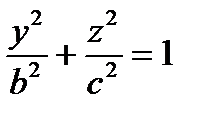
В уравнении поверхности отсутствует координата х, следовательно, образующие
параллельны оси (Ох), направляющая – эллипс в плоскости (Оу z) с центром в точке О.
| х |
| у |
| z |
| а |
 .
.
2). Гиперболические цилиндры.
а) 
В уравнении поверхности отсутствует координата z, следовательно, образующие параллельны оси (О z), направляющая – гипербола в плоскости (Оху) с центром в точке О.
b) 
В уравнении поверхности отсутствует координата у, следовательно, образующие
параллельны оси (Оу), направляющая – гипербола в плоскости (Ох z) с центром в точке О.
с) 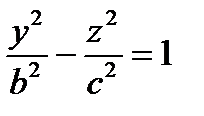
В уравнении поверхности отсутствует координата х, следовательно, образующие параллельны оси (Ох), направляющая – гипербола в плоскости (Оу z) с центром в точке О.
d)  , e)
, e) 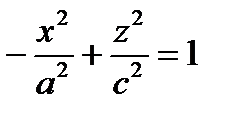 , g)
, g) 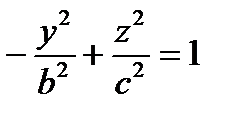
Замечание. Уравнение гиперболического цилиндра, вытянутого вдоль оси (О z) с направляющей с центром в точке М1(х0, у0, 0) имеет вид: 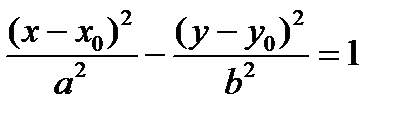 .
.
| х |
| у |
| z |
а ) 
В уравнении поверхности отсутствует координата z,
следовательно, образующие параллельны оси (О z),
направляющая – парабола в плоскости (Оху) с вершиной в точке О.
b) 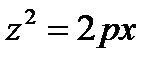
В уравнении поверхности отсутствует координата у,
следовательно, образующие параллельны оси (Оу),
направляющая – парабола в плоскости (Ох z) с вершиной в точке О.
с) 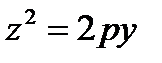
В уравнении поверхности отсутствует координата х, следовательно, образующие
параллельны оси (Ох), направляющая – парабола в плоскости (Оу z) с вершиной в точке О.
d) 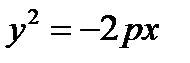 , e)
, e)  , g)
, g)  , f)
, f)  , h)
, h) 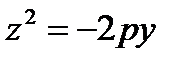 , k)
, k)  .
.
Замечание. Уравнение параболического цилиндра, вытянутого вдоль оси (О z) с направляющей – параболой, симметричной оси (Ох) и с вершиной в точке М1(х0, у0, 0) имеет вид: 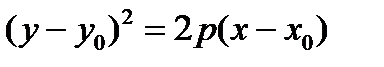 .
.
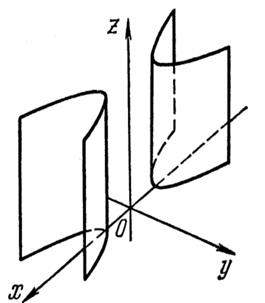

Конические поверхности
Определение. Конической поверхностью или конусом называется поверхность, образованная точками прямых, проходящих через данную точку – вершину и пересекающих данную прямую направляющую.
Канонические уравнения конуса: 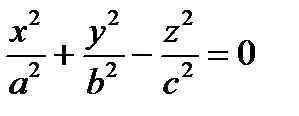 ,
, 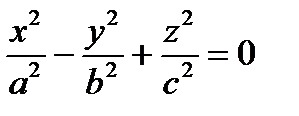 ,
, 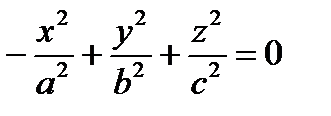 .
.
Перед какой переменной стоит знак «–», вдоль той оси вытянут конус.
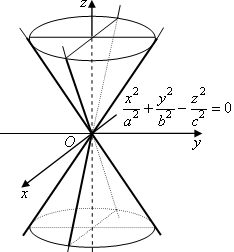
Исследуем форму конуса, заданного уравнением 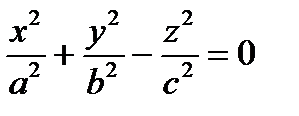 методом сечений.
методом сечений.
Метод сечений заключается в том, что поверхность пересекают плоскостями, параллельными координатным плоскостям, и изучают линии, получающиеся при пересечении.
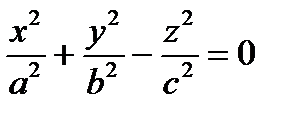 .
.
1)  , удобнее брать h = 0, т.е.
, удобнее брать h = 0, т.е.  две пересекающиеся прямые в точке О в плоскости (О yz).
две пересекающиеся прямые в точке О в плоскости (О yz).
2) 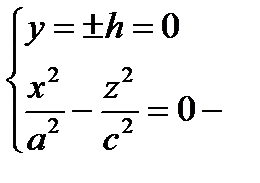 две пересекающиеся прямые в точке О в плоскости (Oxz)
две пересекающиеся прямые в точке О в плоскости (Oxz)
3) 

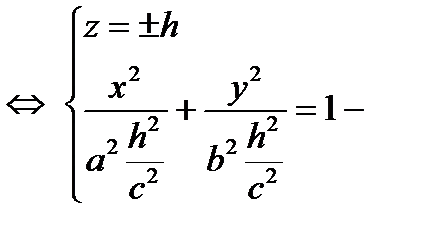 уравнение эллипса в плоскостях, параллельных плоскости (Оху)
уравнение эллипса в плоскостях, параллельных плоскости (Оху)
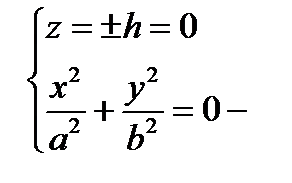 точка О.
точка О.
| х |
| у |
| z |
| О |
| h |
| - h |
Построение.
Замечание. Уравнение конуса, вытянутого вдоль оси (О z) с вершиной в точке М0(х0, у0, z0) имеет вид:  .
.
Эллипсоид.
 – каноническое уравнение эллипсоида.
– каноническое уравнение эллипсоида.

Исследуем его форму методом сечений.
1)  , удобнее брать h = 0, т.е.
, удобнее брать h = 0, т.е. 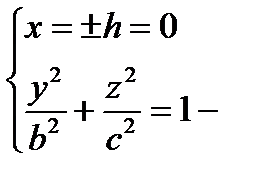 эллипс в плоскости (Oyz)
эллипс в плоскости (Oyz)
2)  эллипс в плоскости (Oх z)
эллипс в плоскости (Oх z)
3) 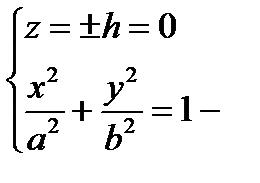 эллипс в плоскости (Oх y)
эллипс в плоскости (Oх y)
Замечание. Уравнение эллипсоида с центром в точке М0(х0, у0, z0) имеет вид:  .
.
Гиперболоиды
Однополостный гиперболоид
 ,
, 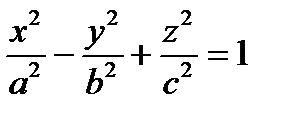 ,
, 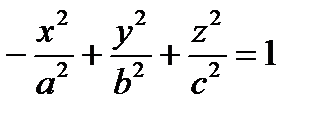 – канонические уравнения однополостного гиперболоида.
– канонические уравнения однополостного гиперболоида.
Перед какой переменной стоит знак «–», вдоль той оси вытянут гиперболоид.
Исследуем форму однополостного гиперболоида, заданного уравнением  , методом сечений.
, методом сечений.
1) 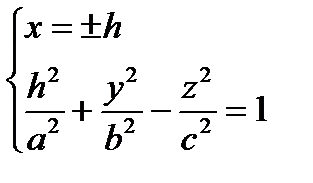 , удобнее брать h = 0, т.е.
, удобнее брать h = 0, т.е.  гипербола в плоскости (Oyz), ветви симметричны (О z)
гипербола в плоскости (Oyz), ветви симметричны (О z)
2) 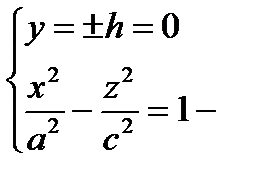 гипербола в плоскости (Oх z), ветви симметричны (О z)
гипербола в плоскости (Oх z), ветви симметричны (О z)
3) 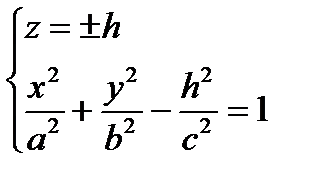
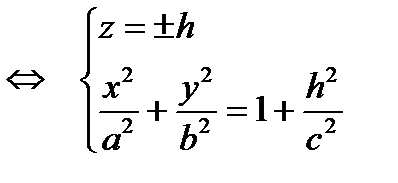
 эллипсы, лежащие в плоскостях, параллельных плоскости (Оху)
эллипсы, лежащие в плоскостях, параллельных плоскости (Оху)
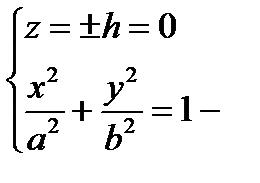 эллипс в плоскости (Oх y).
эллипс в плоскости (Oх y).
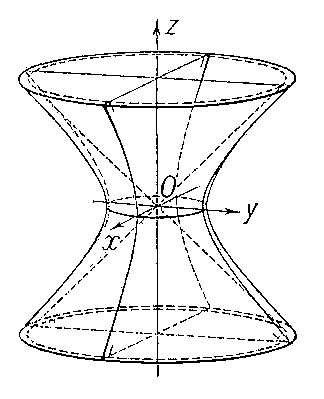
Замечание. Уравнение однополостного гиперболоида с центром в точке М0(х0, у0, z0), вытянутого вдоль оси (Oz), имеет вид: 
Двуполостный гиперболоид
 ,
, 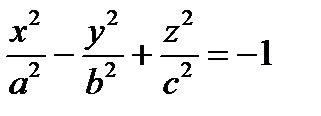 ,
, 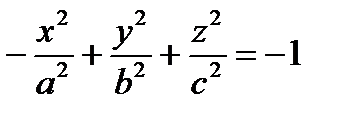 – канонические уравнения двуполостного гиперболоида.
– канонические уравнения двуполостного гиперболоида.
Перед какой переменной стоит знак «–», на той оси вытянут гиперболоид.
Исследуем форму двуполостного гиперболоида, заданного уравнением 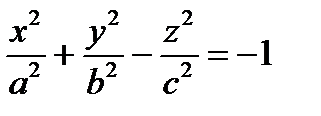 , методом сечений.
, методом сечений.
1) 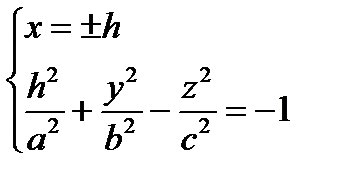 , удобнее брать h = 0, т.е.
, удобнее брать h = 0, т.е. 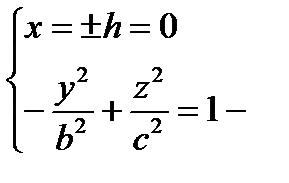 гипербола в плоскости (Oyz), ветви симметричны (Оу)
гипербола в плоскости (Oyz), ветви симметричны (Оу)
2)  гипербола в плоскости (Oх z), ветви симметричны (Ох)
гипербола в плоскости (Oх z), ветви симметричны (Ох)
3) 
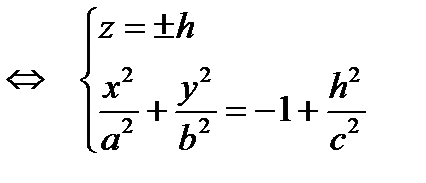
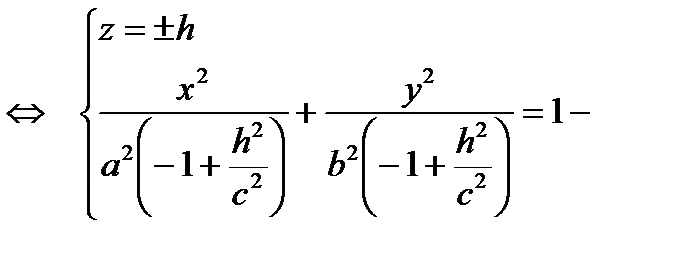 эллипсы, лежащие в плоскостях, параллельных плоскости (Оху)
эллипсы, лежащие в плоскостях, параллельных плоскости (Оху)
Очевидно, что должно выполняться неравенство: 
Значение z = 0 не может быть. 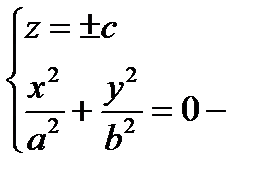 точки с координатами в (0, 0, ±с).
точки с координатами в (0, 0, ±с).

Замечание. Уравнение двуполостного гиперболоида с центром в точке М0(х0, у0, z0), расположенного вдоль оси (Oz), имеет вид:  .
.
Параболоиды
Эллиптический параболоид
 ,
, 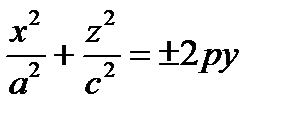 ,
,  – канонические уравнения эллиптического параболоида.
– канонические уравнения эллиптического параболоида.
Какая переменная стоит в первой степени – вдоль той оси вытянут параболоид, знак «+» или «–» показывает направление.
Исследуем форму эллиптического параболоида, заданного уравнением 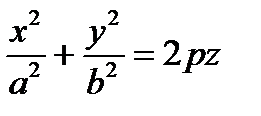 , методом сечений.
, методом сечений.
1)  , удобнее брать h = 0, т.е.
, удобнее брать h = 0, т.е. 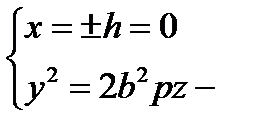 парабола с вершиной в точке О вдоль оси z в плоскости (Oyz) (ветви вверх)
парабола с вершиной в точке О вдоль оси z в плоскости (Oyz) (ветви вверх)
2) 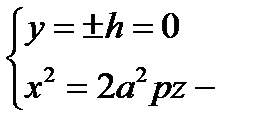 парабола с вершиной в точке О вдоль оси z в плоскости (Oх z) (ветви вверх)
парабола с вершиной в точке О вдоль оси z в плоскости (Oх z) (ветви вверх)
3) 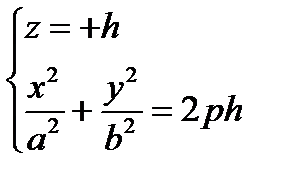
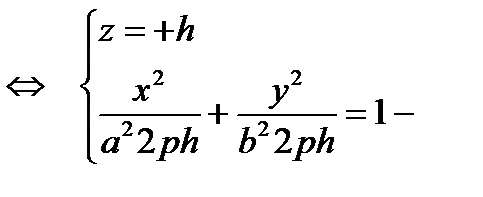 эллипсы, лежащие в плоскостях, параллельных плоскости (Oху)
эллипсы, лежащие в плоскостях, параллельных плоскости (Oху)
z = – h не может быть.
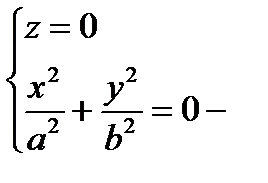 точка О.
точка О.

Замечание. Уравнение эллиптического параболоида с центром в точке М0(х0, у0, z0), расположенного вдоль оси (Oz), имеет вид:  .
.
Поверхности вращения.
Пусть в плоскости (Оу z) задана линия L, уравнение которой 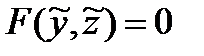 . При вращении L вокруг оси (Оу) получим некоторую поверхность (σ). Выведем уравнение этой поверхности.
. При вращении L вокруг оси (Оу) получим некоторую поверхность (σ). Выведем уравнение этой поверхности.
| х |
| у |
| z |
| О |
| М |

|
 у у
|
| L |
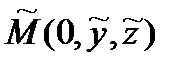 , принадлежащуюкривой L , а значит и поверхности (σ).
, принадлежащуюкривой L , а значит и поверхности (σ).
Проведем через точку  плоскость (α), перпендикулярную оси (Оу).
плоскость (α), перпендикулярную оси (Оу).
Пересечением поверхности (σ) с плоскостью (α) будет окружность с центром в точке  .
.
Рассмотрим точку М(х,у,z) – текущую точку поверхности (σ). Выберем ее так, чтобы она принадлежала плоскости (α).
Тогда радиус окружности 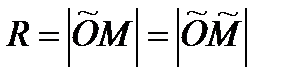 , где
, где 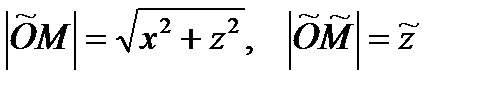 . Отсюда
. Отсюда 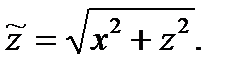 Так как
Так как  , то
, то  .
.
Уравнение поверхности (σ) найдем, подставив полученные равенства в уравнение линии L:
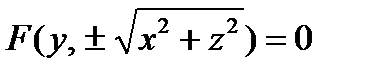 – уравнение поверхности вращения вокруг оси (Оу),
– уравнение поверхности вращения вокруг оси (Оу),
(  , так как z может быть как положительной, так и отрицательной величиной).
, так как z может быть как положительной, так и отрицательной величиной).
Аналогично выводятся уравнения поверхностей, полученных вращением линии вокруг осей (Ох) и (О z) соответственно: 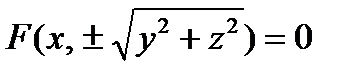 и
и 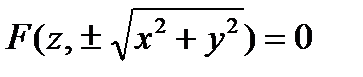 .
.
Пример.
Установить тип данной поверхности 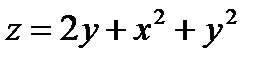 .
.
Решение.
Найдем каноническое уравнение поверхности:
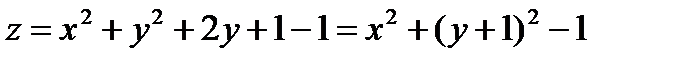 , отсюда
, отсюда 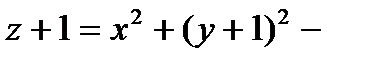 каноническое уравнение эллиптического параболоида с вершиной в точке В(0, –1, –1) (ветви парабол вверх вдоль оси (О z)).
каноническое уравнение эллиптического параболоида с вершиной в точке В(0, –1, –1) (ветви парабол вверх вдоль оси (О z)).
Матрицы
П. 1. Основные определения
Определение 1. Матрица – прямоугольная таблица, состоящая из каких-либо объектов.
Впервые появились в середине IX века в работах английских математиков У. Гамильтона и А. Кэли.
Определение 2. Числовой матрицей размерности m 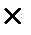 n называется таблица из (
n называется таблица из (  ) чисел, имеющая m строк и n столбцов
) чисел, имеющая m строк и n столбцов  .
.
Обозначают матрицы большими буквами.
Числа, из которых составлена матрица, называются ее элементами: aij, где i – номер строки, j – номер столбца, на пересечении которых стоит элемент aij.
Например, матрица размерности 3 на 4 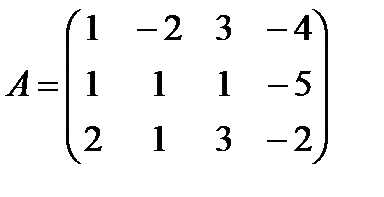 ,
, 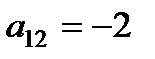 ,
,  ,
, 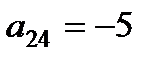 .
.
Определение 3. Матрица называется квадратной порядка n, если m = n, и прямоугольной размерности m на n, если m 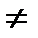 n.
n.
В примере выше матрица А – прямоугольная.
Элементы 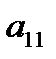 ,
,  , …,
, …, 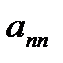 образуют главную диагональ матрицы, элементы
образуют главную диагональ матрицы, элементы 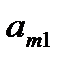 ,
,  , …,
, …, 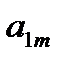 –побочную диагональ матрицы.
–побочную диагональ матрицы.
Например, у матрицы А главной диагональю является 1, 1, 3, побочной – 2, 1, 3.
Определение 4. Две матрицы называются равными, если их соответствующие элементы равны.
 , если aij = bij.
, если aij = bij.
Определение 5. Транспонированной матрицей (или сопряженной) к матрице  называется матрица
называется матрица 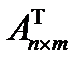 размерности n
размерности n  m, которая получается из матрицы А путем замены строк столбцами.
m, которая получается из матрицы А путем замены строк столбцами.
Например,  ,
, 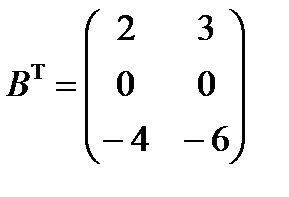 .
.
Определение 6. Квадратная матрица, у которой все элементы, не стоящие на главной диагонали, равны нулю, называется диагональной.
Определение 7. Диагональная матрица, у которой все отличные от нуля элементы, единицы, называется единичной Е.
Например,  .
.
Определение 8. Квадратная матрица называется треугольной, прямоугольная – трапециевидной, если все элементы, лежащие по одну сторону одной из ее главных диагоналей – нули.
Определение 9. Матрица, состоящая из одной строки, называется матрицей-строкой. Матрица, состоящая из одного столбца, называется матрицей-столбцом.
П. 2. Действия над матрицами
1. Матрицы одинаковой размерности можно складывать.
Определение 10. Сумой двух матриц  и
и  называется матрица
называется матрица 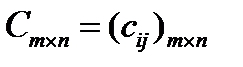 , элемент которой равен сумме соответствующих элементов матриц А и В:
, элемент которой равен сумме соответствующих элементов матриц А и В:
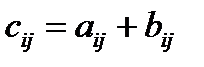 .
.
Пример. 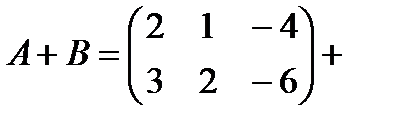

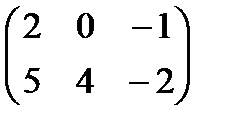 .
.
2. Определение 11. Произведением матрицы  на действительное число λ называется матрица
на действительное число λ называется матрица  , элемент которой равен произведению соответствующих элементов матрицы А на число λ:
, элемент которой равен произведению соответствующих элементов матрицы А на число λ: 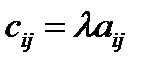 .
.
Пример. 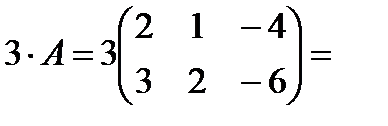
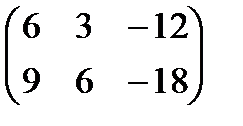
3. Определение 12. Произведением двух матриц  и
и  называется матрица
называется матрица 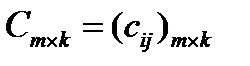 , элемент которой
, элемент которой 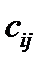 , стоящий в i-той строке и j-том столбце, равен сумме произведений соответствующих элементов i-той строки матрицы А и j-того столбца матрицы В:
, стоящий в i-той строке и j-том столбце, равен сумме произведений соответствующих элементов i-той строки матрицы А и j-того столбца матрицы В:
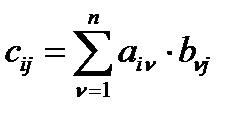 , где
, где 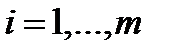 ,
, 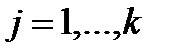 .
.
Перемножение матриц возможно лишь в том случае, когда число столбцов матрицы А равно числу строк матрицы В. Матрица С имеет столько же строк, что и матрица А, и столбцов, что и матрица В.
Пример. 
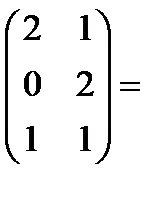 (число столбцов А равно 3, число строк В равно 3, следовательно, произведение матриц возможно) =
(число столбцов А равно 3, число строк В равно 3, следовательно, произведение матриц возможно) = 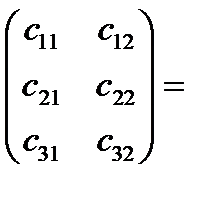
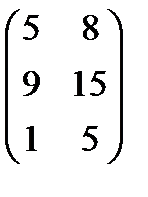
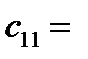 (сумма произведений элементов 1-ой строки матрицы А на соответствующие элементы 1-го столбца матрицы В) = 1·2+2·0+3·1=5,
(сумма произведений элементов 1-ой строки матрицы А на соответствующие элементы 1-го столбца матрицы В) = 1·2+2·0+3·1=5,
 (сумма произведений элементов 1-ой строки матрицы А на соответствующие элементы 2-го столбца матрицы В) = 1·1+2·2+3·1=8,
(сумма произведений элементов 1-ой строки матрицы А на соответствующие элементы 2-го столбца матрицы В) = 1·1+2·2+3·1=8,
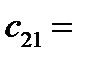 (сумма произведений элементов 2-ой строки матрицы А на соответствующие элементы 1-го столбца матрицы В) = 4·2+5·0+1·1=9,
(сумма произведений элементов 2-ой строки матрицы А на соответствующие элементы 1-го столбца матрицы В) = 4·2+5·0+1·1=9,
 (сумма произведений элементов 2-ой строки матрицы А на соответствующие элементы 2-го столбца матрицы В) = 4·1+5·2+1·1=15,
(сумма произведений элементов 2-ой строки матрицы А на соответствующие элементы 2-го столбца матрицы В) = 4·1+5·2+1·1=15,
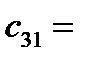 0·2+2·0+1·1=1,
0·2+2·0+1·1=1,  0·1+2·2+1·1=5.
0·1+2·2+1·1=5.
Замечания. 1) Если возможно умножение матриц А и В, то отсюда не следует возможность умножения В на А. 2) если оба произведения имеют смысл, то А·В может не совпадать с В·А.
Операции над матрицами подчиняются следующим законам:
1) А + В = В + А 2) (λ·А)·В = А(λ·В)= λ(А·В) 3) (А + В)·С =А·С+В·С 4) С ·(А + В) = С ·А+ С ·В
5) (А · В)·С =(А·В)·С 6) А·Е = А, Е·А = А. следовательно, А·Е = Е·А.
Определители
Определение 13. Определителем квадратной матрицы А называется число, которое обозначается символом  или
или 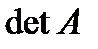 или
или 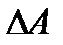 или
или  и вычисляется по некоторым правилам, в зависимости от размерности матрицы.
и вычисляется по некоторым правилам, в зависимости от размерности матрицы.
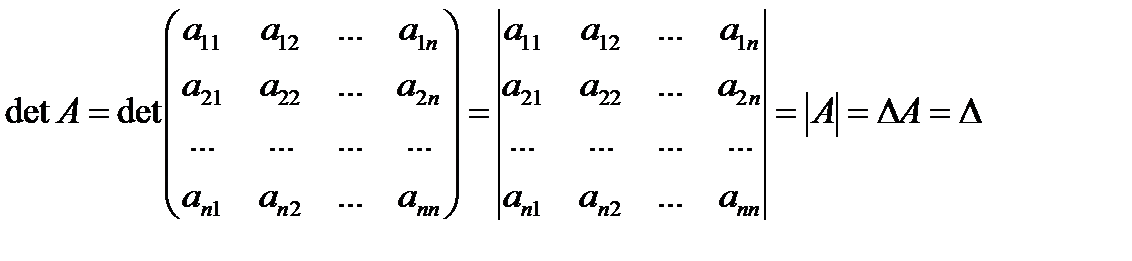
Дата: 2019-02-24, просмотров: 359.
 (1)
(1)