Диаграмма разброса (корреляция) широко применяется для выявления зависимости одних показателей (характеристик, явлений) от других [8]. На рис. 20 и 21 представлены графики зависимости параметра готового изделия A от параметров B и C комплектующих изделий. На рис. 20 наглядно прослеживается зависимость параметра A от параметра B, а из рис. 21 очевидно, что параметр A не зависит от параметра С.

Так же как и метод расслоения, корреляцию применят с целью выявления причинно–следственных связей (анализ связи причин и результата). Корреляция является прекрасным методом для "распутывания" причинно–следственных связей, но применение метода корреляции требует особой аккуратности при выполнении эксперимента. Если исследуется зависимость между двумя величинами, то говорят о парной корреляции. Когда анализируют зависимость между несколькими величинами, то речь идет о множественной корреляции (это более сложный метод анализа по сравнению с методом парной корреляции). В этом разделе будут рассмотрены некоторые основы парной корреляции. Для выявления зависимости между двумя показателями (или явлениями), например, A и B, необходимо взять выборку n и для каждой единицы продукции оценить с требуемой точностью параметры A и B. Результаты необходимо зафиксировать в контрольном листке, структуру которого следует продумать до проведения исследования (анализа). Простейшая форма контрольного листка для исследования зависимости между параметрами представлена в табл. 11.

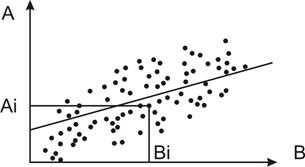
Рис. 20. График корреляционной зависимости между параметрам A и B .

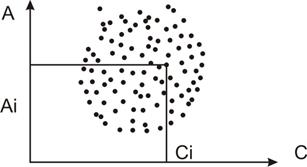
Рис. 21. График корреляционной зависимости между параметрами A и C .

Таблица 11

Контрольный листок

№ п/п	Проверяемые параметры
	A	B	C	Д
1	A1	B1	C1	Д1
2	A2	B2	C2	Д2
3	A3	B3	C3	Д3
…
	Ai	Bi	Ci	Дi
…
	An–1	Bn–1	Cn–1	Дn–1
	An	Bn	Cn	Дn
Итого n

По контрольному листку можно построить графики зависимости между: А–В; А–С; А–Д; В–С; В–Д; С–Д. Например, если по оси абсцисс отложить значение параметра В для первой детали (B₁), а по оси ординат – значение параметра А для этой же детали (A₁), то на графике получим одну точку с координатами B₁, A₁. Проделав аналогичную процедуру для всех n значений, получим на графике n точек (см. рис. 20). Следовательно, можно сделать вывод о наличия зависимости между параметрами A и B. Численно степень зависимости можно оценить величиной коэффициента корреляции r по формуле:

r= ,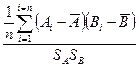

где A_i и B_i значения параметров A и B для i-й детали;

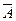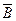,  – средние арифметические значения величин A и B;

S_A, S_B – стандартные отклонения величин А и В;

n – число изделий в выборке (объем выборки).

Рекомендуемое значение n, для выполнения корреляционного анализа: n 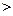30.

Коэффициент корреляции определяется по формуле:

r=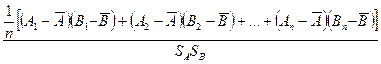

Точки, нанесенные на график в прямоугольной системе координат, образуют так называемое "поле корреляции". Если зависимость имеет место, то поле корреляции вытянуто и направление "вытянутости" не совпадает с направлением осей координат. Если величины независимы, то поле корреляции параллельно одной из осей координат или имеет форму круга (см. рис. 21). Графический анализ позволяет установить наличие зависимости и приблизительно оценить степень этой зависимости. Например, можно утверждать, что зависимость между параметрами A и Д (рис. 22) сильнее, чем между параметрами A и B (см. рис. 21) т.е. более тесная связь. Для количественной оценки такой связи между двумя величинами нужно знать коэффициент корреляции r. Причем, если r= 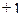, то это свидетельствует о наличии функциональной зависимости. Если r=0, то величины независимы. Чем ближе значение коэффициента корреляции к 1, тем теснее зависимость между параметрами.

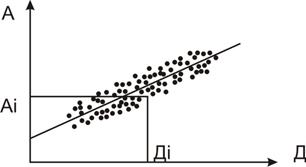
Рис. 22. График корреляционной зависимости между параметрами A и Д.

На рис. 23а изображена прямая линейная зависимость (r=+1), на рис. 23б – обратная линейная зависимость (r=-1).

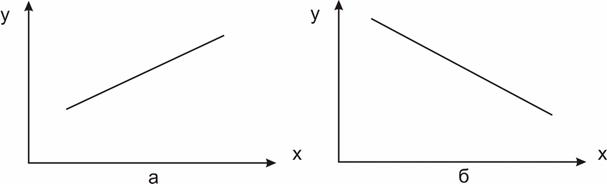
Рис. 23. Графики линейной зависимости

На рис. 24 соответственно изображены графики корреляционной линейной зависимости.

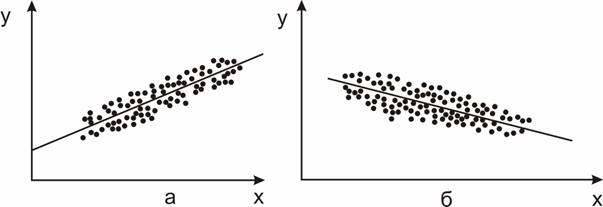
Рис. 24. Графики корреляционной линейной зависимости

Коэффициенты корреляции соответственно равны +0,9 (см. рис. 24а) и –0,9 (см. рис. 24б).

На рис. 24а с увеличением величины X величина y увеличивается, а на рис. 24б – наоборот уменьшается.

Корреляция может иметь и криволинейный характер (рис. 25).

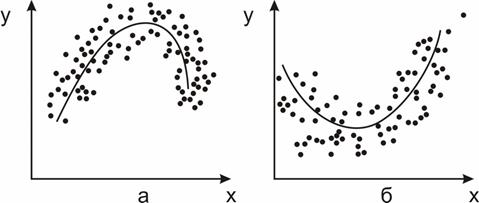
Рис. 25. Графики корреляционной зависимости (криволинейная корреляция)

Для выявления наличия или отсутствия причинно–следственных связей можно ограничиться только построением графика, (коэффициент корреляции можно не вычислять); но всегда необходимо дать логическое, профессиональное объяснение, чем данная зависимость, если она обнаружена, может быть обусловлена (вызвана).

С помощью корреляции можно грамотно решать многие вопросы. Например, установить зависимость точности обработки изделия от точностных параметров станка, технологического приспособления, различных параметров инструмента; определить зависимость микроструктуры металла от различных параметров электропечи (при термообработке); выяснять зависимость толщины покрытия от концентрации электролита и т.д. Спектр возможностей данного метода неограничен. Он находит широкое применение для решения различных технических, экономических, организационных, социальных и других проблем.