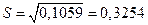| № п/п | Размер, мм | Отклонение от среднего
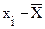
| Квадрат отклонения
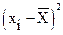
| Результирующие расчеты |
| 1 | 5,8 | –0,19 | 0,0361 | |
| 2 | 5,6 | –0,39 | 0,1521 | Сумма квадратов отклонений |
| 3 | 6,0 | 0,01 | 0,0001 |
|
| 4 | 5,7 | –0,29 | 0,0841 | |
| 5 | 5,6 | –0,39 | 0,1521 | |
| 6 | 6,3 | 0,31 | 0,0961 | |
| 7 | 6,4 | 0,41 | 0,1681 | Среднее арифметическое этой суммы |
| 8 | 6,0 | 0,01 | 0,0001 | |
| 9 | 6,1 | 0,11 | 0,0121 |
|
| 10 | 5,5 | –0,49 | 0,2401 | |
| 11 | 6,0 | 0,01 | 0,0001 | |
| 12 | 6,0 | 0,01 | 0,0001 | |
| 13 | 5,9 | –0,09 | 0,0081 | Среднее квадратическое отклонение |
| 14 | 6,0 | 0,01 | 0,0001 | |
| 15 | 5,8 | –0,19 | 0,0361 |
|
| 16 | 6,3 | 0,31 | 0,0961 | |
| 17 | 5,7 | –0,29 | 0,0841 | |
| 18 | 5,8 | –0,19 | 0,0361 | |
| 19 | 6,8 | 0,81 | 0,6561 | |
| 20 | 6,5 | 0,51 | 0,2601 |
Алгоритмы расчета среднего арифметического и среднего квадратического реализованы во всех отечественных и зарубежных микрокалькуляторах. При современном уровне развития вычислительной техники и современных требованиях к методам работы микрокалькуляторы должны найти широкое применение в практике промышленных предприятий, так как при этом резко уменьшается время, необходимое для выполнения расчетов, значительно повышаются надежность результатов и культура производства. Очень удобным и надежным является электронный микрокалькулятор БЗ–38. Он может быть использован для всех видов инженерных расчетов. Автоматически выполняет 34 операции, в том числе все необходимые статистические вычисления.
В табл. 9 рассчитано среднее квадратическое отклонение по результатам проверки выборки n из партии (генеральной совокупности).
Стандартное отклонение генеральной совокупности обозначается s и обычно оценивается по данным выборки.
В картах контроля по альтернативному признаку доля дефектных изделий Р и число дефектных изделий np распределяются по биномиальному закону. Исходя из физики явлений, обуславливающих характер распределения, выводится формула расчета стандартного отклонения для наблюдений, распределяющихся по биномиальному закону.
Если 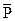 – средняя доля дефектных изделий, то
– средняя доля дефектных изделий, то
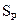 =
= 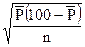 – формула расчета стандартного отклонения.
– формула расчета стандартного отклонения.
При контроле числа дефектных изделий
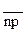 – среднее значение, то
– среднее значение, то
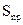 =
= 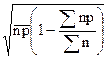 – формула расчета стандартного отклонения
– формула расчета стандартного отклонения
Суммарное число дефектов C и число дефектов на единицу продукции n распределяются по закону Пуассона. Исходя из свойств этого закона, если 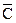 – среднее значение, то
– среднее значение, то 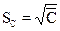
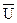 – среднее значение, то
– среднее значение, то 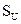 =
=  (см. карты контроля по альтернативному признаку)
(см. карты контроля по альтернативному признаку)
Карты контроля по количественному признаку представляют собой более трудоемкий метод по сравнению с картами P, np, С, U по трем причинам:
· требуется точное измерение наблюдаемых параметров (показателей) для всех проверяемых изделий;
· каждый параметр (показатель) требует одновременного применения двух карт (карты средних или медиан для наблюдения за тенденцией изменения среднего и карты размаха или стандартного отклонения для наблюдения за тенденцией изменения разброса, т.е. если нужно регулировать два показателя, например, диаметр валика и его длину, то в этом случае требуется четыре карты);
· большой объем вычислений.
Поэтому эти карты можно рекомендовать, главным образом, для проведения анализа технологического процесса (там, где с помощью карт P, np, С, U не удалось выяснить причины несоответствий), а также на стадии отладки технологии.
Расчет границ регулирования для карт 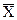 -R;
-R; 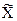 -R;
-R; 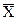 -S зависит от объема выборки, задач, которые должны быть решены с помощью контрольных карт, а также от того, имеет ли рассматриваемый показатель качества заданное стандартом или техническими условиями нормативное значение.
-S зависит от объема выборки, задач, которые должны быть решены с помощью контрольных карт, а также от того, имеет ли рассматриваемый показатель качества заданное стандартом или техническими условиями нормативное значение.
Рассмотрим порядок использования контрольных карт по количественному признаку для регулирования технологических процесса на примере карты 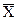 -R.
-R.
1. Отобрав мгновенную выборку объемом n (обычно 5–7 шт.) и измерив каждую деталь по исследуемому параметру, заносят результаты в контрольный листок (Бланк контрольного листка должен быть продуман и подготовлен заранее). Всего за период наблюдения за технологическим процессом отбирают 20–25 мгновенных выборок через определенные промежутки времени (К = 20 – 25).
2. Вычисляют среднее значение 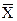 для каждой выборки
для каждой выборки 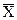 =
= 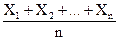
3. Рассчитывают размах R для каждой выборки R = 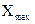 –
– 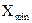
4. Предварительно подготовив бланки контрольных карт, на одной из них по вертикали наносят шкалу для 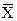 , а на другой – шкалу для R; по горизонтали – номер мгновенных выборок.
, а на другой – шкалу для R; по горизонтали – номер мгновенных выборок.
5. В бланки контрольных карт вносят точки значений 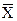 и R.
и R.
6. Вычисляют среднее 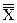 от
от 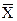 и среднее
и среднее 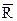 от R
от R
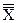 = = 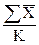
| (суммируются средние значения для всех выборок и полученная сумма делится на число выборок К). |
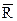 = = 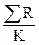
| (суммируются размахи для всех выборок и полученная сумма делится на число выборок K) |
7. Вычисляют границы регулирования 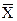 :
:
верхняя граница регулирования = 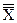 +
+ 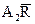 ;
;
нижняя граница регулирования = 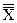 -
- 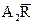 , где
, где
A2– коэффициент, зависящий от объема выборки n (табл. 10).
Таблица 10
Дата: 2019-02-24, просмотров: 362.
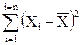 =2,1180.
=2,1180.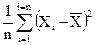 =
= 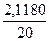 =0,1059
=0,1059