Если контрольные точки будут вписываться в пределы контрольных границ, то это свидетельствует о нормальном ходе процесса. В случае выхода за верхнюю контрольную границу необходимо установить причину повышенной дефектности с целью корректировки процесса сборки и обеспечения установленных норм.

Применение контрольного листка, представленного в табл.7 совместно с контрольной картой U дает очень хорошие результаты и позволяет существенно уменьшить дефектность, повысить стабильность и улучшить качество сложных технологических процессов, в том числе сборочных.

При использовании контрольных карт по альтернативному признаку (карты Р, np, С, U) проверяемая продукция подразделяется на годную и брак, при этом не фиксируются конкретные значения проверяемых параметров. Например, проверяем диаметр валика (размер по НТД 10±0,05 мм). На шкале измерительного прибора выставляется нижний и верхний предельные размеры 9,95 и 10,05. Если при проверке валика стрелка измерительного прибора находится внутри этих границ, то деталь годная, если за пределами какой–либо границы – деталь бракованная. Контрольные значения диаметра при этом не фиксируются, т.е. при контроле по альтернативному признаку средства измерения используются только с целью выявления случаев несоответствия проверяемой продукции установленным требованиям. Степень отклонения от установленных по НТД требований (т.е. конкретное численное значение проверяемого параметра) не фиксируется.

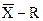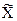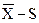Применение контрольных карт по количественному признаку (карты ; -R; ) требует оценки числового значения проверяемого параметра с установленной заранее точностью. Например, для случая с валиками 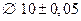мм: проверяется выборка n = 10. Применение какой–либо карты по количественному признаку требует знания конкретных значений диаметра всех проверяемых валиков (10,01; 10,03; 9,99; 10,04; и т.д.), т.е. при проверке n изделий по какому–то параметру следует иметь n конкретных значений. (В случае применения карты P необходима информация только о количестве дефектных изделий в выборке n – это одно число).

Рассмотрим основные понятия прикладной статистики, на которых основаны методы применения контрольных карт, в том числе карт по количественному признаку.

Генеральная совокупность

Генеральная совокупность представляет собой достаточно большое количество изделий, деталей. Это может быть количество изделий (деталей), изготовленных за час, смену, неделю или месяц, в зависимости от типа производства. Проверка всех изделий часто нецелесообразна из–за большой затраты времени и средств. Невозможно подвергать испытанию все изделия также и в том случае, когда – они при этом разрушаются. В обоих случаях следует ограничиться выборками из генеральной совокупности. С помощью статистических методов можно сделать вывод о свойствах, т.е. о числовых характеристиках (параметрах) гипотетической, большей частью бесконечно большой генеральной совокупности, использовав для этого одну или несколько выборок ограниченного объема (если проверяется партия продукции) или ряд выборок (если проверяется технологический процесс). В практике контроля под генеральной совокупностью понимается партия, поставка, подлежащая проверке, т.е. объем продукции N , качество которой требуется определить.

Выборка

Выборка представляет собой небольшое количество типичных образцов продукции n, взятых случайным образом из большой совокупности N.

При оценке состояния технологического процесса выборка n представляет собой ряд наблюдений, зафиксированных в определенной последовательности (через определенные промежутки времени) или непрерывные наблюдения. Методика комплектования выборки (сбора информации) в каждом конкретней случае определяется заранее, в зависимости от задач наблюдений, специфики производства, оговаривается в технологической документации. При использовании техники выборочных наблюдений и выполнении приемочного статистического контроля, важнейшим условием комплектования выборки является соблюдение принципа случайности. Каждое изделие должно иметь одинаковую вероятность попадания в выборку независимо от того, годное оно или дефектное. Методы отбора (комплектования) выборок, реализующие принцип случайности, рассмотрены в ГОСТ 18321–73.

При соблюдении принципа случайности комплектуется представительная выборка, т.е. выборка, которая хорошо представляет генеральную совокупность, отражает ее свойства (как бы является уменьшенным макетом генеральной совокупности).

При проведении статистического приемочного контроля объем выборки n, определяется по таблицам ГОСТ в зависимости от объема партии (поставки) N, уровня и вида контроля.

Контрольные карты можно применять на основе сплошного (когда проверяется 100% всей продукции) или выборочного контроля. При этом следует обратить особое внимание на то обстоятельство, что между контрольными картами, техникой приемочного выборочного контроля и техникой выборочных наблюдений существует принципиальная разница. При выборочном приемочном контроле и проведении техники выборочных наблюдений при образовании выборки ее элементы должны отбираться из проверяемой совокупности (партии) обязательно с соблюдением принципа случайности. При ведении контрольных карт на основе проверки выборок требование случайности отбора исключается. В этом случае в понятие выборки закладывается несколько иной смысл, и она называется мгновенной. Мгновенные выборки представляют собой выборки определенного объема, отбираемые через определенные интервалы времени по ходу технологического процесса. Единицы продукции мгновенной выборки должны отбираться с соблюдением принципа последовательности изготовления. Объем выборки n должен быть такой, чтобы она отражала только рассеивание процесса, а не его тренд. Период времени между мгновенными выборками должен назначаться таким, чтобы можно было проследить характер изменения процесса (тренд). На практике чаще всего используются мгновенные выборки n= 3, 5, 7, 9 (шт.)

Наблюдаемое значение

При использовании контрольных карт по альтернативному признаку наблюдаемые значения: P – доля дефектной продукции; np – число дефектных изделий; С – суммарное число дефектов; U – число дефектов на единицу продукции.

При проверке n изделий фиксируем одно число.

При использовании контрольных карт по количественному признаку наблюдаемым значением является конкретный проверяемый параметр, который измеряют с принятой по технологической документации точностью. Измеряемый параметр можно "закодировать" (обозначить) любой буквой латинского или русского алфавита, например а. Величина а часто определяется термином "показание", "наблюдение", "значение". Если у единицы продукции проверяется несколько показателей качества (параметров), то соответственно их можно обозначить а, b, c и т.д. Итак, если использовать какую–либо контрольную карту по количественному признаку для наблюдения за параметром а, то при проверке n изделий следует зафиксировать для каждого изделия значение параметра а, т.е. получить n значений:

a₁, a₂, a₃, … , a_n

Размах

Определяется как разность между максимальным и минимальным значениями проверяемого параметра. Обозначается буквой R. Например, проверим пять изделий по параметру a и получим следующие значения в мм: a₁=2,4; a₂=2,7; a₃=2,35; a₄=2,28; a₅=2,9;
R = a_max– a_min= a₅– a₄ = 2,9–2,28 = 0,62 мм. Размах R всегда больше нуля.

Среднее значение (среднее арифметическое)

Предположим, что проверяется n изделий. Измеряется параметр X и показания X₁, X₂, … , X_n (в мм) записываются в протокол или заносятся в память микрокалькулятора или ЭВМ.

Среднее арифметическое (среднее значение) обозначается соответствующей заглавной буквой с чертой 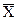 и получается сложением зафиксированных значений и делением полученной суммы на объем проверенных изделий n:

= =

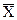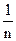
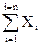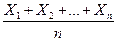
Например, выборка имеет пять изделий, которые измерены, а результаты измерений в миллиметрах записаны в протоколе: 2,4; 2,7; 2,7; 2,8; 2,9.

Тогда сумма 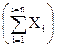 равна 13,5 мм.

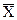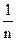
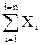= =13,5/5=2,7 мм.

Величина 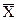 характеризует среднее положение наблюдаемых значений, около которого группируются (рассеивается) индивидуальные значения. Если построена гистограмма (см. рис. 6), то по гистограмме можно ориентировочно оценить  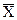– середина интервала с максимальной частотой.

Особенно легко определить медиану для небольшого количества измерений. Поэтому медиана часто встречается в технике контрольных карт, когда для наблюдения за технологическим процессом применяются небольшие выборки (n = 3, 5, 7, 9), отбираемые через определенные, заранее установленные промежутки времени. В остальных случаях целесообразнее использовать среднее арифметическое значение X, так как оно является более точной оценкой центра группирования.

Отклонение от среднего

Отклонение показания от среднего представляет собой разницу между величиной показания и средним значением. Так, если x – наблюдаемое значение, а 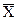 – среднее значение, то отклонение выражается величиной (x- 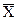). Рассмотрим пять показаний, приведенных выше. Отклонение показания x₁=2,4 от среднего 2,7 представляет собой
2,4 – 2,7 = – 0,3. Отклонение показания x₅=2,9 от среднего – соответственно 2,9 – 2,7 = 0,2. Отклонения от среднего могут быть положительными и отрицательными.

Среднее квадратическое (стандартное) отклонение

Для исчерпывающей оценки качества нужно знать среднее значение и разброс индивидуальных значения относительно среднего, т.е. необходимо иметь две характеристики, оценивающие проверяемую партию или производственный процесс. Одного среднего значения недостаточно, так как всегда имеет место рассеивание индивидуальных значение (показаний) относительно среднего арифметического. Чем теснее группируются индивидуальные значения относительно среднего, тем легче обеспечить стабильность качественных показателей. Наиболее точкой оценкой рассеивания является среднее квадратическое (стандартное) отклонение. Формулы для расчета S выводятся на основании закона распределения. Такие показатели качества, как длина, вес, твердость, толщина покрытия и т.д. (т.е. количественные показатели), как правило, распределяются по нормальному закону (закон Гаусса). Для применения карт контроля по количественному признаку S (стандартное отклонение) вычисляется путем возведения в квадрат величины каждого отклонения от среднего арифметического, суммирования всех квадратов и извлечения квадратного корня из среднего значения суммы.

S=	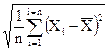– формула расчета стандартного отклонения для нормального распределения.

Среднее квадратическое (стандартное) отклонение имеет ту же размерность, что и среднее арифметическое.

В табл.9 приводится расчет среднего квадратического отклонения: n – объем выборки (n = 20); i – порядковый номер детали (i=1, 2, ..., 20); 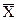– среднее арифметическое (X=5,99).

Таблица 9