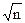
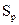
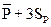
Число проверенных деталей n			Верхняя граница регулирования	Нижняя граница регулирования
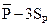
430	20,736	0,28	0,35+0,84=1,19	0,35–0,84<0
500	22,361	0,26	0,35+0,78=1,13	0,35–0,78<0
650	25,495	0,23	0,35+0,69=1,04	0,35–0,69<0
700	26,457	0,223	0,35+0,669=1,019	0,35–0,669<0
800	28,284	0,208	0,35+0,626=0,976	0,35–0,626<0

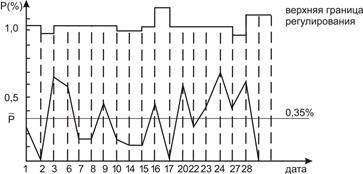
Рис. 11 Контрольная карта доли дефектных изделий P

Для случая с переменным объемом проверяемых выборок.

Представленные в табл.8 и на pис.11 результаты отражают свойства реального технологического процесса за февраль 1984 г. На основании приведенных данных можно сделать следующие выводы:

· в исследуемый (базисный) период процесс протекал достаточно точно и стабильно. Установлена средняя доля дефектных изделий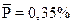

· на ближайший плановый период можно планировать такой уровень дефектности, т.е. ;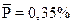

· учитывая результаты анализа технологического процесса, можно рекомендовать переход от сплошного контроля к выборочному, что приведет к сокращению трудозатрат на контроль;

· по результатам проверки выборок из партии следует осуществлять наблюдение за технологическим процессом c помощью контрольных карт P с целью своевременного обнаружения отклонений и их устранения.

Карта контроля числа дефектных изделий (np) строится аналогично. Она может применяться только тогда, когда объем проверяемых изделий n, является постоянным (n=const). В бланке контрольной карты по вертикали наносят деления для числа дефектных изделий np, обнаруженных при проверке изделий, а по горизонтали – дату или порядковый номер проверяемой выборки.

Вычисляют среднее 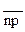 от np

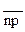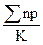= , где 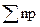– общее число дефектных изделий во всех выборках;

K - число проверенных выборок.

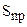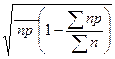=  – стандартное отклонение.

Верхняя граница регулирования = 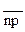+3 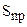; нижняя граница регулирования = 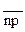-3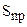

(Если при расчете нижней границы регулирования получается число, меньше нуля, то она принимается равной нулю). Выполним расчеты для примера, представленного в табл.5

(n=400=const)

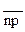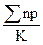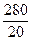= = =14,

.

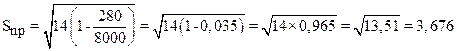Верхняя граница регулирования =14+3´3,676=14+11,028=25,028; нижняя граница регулирования =14–3´3,676=14–11,028=2,972.

На рис. 12 представлена контрольная карта числа дефектных изделий np, построенная по данным табл.5.

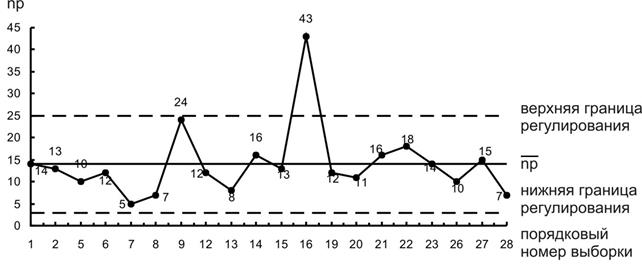
Рис.12. карта числа дефектных изделий ( np )

Рассмотренные контрольные карты (P и np) строятся на основе биномиального распределения. Оно описывает события, которые могут произойти, а могут и не произойти. Например, проверяемый образец может быть годным или дефектным. Однако в реальной действительности, включая и процессы контроля качества продукции, существует много ситуаций, при которых определение невыполнения (неосуществления) некоторого события вообще лишено смысла или является несущественным. Например, оценка числа дефектов в окраске панели прибора имеет смысл. Но оценка противоположного события, бессмысленна, как бессмысленна сама постановка вопроса о том, сколько таких дефектов отсутствует. Закон Пуассона может быть использован для изучения и контроля различных дефектов: окраски, изоляции провода, поверхности ткани, материала, сложных деталей, собранных механизмов.

С теоретической точки зрения необходимым условием применения закона Пуассона является неизменность среднего числа наступления рассматриваемых событий от испытания к испытанию. Как правило, перечисленные выше случаи отвечают изложенному требованию. В процессе анализа недопустимо смешение разнородных данных. Например, исследование и контроль дефектов при изготовлении эмалированной посуды различных размеров должны производиться для каждого размера отдельно. Аналогично, изучение дефектов гальванического покрытия должно выполняться для конкретной гальванической ванны дифференцированно для каждой продукции. В этом случае будет соблюдаться условие однородности статистических данных и неизменности среднего числа дефектов, приходящихся на одну деталь.