АНО «ЦЕНТР КВАЛИТЕТ»
Михайлова Н.В.

Учебное пособие
Москва 2009
Второе издание. Стереотипное.
Работа обсуждена и рекомендована к изданию на заседании кафедры "Метрология и контроль качества" МИПК Минприбора
Михайлова Н.В. Семь классических статистических методов обеспечения качества продукции и снижения издержек производства. Учебное пособие. – М., 1988. – 83 с, 12 табл., 26 рис., библ. 9 назв.
В пособии рассматриваются семь эффективных методов обеспечения качества: схема Исикавы, диаграмма Парето, гистограмма, контрольный листок, контрольные (управляющие) карты, расслоение, диаграмма зависимости (корреляция).
Пособие предназначено для руководителей и специалистов всех подразделений предприятия, включая рабочих. Рекомендуется для кураторов и членов групп качества.
Рецензенты: А.В. Гличев, д.э.н., проф. (ВНИИМИСП),
А.Н.Дубровский (МПЗ "Манометр").
ВВЕДЕНИЕ (Предисловие к первому изданию)
Постановление ЦК КПСС и Совета Министров СССР от 12 мая 1986 г. N 540 "О мерах по коренному повышению качества продукции" ориентирует на коренной перелом в методологии обеспечения качества.
Вопрос о качестве – это не лозунг, продиктованный временем, а насущная необходимость. Только повышая качество, можно говорить о конкурентоспособности, политическом престиже, ресурсосбережении, снижении себестоимости, росте фондоотдачи, совершенствовании структуры и организации производства, увеличении прибыли.
Задачи, стоящие перед отечественной промышленностью на современном этапе, требуют все более надежных и долговечных приборов, средств механизации к автоматизации, систем управления. Продукция, выпускаемая Минприбором, в большой степени определяет темп и уровень технического и научного прогресса в стране.
Повышение качества возможно только при условии привлечения к этой проблеме всех задействованных предприятий и организаций: разработчика, поставщика, изготовителя, потребителя. В сфере производства качеством ежедневно должны заниматься все подразделения предприятия, включая конкретных исполнителей.
Только такая техническая политика, когда за качество на каждом этапе, участке отвечает конкретный исполнитель, позволяет поставить на должный уровень методологию обеспечения качества и систему персональной ответственности.
В основе обеспечения качества лежит принцип профилактики дефектов (брака) на всех этапах жизненного цикла продукции: разработка – производство – потребление (эксплуатация). Задачи ОТК, а тем более Госприемки, не ограничиваются регистрацией, учетом, фиксированием качества выпускаемой продукции. Главное предназначение этих подразделений – анализ причин дефектов (недоработки конструкторской документации, дефекты элементной базы и комплектующих, отклонения в технологии, недоработки технологической документации, нарушение условий эксплуатации и т. д.) и последовательное, методичное их устранение. Реализация этого принципа требует постоянной, ежедневной, кропотливой работы по анализу продукции, технологии, комплектующих с точки зрения их соответствия требуемым стандартным нормам и принятия активных мер в случае отклонений от установленных норм. При этом самому серьезному контролю должны подвергаться все затраты на обеспечение качества продукции, т. е. контролю должны подвергаться: конструкторская разработка, готовая продукция, комплектующие, оборудование, технология, себестоимость, количество, сфера эксплуатации. При этом речь идет о таком контроле, который позволяет выявить причины дефектов. Классическая модель обеспечения качества продукции в процессе производства: постоянное наблюдение – своевременное выявление дефектов – установление причин дефектов – принятие мер по устранению причин дефектов. (Устранить нужно не сами дефекты, а их причины - в этом залог стабилизации качества выпускаемой продукции). Именно такой принцип реализуется на предприятиях Японии с 1949 г. В этом, главным образом, и состоит секрет "Японского чуда" – как принято сейчас говорить и писать. Тем не менее, следует четко уяснить, что это "Японское чудо" – результат многолетнего, кропотливого, почти ювелирного труда, по обеспечению качества, в котором участвуют все работающие на предприятии: от президента фирмы до рабочего. Причем труда – высокопрофессионального, с применением широкого спектра методов прикладной статистики. (Обучение этим методам всех работающих, включая рабочих, начато в 1949 г. и проводится по настоящее время по дифференцированным, из года в год расширяющимся программам) Статистические методы в Японии широко применяют во всех подразделениях фирмы на разных стадиях работ. "Нет такой области в деятельности фирмы, где не применялись бы статистические методы"[1], которые находят широкое применение не только в рамках фирмы. Применение этих методов является обязательным для поставщиков, субподрядных организаций, их широко используют в области посреднического бизнеса, в работе агентов по продаже, а также экономических подразделений. Диапазон применения различных статистических методов очень широк
[1 и 2].
Широкое применение статистических методов предусматривается группой стандартов ИСО 9000, ИСО 9001, ИСО 9002, ИСО 9003, ИСО 9004 [3]. В пособии излагаются семь наиболее простых и доступных методов, применение которых специалистами различных подразделений предприятия, включая рабочих, позволит развить статистическое мышление и серьезно улучшить комплекс работ по обеспечению качества в процессе производства. Эти методы дают прекрасный эффект при решении не только технических, но и экономических, организационных, социальных проблем. Сущность изложенных методов – конкретизация информации, представление ее в удобном для анализа виде. Причина их широкого распространения – универсальность. (Эти методы находят широкое применение не только на производстве, а и во всех областях научной и практической деятельности: медицине, фармакологии, сельском хозяйстве, географии и т.д.).
В СССР многие из приведенных ниже методов применялись в практике промышленных предприятий, а также при проведении различных исследований уже в
40–50–е годы. Тем не менее, в настоящее время в зарубежной и отечественной литературе пишут, а в научных кругах говорят о "семи японских методах" обеспечения качества. Из этих семи методов только один – схема Исикавы – действительно принадлежит крупному ученому Японии в области контроля качества – К. Исикава (почетный профессор Токийского университета, ректор промышленного института Мусаси). Все остальные методы интернациональны. Методы излагаются применительно к практике промышленного предприятия. Пособие предназначено для руководителей и специалистов всех подразделений предприятия, включая рабочих. Данные методы могут найти широкое применение и в практике научно–исследовательских институтов. Широкое применение изложенных методов в производственной практике позволит выявить узкие места, выработать правильную стратегию по их ликвидации, резко сократить издержки на брак. Максимальный эффект будет в том случае, если изложенными методами будут свободно владеть и применять на практике все работающие на предприятии, включая рабочих. (г. Москва 1988 г.)
I . СХЕМА ИСИКАВ Ы
Схема Исикавы[2] позволяет выявить и сгруппировать условия и факторы, влияющие на изучаемую проблему (рис. 1.).
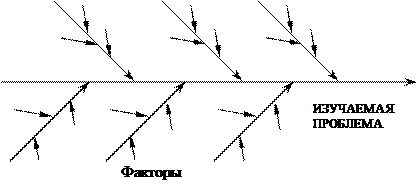
Рис 1. Общий вид причинно–следственной диаграммы
Изучаемая проблема условно изображается в виде прямой горизонтальной стрелки. Факторы, прямо или косвенно влияющие на проблему, изображаются наклонными стрелками. Должны выявляться и фиксироваться все факторы, даже те, которые кажутся незначительными, так как цель схемы Исикавы – отыскать наиболее правильный и эффективный способ решения поставленной проблемы. На практике достаточно часто встречаются случаи, когда можно добиться хороших результатов путем устранения нескольких, на первый взгляд несущественных причин.
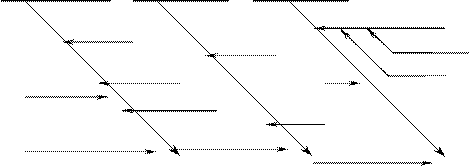
На рис.2 для примера приводится причинно–следственная диаграмма при анализе брака готового изделия.
 |
| ||||||||||
 | |||||||||||
 | |||||||||||
 |  |  | |||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис.2. Причинно–следственная диаграмма при анализе брака
Рекомендуется следующий порядок составления схемы Исикавы.
- Выбор проблемы для решения "узкого места" – прямая горизонтальная стрелка.
- Выявление наиболее существенных факторов, влияющих на проблему (причины первого порядка) – наклонные большие стрелки.
- Раскрытие существенных факторов – выявление причин, влияющих на эти факторы (причины второго, третьего и последующих порядков) – наклонные маленькие стрелки.
- Анализ и уточнение схемы: ранжирование факторов по их значимости; установление тех причин, которые в данный период времени поддаются корректировке.
- Установление уровня, до которого должны быть доведены факторы, подлежащие корректировке.
- Установление производственных участков, отделов, конкретных лиц, ответственных за доведение корректируемых факторов до установленного уровня.
- Разработка формы документа (или документов) с целью слежения за корректируемыми факторами. Установление конкретных лиц, ответственных за достоверность информации.
- Составление плана дальнейших действий – разработка мероприятий на перспективу. Установление ответственных лиц.
С помощью причинно–следственной диаграммы можно решать широкий спектр конструкторских, технологических, технических, организационных, экономических, социальных и других проблем.
ДИАГРАММА ПАРЕТО.
Диаграммы Парето (итальянский экономист 1845–1923) дают возможность объективно представить фактическое положение дел в понятной и наглядной форме.
На промышленных предприятиях актуальным вопросом является снижение потерь от брака. При анализе часто выявляется, что из десяти причин брака две–три являются основными и материальные потери от этих основных причин составляют 70–80% всех потерь. Для снижения потерь от брака важно вести работы в правильном направлении, а для этого необходимо выделить основные причины.
Простого коллективного обсуждения основных причин брака обычно недостаточно, так как мнения разных лиц и инстанций субъективны, не коррективны. В основе любого мероприятия должна лежать достоверная информация. Именно такую информацию позволяет получить диаграмма Парето (рис.3). При устранении причин 1 (нарушение технологической дисциплины), 2 (неудачная конструкция технологической оснастки), 4 (недостаточность освещения) количество брака можно снизить на 78%. Причем все указанные причины могут быть устранены силами самого предприятия, т.е. находятся в его компетенции.
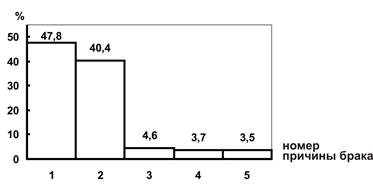
Рис.3. Диаграмма Парето по видам причин брака
Причины брака:
- нарушения технологической дисциплины на участке;
- неудачная конструкция технологической оснастки;
- дефекты в комплектующих изделиях;
- недостаточность освещения;
- прочие причины
На рис.4 представлена диаграмма Парето потерь по видам брака (в тыс. руб.)
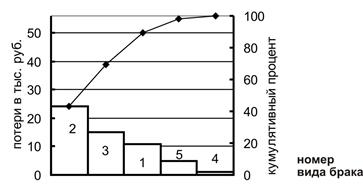
Рис.4. Диаграмма Парето потерь по видам брака
Причины потерь:
- брак по размерам (11 тыс. руб.);
- брак материалов (24 тыс. руб.);
- брак гальванического покрытия (15 тыс. руб.);
- брак заклепки (1 тыс. руб.);
- прочие виды брака (5 тыс. руб.).
На рис.3 весь брак принимается за 100%, а на рис.4 – все потери по видам брака принимаются за 100% (кумулятивный процент). (Кумулятивный – лат. cumulatio увеличение, скопление).
С помощью диаграмм Парето можно силами рядовых исполнителей, в том числе и рабочих, анализировать широкий круг проблем. Например:
Качество
- число случаев брака, по его видам;
- потери от брака по видам брака;
- затраты времени и материальных средств на исправление брака;
- содержание рекламаций, поступающих от потребителя;
- дефекты комплектующих;
- затраты, связанные с рекламациями;
- причины простоев;
- причины аварий, поломок технологического оборудования, оснастки, инструмента;
- причины несоблюдения технологической дисциплины и т.д.
Себестоимость
- суммы по отдельным статьям производственной схемы;
- затраты на обеспечение качества в процессе производства;
- затраты на производство (сырье, материалы, оплата труда, вспомогательные материалы, расходы на управление и т.д.);
- анализ отчетно-финансовой документации.
Безопасность труда
анализ причин несчастных случаев.
Спрос
анализ опроса на разные виды продукции.
Если рассмотрим диаграмму Парето (см. рис.4), то нетрудно определить, что очень большие потери (24 тыс. руб. – 42,85%) составляет брак материалов. В данном случае целесообразно поставить задачу снижения брака материалов, а для этого необходимо изучить отдельно виды брака материалов (табл.1).
Таблица 1
Виды брака материалов
| № п/п | Виды брака | Число случаев брака | Процентное соотношение, % | Кумулятивный процент, % |
| 1 | Надрезы и сколы | 32 | 66,7 | 66,7 |
| 2 | Трещины | 6 | 12,5 | 79,2 |
| 3 | Выщерблины | 5 | 10,4 | 89,6 |
| 4 | Прочие виды брака | 5 | 10,4 | 100,0 |
| Итого: | 48 | 100 |
На основе табл.1 строим диаграмму Парето (рис.5).
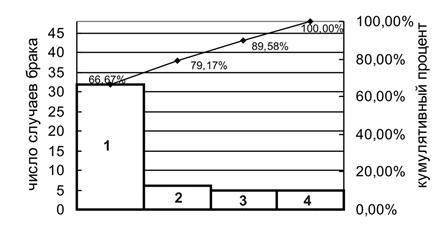
Рис.5. Диаграмма Парето по видам брака материалов
Причины брака:
- надрезы и сколы;
- трещины;
- выщерблины;
- прочие виды брака
Основные причины потерь по браку материалов (надрезы и сколы) составляют:
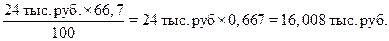
Аналогично можно подсчитать потери по другим видам брака материалов: из–за трещин – 3 тыс. руб., выщерблин – 2,496 тыс. руб., прочих видов брака – 2,496 тыс. руб.
Логика подсказывает, что целесообразно принять меры для уменьшения таких дефектов материала, как надрезы и сколы. Снизив эти дефекты на 50%, уменьшим потери по браку материалов на 8 тыс. руб.
Подобный анализ можно провести с целью выявления причин брака по размерам, а также причин брака гальванического покрытия (см. рис.4).
Данные, представленные на диаграмме Парето нужны для корректной оценки состояния и разработки мероприятий, направленных на устранение негативных факторов. Поэтому важно, чтобы этим вопросом владели непосредственные исполнителя – рабочие, контролеры, руководители производственных участков, начальники цехов, мастера, экономисты, технологи и т.д.
ГИСТОГРАММА
Основу любого анализа (исследования) составляют данные, полученные в результате контроля и измерения одного или нескольких параметров изделия (информация о качестве). Во всех без исключения отраслях промышленности требуется проведение анализа точности и стабильности технологических процессов, осуществление наблюдений за качеством продукции и улучшение различных производственных показателей.
Путем измерения параметров соответствующими средствами измерения получают ряд значений, называемый рядом измерений, который может состоять, например, из значений результатов измерений линейных размеров, погрешности формы, температуры плавки, твердости материала, количества телефонных вызовов в час на АТС, числа дефектов и т.д.
Ряд измерений представляет собой неупорядоченную последовательность значений параметра, поэтому на его основе невозможно сделать коррективные выводы. В табл.2 представлен протокол измерения диаметра колец: из партии N = 700 шт. отобрана выборка
n = 100, т.е. табл.2 – это ряд измерений.
Для аналитического осмысления информации о качестве (статистических данных) часто строят гистограмму распределения.
Таблица 2
Диаметр колец
| Протокол измерения колец, мм (n=100) | |||||||||
| 3,56 | 3,46 | 3,48 | 3,50 | 3,42 | 3,43 | 3,52 | 3,49 | 3,44 | 3,50 |
| 3,48 | 3,56 | 3,50 | 3,52 | 3,47 | 3,48 | 3,46 | 3,50 | 3,56 | 3,38 |
| 3,41 | 3,37 | 3,47 | 3,49 | 3,45 | 3,44 | 3,50 | 3,49 | 3,46 | 3,46 |
| 3,55 | 3,52 | 3,44 | 3,50 | 3,45 | 3,44 | 3,48 | 3,46 | 3,52 | 3,46 |
| 3,48 | 3,32 | 3,40 | 3,52 | 3,34 | 3,46 | 3,43 | 3,30 | 3,46 | 3,52 |
| 3,59 | 3,63 | 3,59 | 3,47 | 3,38 | 3,52 | 3,45 | 3,48 | 3,31 | 3,46 |
| 3,40 | 3,54 | 3,46 | 3,51 | 3,48 | 3,50 | 3,68 | 3,60 | 3,46 | 3,52 |
| 3,48 | 3,50 | 3,56 | 3,50 | 3,52 | 3,46 | 3,48 | 3,46 | 3,52 | 3,56 |
| 3,52 | 3,48 | 3,46 | 3,45 | 3,46 | 3,54 | 3,54 | 3,48 | 3,49 | 3,41 |
| 3,41 | 3,45 | 3,34 | 3,44 | 3,47 | 3,47 | 3,41 | 3,48 | 3,54 | 3,47 |
Гистограмма – это метод представления данных, сгруппированных по частоте попадания в определенный (заранее установленный) интервал. При простоте построения гистограмма дает много полезной аналитической информации о разбросе (рассеивании) качественных показателей, средних значениях, о точности и стабильности технологических процессов, о точностных возможностях технологического оборудования. Рассмотрим пример, представленный в табл.2.
Анализ этих данных позволяет установить наименьшее и наибольшее значение измеряемого параметра Xmin = 3,3 мм, Xmax = 3,68 мм. R = Xmin – Xmax = 0,38 мм. Разбиваем диапазон распределения интересующего нас параметра качества (в данном случае диаметра колец) на равные интервалы.
Надо учесть, что при слишком большом числе интервалов картина распределения будет искажена случайными зигзагами частот, слишком малочисленных при узких интервалах. При слишком малом числе интервалов характерные особенности распределения будут сглажены. Рекомендуется брать число интервалов (l) в пределах 8–10 при числе наблюдений 100–150. Для числа наблюдений 200–300 и более оптимальное число интервалов e = (10...20).
Для нашего примера выбираем e = 9. Тогда шаг разбиения (т.е. ширина каждого интервала) будет равен:
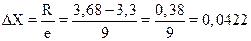 .
.
Для удобства построения назначим 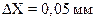 .
.
Подсчитаем теперь частоты по интервалам, расположив данные в виде табл.3.
Таблица 3
Распределение частот
| Порядковый номер интервала | Середина интервала | Границы интервала | Подсчет частот | Частота в интервале | Частость*) |
| 1 | 3,30 | 3,275 - 3,325 | III | 3 | 0,03 |
| 2 | 3,35 | 3,325 - 3,375 | III | 3 | 0,03 |
| 3 | 3,40 | 3,375 - 3,425 | | 9 | 0,09 |
| 4 | 3,45 | 3,425 - 3,475 | | 32 | 0,32 |
| 5 | 3,50 | 3,475 - 3,525 | | 38 | 0,38 |
| 6 | 3,55 | 3,525 - 3,575 | | 10 | 0,10 |
| 7 | 3,60 | 3,575 - 3,625 | III | 3 | 0,03 |
| 8 | 3,65 | 3,625 - 3,675 | I | 1 | 0,01 |
| 9 | 3,70 | 3,675 - 3,725 | I | 1
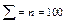
| 0,01
|
В столбец 4 заносят штриховые отметки, фиксирующие попадание измеренных значений (из табл.2) в интервал, указанный в столбце 3. Число штриховых отметок, т.е. частота попадания в каждый интервал, фиксируются в столбце 5.
Более наглядную картину дает графическое представление распределения частот с помощью гистограммы.
Гистограмма строится следующим образом: над каждым отрезком оси абсцисс, изображающим интервал значений, с центром в середине интервала, строится прямоугольник, высота которого пропорциональна частоте или частости в данном интервале (рис.6).
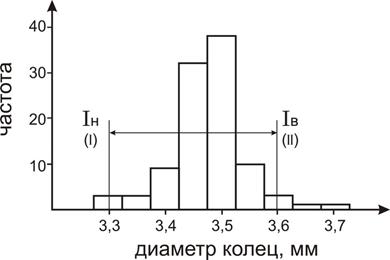
Рис.6. Гистограмма распределения:
I – нижний предел поля допуска;
II – верхний предел поля допуска
Благодаря наглядности и легкости построения гистограммы получили повсеместное применение как в области контроля качества, так и в области решения различных исследовательских проблем. В частности, метод гистограммы применяется при текущем контроле качества в процессе производства, при изучении возможностей технологических __________________________________________________
*) Частость – отношение частоты попадания в интервал к общему числу наблюдений
процессов. Гистограммы применяются для анализа работы отдельных исполнителей и станков, а также при обучении наладчиков, операторов и контролеров. Гистограммы находят широкое применение при составлении месячных отчетов цехов и заводов по качеству продукции, отчетов о результатах технического контроля, при иллюстрации изменений уровня качества по плановым периодам, а также при периодической плановой проверке точности оборудования.
КОНТРОЛЬНЫЙ ЛИСТОК
Контрольные листки используются при проведении текущего контроля заготовок, деталей, готовой продукции, сырья, полуфабрикатов и т.д.; при анализе оборудования и технологического процесса, при анализе брака и во многих других случаях. Форма листков разрабатывается в зависимости от поставленной задачи с целью сбора конкретных данных, необходимых и достаточных для решения поставленного вопроса. В предыдущем разделе показаны преимущества применения на производстве метода гистограмм. При рассмотрении практического примера прежде, чем построить гистограмму, необходимо систематизировать данные в виде таблицы (см. табл.3), которая является контрольным листком. Такие листки применяются часто при контроле готовых изделий. Рассмотрим пример: в механическом цехе обрабатывается деталь "ручка"  . Допуск – 0,08. Для проверки параметра применяется скоба 1271–2064. Результаты контроля приведены в табл.4 (контрольный листок).
. Допуск – 0,08. Для проверки параметра применяется скоба 1271–2064. Результаты контроля приведены в табл.4 (контрольный листок).
С помощью табл.4 устанавливается доля дефектности за каждый день и, кроме того, предусматривается расчет средней доли дефектности за месяц 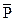 . В таблице фиксируется количество проверенных выборок K = 20. Такой контрольный листок позволяет осуществлять сбор данных за большой период времени и использовать эти данные в контрольных управляющих картах.
. В таблице фиксируется количество проверенных выборок K = 20. Такой контрольный листок позволяет осуществлять сбор данных за большой период времени и использовать эти данные в контрольных управляющих картах.
Таблица 4
Сведения о приемке детали "ручка"
| Дата (февраль 1984г.) | № п/п | Число проверенных деталей n, шт. | Число дефектных деталей X, шт. (np) | Доля дефектных деталей P, %
P= 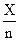 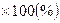
|
| 1 | 1 | 700 | 2 | 0,28 |
| 2 | 2 | 700 | 0 | 0 |
| 3 | 3 | 800 | 5 | 0,625 |
| 6 | 4 | 700 | 4 | 0,57 |
| 7 | 5 | 700 | 2 | 0,28 |
| 8 | 6 | 700 | 2 | 0,28 |
| 9 | 7 | 700 | 3 | 0,42 |
| 10 | 8 | 700 | 2 | 0,28 |
| 14 | 9 | 650 | 1 | 0,15 |
| 15 | 10 | 650 | 1 | 0,15 |
| 16 | 11 | 700 | 3 | 0,42 |
| 17 | 12 | 430 | 0 | 0 |
| 20 | 13 | 700 | 4 | 0,57 |
| 21 | 14 | 700 | 2 | 0,28 |
| 22 | 15 | 700 | 3 | 0,42 |
| 23 | 16 | 700 | 5 | 0,71 |
| 24 | 17 | 700 | 3 | 0,42 |
| 27 | 18 | 800 | 5 | 0,625 |
| 28 | 19 | 500 | 0 | 0 |
| 29 | 20 | 500 | 0 | 0 |
| Итого | К=20 | 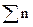 =13430 =13430
| 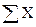 =47= =47= 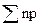
| 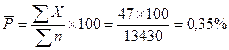
|
Аналогичный контрольный листок представлен в табл.5.
Таблица 5
| Дата (декабрь 1983г.) | Число проверенных манометров n, шт. | № п/п | Число дефектных манометров X, шт. (np) | Доля дефектных манометров P, %
P= 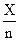 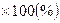
|
| 1 | 400 | 1 | 14 | 3,5 |
| 2 | 400 | 2 | 13 | 3,2 |
| 5 | 400 | 3 | 10 | 2,5 |
| 6 | 400 | 4 | 12 | 3,0 |
| 7 | 400 | 5 | 5 | 1,2 |
| 8 | 400 | 6 | 7 | 1,7 |
| 9 | 400 | 7 | 24 | 6,0 |
| 12 | 400 | 8 | 12 | 3,0 |
| 13 | 400 | 9 | 8 | 2,0 |
| 14 | 400 | 10 | 16 | 4,0 |
| 15 | 400 | 11 | 13 | 3,2 |
| 16 | 400 | 12 | 43 | 10,7 |
| 19 | 400 | 13 | 12 | 3,0 |
| 20 | 400 | 14 | 11 | 2,7 |
| 21 | 400 | 15 | 16 | 4,0 |
| 22 | 400 | 16 | 18 | 4,5 |
| 23 | 400 | 17 | 14 | 3,5 |
| 26 | 400 | 18 | 10 | 2,5 |
| 27 | 400 | 19 | 15 | 3,7 |
| 28 | 400 | 20 | 7 | 1,7 |
| Итого | 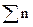 =8000 =8000
| К=20 | 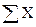 =280= =280= 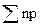
| 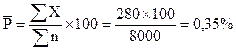
|
Контрольные листки, представленные в табл.4 и 5, фиксируют долю дефектности в %. Например, 2 декабря 1983 г. из 400 проверенных манометров – 13 дефектных, т.е. доля дефектности – 3,2%. Но при этом не фиксируется, какое число дефектов в неисправных манометрах. Дефектный прибор может иметь один, два или десять дефектов. На исправление одного дефекта потребуется намного меньше времени, чем на исправление десяти дефектов.
Когда проверяется сложная продукция часто целесообразно фиксировать число дефектов, приходящихся на единицу продукции.
Рассмотрим пример. В табл.6 приводятся результаты контроля печатных плат после металлизации. Проверено 10 партий (К = 10).
Таблица 6
Таблица 7
Дата
№ п. п.
В и д и к о д д е ф е к т а
Плохие разъёмы
Плохая изоляция провода
Неработоспособные ТЭЗы
Неправильно распаян кабель
Не работают светодиоды
Отказ источника питания
Рис.7. Бланк контрольного листка для учета дефектов окраски автомобиля
5. КОНТРОЛЬНЫЕ КАРТЫ [3]
Сущность контрольных карт
Контрольная карта графически отражает динамику процесса, т.е. изменение показателей качества во времени. На карте отмечен диапазон неизбежного рассеивания, который лежит в пределах верхней и нижней границ. Для оценки контрольных границ (границ регулирования) применяется трехкратное среднее квадратичное отклонение.
Контрольные карты находят широкое применение для анализа и регулирования технологических процессов.
Если точки, наносимые на контрольную карту, не выходят за границы регулирования, то технологический процесс считают протекающим стабильно. Такое расположение точек расценивают как неизбежное рассеивание показателей качества, и производство продолжают, ничего не изменяя.
Если же точки на карте выходят за контрольные границы, то считается, что в технологическом процессе возникли какие–то систематические погрешности, которые должны быть выявлены и устранены. Контрольные карты являются источником полезной информации, так как помимо рассеивания показателей качества позволяют дать вероятную оценку средних значений, т.е. уровня настройки технологического процесса. Благодаря указанным свойствам контрольные карты являются одним из эффективных средств анализа и совершенствования технологических процессов.
Классификация контрольных карт
Рассмотрим контрольные карты, применение которых наиболее целесообразно в производственной практике.
1. Контрольные карты по качественным (альтернативным) признакам: контрольная карта доли дефектных изделий (Р); контрольная карта числа дефектных изделий (np); контрольная карта суммарного числа дефектов (С); контрольная карта числа дефектов на единицу продукции (U).
2. Контрольные карты по количественным признакам: контрольная карта для средних значений и размаха 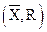 ; контрольная карта для медианы и размаха (
; контрольная карта для медианы и размаха ( 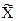 , R), контрольная карта для средних значений и среднего квадратического отклонения
, R), контрольная карта для средних значений и среднего квадратического отклонения 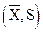 .
.
Границы регулирования
Границы регулирования – это линии, ограничивающие диапазон неизбежного рассеивания, т.е. рассеивания, вызванного неустранимыми (на данный период времени) причинами.
Границы регулирования на контрольных картах строятся от средней линии (center line) и называются верхней границей регулирования (upper control limit) и нижней границей регулирования (lower control limit) (рис.8).
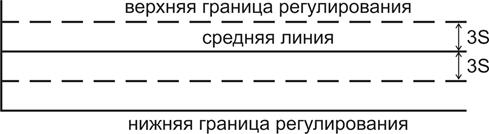
Рис.8. Границы регулирования
В ряде источников [2] верхняя и нижняя граница регулирования называются соответственно верхней и нижней контрольной границей.
Обычно диапазон от средней линии до границ регулирования содержит трехкратное среднее квадратическое (стандартное) отклонение.
Таким образом, границы регулирования определяют тот диапазон, внутри которого будут располагаться почти все точки, нанесенные на график, когда технологический процесс протекает стабильно, т.е. когда в нем отсутствуют непредвиденные (неожиданные) отклонения.
Карты контроля числа и доли дефектных изделий
Карты контроля числа и доли дефектных изделий получили наибольшее распространение в практике отечественных и зарубежных предприятий, так как они отличается гибкостью и наглядностью.
Рассмотрим пример. Имеем данные (см. табл.5) приемки контролером манометров за декабрь 1983 г. по цеху. Доля (процент) дефектных изделий (P), число бракованных изделий (np) статистически оцениваются биномиальным законом распределения. Теория биномиального распределения позволяет аналитически обобщить информацию о качестве продукции, которая представлена в табл.5.
Рассмотрим карту доли дефектных изделий (карта Р). Для этого рассчитываем необходимые статистические характеристики на основании биномиального распределения.
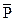 – среднее арифметическое значение
– среднее арифметическое значение
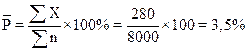 ,
,
где 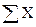 – суммарное число дефектных манометров,
– суммарное число дефектных манометров,
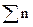 – суммарное число проверенных манометров.
– суммарное число проверенных манометров.
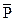 – средняя доля дефектных манометров,
– средняя доля дефектных манометров,
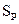 – среднее квадратическое (стандартное) отклонение.
– среднее квадратическое (стандартное) отклонение.
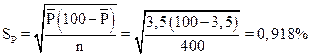
где n – объем выборки (в данном примере постоянный). На практике часто объем выборки меняется. Если объем выборки n меняется не очень существенно, то для расчета Sp можно применять простой и удобный метод, используя среднее 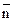 от n:
от n: 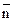 =
= 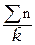 , где
, где 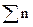 – суммарное число проверенных изделий за рассматриваемый период времени; k– суммарное число проверенных выборок (расчет SP по
– суммарное число проверенных изделий за рассматриваемый период времени; k– суммарное число проверенных выборок (расчет SP по 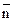 при переменном n не приведет к существенным погрешностям в том случае, если n для конкретных выборок изменяется относительно найденного по выше приведенной формуле
при переменном n не приведет к существенным погрешностям в том случае, если n для конкретных выборок изменяется относительно найденного по выше приведенной формуле 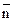 в пределах от 1/2 до 2 раз). Как правило, в реальном производстве имеют место изменения объемов выборок в указанных пределах.
в пределах от 1/2 до 2 раз). Как правило, в реальном производстве имеют место изменения объемов выборок в указанных пределах.
Посмотрим контрольную карту P (рис.9) для нашего примера.
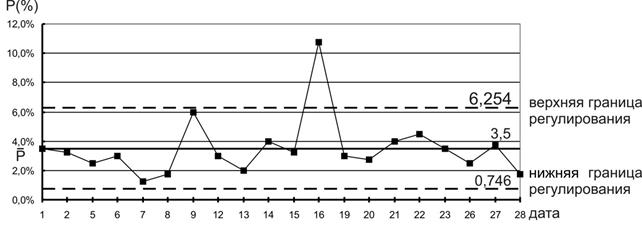
Рис.9. Контрольная карта доли дефектных изделий P (%).
В бланке контрольной карты по вертикали откладываем долю дефектных изделий в процентах Р (%), а по горизонтали – дату или номера выборок.
Значение 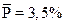 определяет положение средней линии. Верхняя граница регулирования определяется:
определяет положение средней линии. Верхняя граница регулирования определяется:
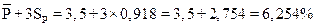
а нижняя граница регулирования определяется:
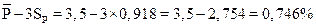
Результаты представленные в табл.5 и на рис.9, отражают контроль реального процесса за декабрь 1983 г. Данные о контроле необходимы для следующих целей:
· констатации реального уровня дефектности в наблюдаемый (исследуемый, базисный) период;
· анализа процесса и определения реальных возможностей на ближайший плановый период.
Анализируя данные, видим, что 16 декабря доля дефектных манометров (P = 10,7%) выходит за пределы верхней контрольной границы. Удалось установить причину высокой дефектности 16 декабря – использование регулировщицей с индексом 24 контрольного манометра, неправильно размеченного работниками метрологической лаборатории. Причина была устранена. 9 декабря доля дефектных манометров тоже достаточно высока (приближается к верхней границе), но причину дефектности выявить не удалось. Поэтому при расчете реального уровня дефектности на ближайший плановый период (январь 1984 г.) можно исключить только значения за 16 декабря, так как если не планировать проведение определенных оргтехмероприятий, то есть все основания предположить, что в январе 1984 г. будут иметь место все те причинно–следственные связи при производстве манометров, какие были в исследуемом (базисном) периоде (декабрь 1983 г.) за исключением причины, выявленной 16 декабря (последняя была устранена).
Рассчитываем реальный уровень дефектности на январь 1984 г. (ближайший период) и строим бланк для контрольной карты (рис. 10).

Рис.10 Бланк контрольной карты доли дефектных изделий P (%) на январь 1984г.
При расчете данных для контрольной карты на январь 1984 г. исключаем значения, полученные 16 декабря 1983 г. (400 манометров, из которых 43 – дефектных). Поэтому:
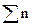 =8000-400=7600
=8000-400=7600
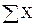 =280-43=237
=280-43=237
Расчет выполняется по выше приведенным формулам:
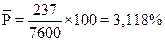
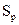 =
= 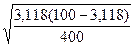 =0,869%
=0,869%
верхняя граница регулирования = 3,118 + 3×0,869= 5,725%,
нижняя граница регулирования = 3,118 – 3×0,869= 0,511%.
Из расчетов видно, что в январе можно ожидать некоторое улучшение качественных показателей. Результаты контроля, вписывающиеся в пределы контрольных границ, свидетельствуют о нормальном ходе процесса. Каждый выход за верхнюю контрольную границу должен фиксироваться и сразу тщательно разбираться с целью выявления и устранения причин дефектов. Проведение такой планомерной работы будет способствовать не только стабилизации, но и улучшению качества, так как постепенно будут выявляться наиболее существенные и часто повторяющиеся причины дефектов.
Техника контрольной карты позволяет также устанавливать дни с низким уровнем дефектности, а следовательно выявлять сложившиеся производственные ситуации, способствующие наилучшим качественным показателям.
Работа с контрольной картой помогает реализовать на практике принцип диагностики процесса, своевременной его корректировки и грамотного, обоснованного планирования оргтехмероприятий, направленных на существенное улучшение качественных показателей.
В рассмотренном выше примере число проверяемых изделий постоянно. В практике предприятий часто объем проверяемых изделий заметно меняется. В этом случае также эффективно применение контрольных карт.
Рассмотрим пример, представленный в табл.4, в котором с 1 февраля по 29 февраля было проверено 20 выборок разного объема.
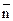 =
= 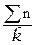 =
= 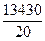 =671,5
=671,5
Наименьшее количество проверяемых деталей – 430 (порядковый номер – 12), 430/671,5 = 0,640; наибольшее количество – 800, 800/671,5=1,193, т.е. изменения конкретных объемов проверяемых по отношению к среднему значению лежат в пределах от 1/2 до 2. Поэтому все расчеты можно выполнять по приведенным выше формулам, пренебрегая тем, что n – переменно.
Однако для тех, кто хочет выполнить расчеты более тщательно, продемонстрируем на данном примере, как видоизменяется процедура расчета границ регулирования и построения контрольной карты с учетом переменного n. Рассчитываем среднюю долю дефектных изделий:
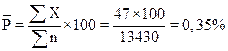
При колебании объемов проверяемых изделий стандартное отклонение рассчитываем по формуле:
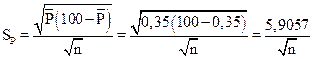 ,
,
где n — переменная величина.
Верхняя граница регулирования 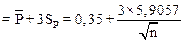 ;
;
нижняя граница регулирования 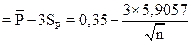 .
.
(Если нижняя граница регулирования по расчетам меньше нуля, то она принимается равной нулю).
В табл.8 представлен расчет верхней и нижней границ регулирования, а на рис.11 построена контрольная карта P для рассматриваемого примера.
Таблица 8
Рис. 11 Контрольная карта доли дефектных изделий P
Рис.12. карта числа дефектных изделий ( np )
Рассмотренные контрольные карты (P и np) строятся на основе биномиального распределения. Оно описывает события, которые могут произойти, а могут и не произойти. Например, проверяемый образец может быть годным или дефектным. Однако в реальной действительности, включая и процессы контроля качества продукции, существует много ситуаций, при которых определение невыполнения (неосуществления) некоторого события вообще лишено смысла или является несущественным. Например, оценка числа дефектов в окраске панели прибора имеет смысл. Но оценка противоположного события, бессмысленна, как бессмысленна сама постановка вопроса о том, сколько таких дефектов отсутствует. Закон Пуассона может быть использован для изучения и контроля различных дефектов: окраски, изоляции провода, поверхности ткани, материала, сложных деталей, собранных механизмов.
С теоретической точки зрения необходимым условием применения закона Пуассона является неизменность среднего числа наступления рассматриваемых событий от испытания к испытанию. Как правило, перечисленные выше случаи отвечают изложенному требованию. В процессе анализа недопустимо смешение разнородных данных. Например, исследование и контроль дефектов при изготовлении эмалированной посуды различных размеров должны производиться для каждого размера отдельно. Аналогично, изучение дефектов гальванического покрытия должно выполняться для конкретной гальванической ванны дифференцированно для каждой продукции. В этом случае будет соблюдаться условие однородности статистических данных и неизменности среднего числа дефектов, приходящихся на одну деталь.
Рис. 13 контрольная карта суммарного числа дефектов C
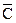 – среднее значение
– среднее значение 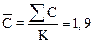 ;
;
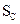 – стандартное отклонение
– стандартное отклонение 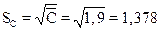 ;
;
верхняя граница регулирования 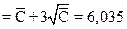 ;
;
нижняя граница регулирования 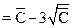 принимается равной нулю.
принимается равной нулю.
(Если при расчете нижней границы регулирования получается число меньше нуля, то нижняя граница регулирования принимается равной нулю).
На бланке карты C по вертикали откладывают суммарное число дефектов, а по горизонтали дату или номера выборок (постоянного объема).
Как видно из рис. 13 контрольные точки на карте C вписываются в пределы верхней и нижней границ регулирования, что свидетельствует о нормальном ходе технологического процесса. Если зафиксированное состояние технологического процесса по качественным показателям устраивает предприятие, то полученные значения ( 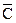 , верхняя и нижняя границы регулирования) можно принять, как стандартные нормы на ближайший плановый период и выполнять контроль за техпроцессом на основе этих данных. При этом, если в результате очередной проверки окажется, что контрольная точка резко приближается или выходит за верхнюю границу регулирования, то необходимо срочно разобраться в ситуации с целью устранения установленных негативных факторов.
, верхняя и нижняя границы регулирования) можно принять, как стандартные нормы на ближайший плановый период и выполнять контроль за техпроцессом на основе этих данных. При этом, если в результате очередной проверки окажется, что контрольная точка резко приближается или выходит за верхнюю границу регулирования, то необходимо срочно разобраться в ситуации с целью устранения установленных негативных факторов.
Карта контроля числа дефектов на единицу продукции
Карта контроля числа дефектов на единицу продукции (карта U) является более удобной (по сравнению с картой С), так как может применяться и при условии переменного числа проверяемых изделий (n), а также более информативной: число дефектов на единицу продукции – конкретный показатель технологического процесса, особенно когда речь идет об исправлении дефектов. (Суммарное число дефектов является несколько "размытой" оценкой).
Построим карту U для рассмотренного выше примера (см. табл.6):
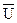 – среднее значение
– среднее значение 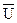 =
= 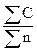 =
= 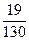 =0,146;
=0,146;
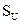 – стандартное отклонение
– стандартное отклонение 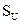 =
= 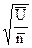 =
= 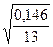 =0,106;
=0,106;
верхняя граница регулирования 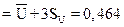 ;
;
нижняя граница регулирования 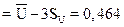 принимается равной нулю.
принимается равной нулю.
Если n переменно, то SU можно рассчитывать по среднему значению 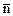 . Тогда
. Тогда 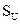 =
= 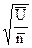 . (Если отношение конкретных значений проверяемых изделий n к
. (Если отношение конкретных значений проверяемых изделий n к 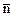 лежит в пределах от 1/2 до 2, то можно при расчете SU применять
лежит в пределах от 1/2 до 2, то можно при расчете SU применять 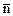 ). На рис.14 приведена карта U. По вертикали откладывается число дефектов на единицу продукции, а по горизонтали – дата или порядковый номер проверяемой выборки.
). На рис.14 приведена карта U. По вертикали откладывается число дефектов на единицу продукции, а по горизонтали – дата или порядковый номер проверяемой выборки.
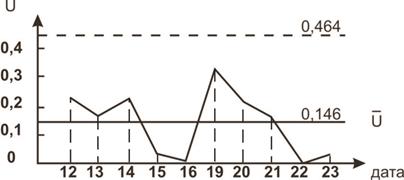
Рис.14. Контрольная карта U (числа дефектов на единицу продукции).
Построим контрольную карту U для случая, представленного в табл.7 – контроль сложного сборочного процесса, когда важно иметь корректную информацию не только по числу дефектов на единицу продукции, но также информацию о частоте появления различных дефектов. Контрольный листок (табл.7) является очень удобной формой слежения за сложным сборочным процессом (или сложным процессом механообработки и т.д.). Но его можно дополнить картой U. Для нашего случая: 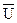 =
= 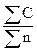 =
= 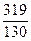 =2,45. Количество проверяемых изделий за один рабочий день n изменялось незначительно (от четырех до шести). Поэтому расчет
=2,45. Количество проверяемых изделий за один рабочий день n изменялось незначительно (от четырех до шести). Поэтому расчет 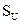 можно выполнять по
можно выполнять по 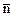 .
.
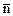 =
= 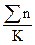 =
= 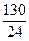 =5,41, где K – число рабочих дней.
=5,41, где K – число рабочих дней.
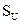 =
= 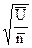 =
= 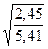 =0,6729
=0,6729
верхняя граница регулирования = 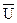 +3
+3 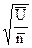 =4,468,
=4,468,
нижняя граница регулирования = 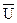 -3
-3 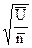 =0,432.
=0,432.
Полученные значения 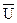 , верхней и нижней границ регулирования характеризуют процесс сборки за исследуемый (базисный) период – декабрь. После проведения анализа процесса, выявления наиболее часто встречающихся дефектов, установления причин некоторых дефектов и принятия мер по их устранению, можно ожидать, что в январе процесс сборки изделия A будет иметь меньшую дефектность. После проведенных мероприятий есть все основания предположить, что дефекты 1а и 3 не должны иметь место. Следовательно, при расчете реально достижимых норм на ближайший плановый период (январь) дефекты 1а и 3 можно исключить. Тогда получим:
, верхней и нижней границ регулирования характеризуют процесс сборки за исследуемый (базисный) период – декабрь. После проведения анализа процесса, выявления наиболее часто встречающихся дефектов, установления причин некоторых дефектов и принятия мер по их устранению, можно ожидать, что в январе процесс сборки изделия A будет иметь меньшую дефектность. После проведенных мероприятий есть все основания предположить, что дефекты 1а и 3 не должны иметь место. Следовательно, при расчете реально достижимых норм на ближайший плановый период (январь) дефекты 1а и 3 можно исключить. Тогда получим:
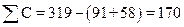
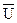 =
= 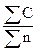 =
= 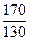 =1,307 (130 –месячная программа)
=1,307 (130 –месячная программа)
верхняя граница регулирования = 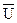 +3
+3 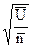 =2,777,
=2,777,
нижняя граница регулирования = 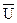 -3
-3 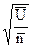 <0.
<0.
нижняя граница регулирования принимается равной нулю.
Построим бланк контрольной карты U для наблюдения за сборочным процессом изделия А в январе (рис.15).
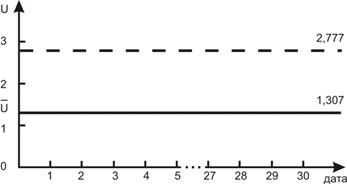
Рис.15 бланк контрольной карты на январь для наблюдения
Генеральная совокупность
Генеральная совокупность представляет собой достаточно большое количество изделий, деталей. Это может быть количество изделий (деталей), изготовленных за час, смену, неделю или месяц, в зависимости от типа производства. Проверка всех изделий часто нецелесообразна из–за большой затраты времени и средств. Невозможно подвергать испытанию все изделия также и в том случае, когда – они при этом разрушаются. В обоих случаях следует ограничиться выборками из генеральной совокупности. С помощью статистических методов можно сделать вывод о свойствах, т.е. о числовых характеристиках (параметрах) гипотетической, большей частью бесконечно большой генеральной совокупности, использовав для этого одну или несколько выборок ограниченного объема (если проверяется партия продукции) или ряд выборок (если проверяется технологический процесс). В практике контроля под генеральной совокупностью понимается партия, поставка, подлежащая проверке, т.е. объем продукции N , качество которой требуется определить.
Выборка
Выборка представляет собой небольшое количество типичных образцов продукции n, взятых случайным образом из большой совокупности N.
При оценке состояния технологического процесса выборка n представляет собой ряд наблюдений, зафиксированных в определенной последовательности (через определенные промежутки времени) или непрерывные наблюдения. Методика комплектования выборки (сбора информации) в каждом конкретней случае определяется заранее, в зависимости от задач наблюдений, специфики производства, оговаривается в технологической документации. При использовании техники выборочных наблюдений и выполнении приемочного статистического контроля, важнейшим условием комплектования выборки является соблюдение принципа случайности. Каждое изделие должно иметь одинаковую вероятность попадания в выборку независимо от того, годное оно или дефектное. Методы отбора (комплектования) выборок, реализующие принцип случайности, рассмотрены в ГОСТ 18321–73.
При соблюдении принципа случайности комплектуется представительная выборка, т.е. выборка, которая хорошо представляет генеральную совокупность, отражает ее свойства (как бы является уменьшенным макетом генеральной совокупности).
При проведении статистического приемочного контроля объем выборки n, определяется по таблицам ГОСТ в зависимости от объема партии (поставки) N, уровня и вида контроля.
Контрольные карты можно применять на основе сплошного (когда проверяется 100% всей продукции) или выборочного контроля. При этом следует обратить особое внимание на то обстоятельство, что между контрольными картами, техникой приемочного выборочного контроля и техникой выборочных наблюдений существует принципиальная разница. При выборочном приемочном контроле и проведении техники выборочных наблюдений при образовании выборки ее элементы должны отбираться из проверяемой совокупности (партии) обязательно с соблюдением принципа случайности. При ведении контрольных карт на основе проверки выборок требование случайности отбора исключается. В этом случае в понятие выборки закладывается несколько иной смысл, и она называется мгновенной. Мгновенные выборки представляют собой выборки определенного объема, отбираемые через определенные интервалы времени по ходу технологического процесса. Единицы продукции мгновенной выборки должны отбираться с соблюдением принципа последовательности изготовления. Объем выборки n должен быть такой, чтобы она отражала только рассеивание процесса, а не его тренд. Период времени между мгновенными выборками должен назначаться таким, чтобы можно было проследить характер изменения процесса (тренд). На практике чаще всего используются мгновенные выборки n= 3, 5, 7, 9 (шт.)
Наблюдаемое значение
При использовании контрольных карт по альтернативному признаку наблюдаемые значения: P – доля дефектной продукции; np – число дефектных изделий; С – суммарное число дефектов; U – число дефектов на единицу продукции.
При проверке n изделий фиксируем одно число.
При использовании контрольных карт по количественному признаку наблюдаемым значением является конкретный проверяемый параметр, который измеряют с принятой по технологической документации точностью. Измеряемый параметр можно "закодировать" (обозначить) любой буквой латинского или русского алфавита, например а. Величина а часто определяется термином "показание", "наблюдение", "значение". Если у единицы продукции проверяется несколько показателей качества (параметров), то соответственно их можно обозначить а, b, c и т.д. Итак, если использовать какую–либо контрольную карту по количественному признаку для наблюдения за параметром а, то при проверке n изделий следует зафиксировать для каждого изделия значение параметра а, т.е. получить n значений:
a1, a2, a3, … , an
Размах
Определяется как разность между максимальным и минимальным значениями проверяемого параметра. Обозначается буквой R. Например, проверим пять изделий по параметру a и получим следующие значения в мм: a1=2,4; a2=2,7; a3=2,35; a4=2,28; a5=2,9;
R = amax– amin= a5– a4 = 2,9–2,28 = 0,62 мм. Размах R всегда больше нуля.
Среднее значение (среднее арифметическое)
Предположим, что проверяется n изделий. Измеряется параметр X и показания X1, X2, … , Xn (в мм) записываются в протокол или заносятся в память микрокалькулятора или ЭВМ.
Среднее арифметическое (среднее значение) обозначается соответствующей заглавной буквой с чертой 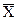 и получается сложением зафиксированных значений и делением полученной суммы на объем проверенных изделий n:
и получается сложением зафиксированных значений и делением полученной суммы на объем проверенных изделий n:
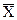 =
= 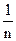
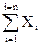 =
= 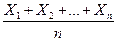
Например, выборка имеет пять изделий, которые измерены, а результаты измерений в миллиметрах записаны в протоколе: 2,4; 2,7; 2,7; 2,8; 2,9.
Тогда сумма 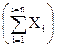 равна 13,5 мм.
равна 13,5 мм.
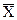 =
= 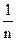
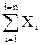 =13,5/5=2,7 мм.
=13,5/5=2,7 мм.
Величина 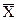 характеризует среднее положение наблюдаемых значений, около которого группируются (рассеивается) индивидуальные значения. Если построена гистограмма (см. рис. 6), то по гистограмме можно ориентировочно оценить
характеризует среднее положение наблюдаемых значений, около которого группируются (рассеивается) индивидуальные значения. Если построена гистограмма (см. рис. 6), то по гистограмме можно ориентировочно оценить 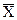 – середина интервала с максимальной частотой.
– середина интервала с максимальной частотой.
Особенно легко определить медиану для небольшого количества измерений. Поэтому медиана часто встречается в технике контрольных карт, когда для наблюдения за технологическим процессом применяются небольшие выборки (n = 3, 5, 7, 9), отбираемые через определенные, заранее установленные промежутки времени. В остальных случаях целесообразнее использовать среднее арифметическое значение X, так как оно является более точной оценкой центра группирования.
Отклонение от среднего
Отклонение показания от среднего представляет собой разницу между величиной показания и средним значением. Так, если x – наблюдаемое значение, а 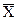 – среднее значение, то отклонение выражается величиной (x-
– среднее значение, то отклонение выражается величиной (x- 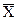 ). Рассмотрим пять показаний, приведенных выше. Отклонение показания x1=2,4 от среднего 2,7 представляет собой
). Рассмотрим пять показаний, приведенных выше. Отклонение показания x1=2,4 от среднего 2,7 представляет собой
2,4 – 2,7 = – 0,3. Отклонение показания x5=2,9 от среднего – соответственно 2,9 – 2,7 = 0,2. Отклонения от среднего могут быть положительными и отрицательными.
Среднее квадратическое (стандартное) отклонение
Для исчерпывающей оценки качества нужно знать среднее значение и разброс индивидуальных значения относительно среднего, т.е. необходимо иметь две характеристики, оценивающие проверяемую партию или производственный процесс. Одного среднего значения недостаточно, так как всегда имеет место рассеивание индивидуальных значение (показаний) относительно среднего арифметического. Чем теснее группируются индивидуальные значения относительно среднего, тем легче обеспечить стабильность качественных показателей. Наиболее точкой оценкой рассеивания является среднее квадратическое (стандартное) отклонение. Формулы для расчета S выводятся на основании закона распределения. Такие показатели качества, как длина, вес, твердость, толщина покрытия и т.д. (т.е. количественные показатели), как правило, распределяются по нормальному закону (закон Гаусса). Для применения карт контроля по количественному признаку S (стандартное отклонение) вычисляется путем возведения в квадрат величины каждого отклонения от среднего арифметического, суммирования всех квадратов и извлечения квадратного корня из среднего значения суммы.
S= 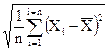
| – формула расчета стандартного отклонения для нормального распределения. |
Среднее квадратическое (стандартное) отклонение имеет ту же размерность, что и среднее арифметическое.
В табл.9 приводится расчет среднего квадратического отклонения: n – объем выборки (n = 20); i – порядковый номер детали (i=1, 2, ..., 20); 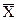 – среднее арифметическое (X=5,99).
– среднее арифметическое (X=5,99).
Таблица 9
Таблица 10
РАССЛОЕНИЕ
Сущность статистической концепции заключается в том, что решения принимаются только на основе достоверных и корректных данных. Расслоение, как статистический метод, применяется для получения корректной информации. Рассмотрим сначала несколько примеров, не имеющих отношения к технике.
Например, является ли корректным такой показатель, как потребление овощей на душу населения в СССР? Наверное, учитывая большую разницу в климатических условиях, целесообразнее оценить этот показатель отдельно для районов Кавказа, Средней Азии, Дальнего востока, Мурманской области и т. д. В этом случае получим объективную оценку и столкнемся с тем фактом, что потребление овощей на душу населения на Кавказе, например, несоизмеримо выше, чем в Мурманской области. Проведя такой анализ, мы выполнили расслоение по климатическим (территориальным) признакам.
Другой пример – из области медицины, например, требуется определить процент больных сахарным диабетом в каком–то отдельном регионе. Очевидно, что такой показатель для статистики может представлять какой–то определенный смысл. Но если определять этот показатель для различных возрастных категорий, то оценки будут более информативны с точки зрения профилактики заболевания. Например, процент больных диабетом в возрасте
1–5 лет, 6–10 лет, 11–15 лет, 16–20 лет в т. д.
Теперь рассмотрим пример из производственной практики: в цехе 10 токарно-револьверных станков, на которых изготавливается одноименная продукция. Обнаружено, что брак по данному участку составляет 4%. Можно ли на основании этой цифры разработать какие–либо конкретные мероприятия, направленные на уменьшение брака? Очевидно, что нельзя. Наверное, надо определить процент брака с каждого конкретного станка, т. е. выполнить расслоение по станкам. Когда будет известен процент брака для каждого станка отдельно, тогда можно оценить, какой станок требует профилактики. Допустим, известно, что со станка № 3 выходит продукция с засоренностью дефектными 12%. Для того, чтобы снизить эту дефектность нужно найти ее причину, а для этого необходимо провести анализ причин дефектности, т. е. выяснить какие факторы вызывают дефектность и установить те факторы, которые оказывают наибольшее влияние на нее. Для разработки конкретных мероприятий, направленных на уменьшение дефектности станка № 3 нужно выполнить расслоение по причинам дефектности.
При рассмотрении диаграммы Парето уже выполнялась процедура расслоения. На рис. 4 представлена диаграмма Парето потерь по видам брака, из которой видно, что брак материалов – 24 тыс. руб. (42, 85% общей суммы потерь). Затем был выполнен анализ брака материалов, на основании которого составлена табл. 1 и построена диаграмма Парето по видам брака материалов (см. рис. 5). Следовательно, расслоение применяется для выявления действия отдельных причин на какую–либо величину или явление. Применение метода расслоения позволяет получать достоверные данные. В Японии считают, что "без расслоения нет прогресса контроля качества" [6]. Как метод исследования, позволяющий выявить причинно–следственные связи, расслоение применяется очень давно. В основе метода расслоения лежит понятие расслоенной выборки. "Расслоенная выборка – выборка, разбитая на несколько выборок меньших объемов по некоторым отличительным признакам" [7].
Рассмотрим конкретный пример, наглядно иллюстрирующий эффективность применения метода расслоения в производственной практике: станочник обслуживает три шестишпиндельных токарных станка. ОТК при приемочном контроле бракует по параметру B последовательно несколько партий продукции, изготовленной на этих трех станках. При проведении разбраковки возвращенных станочнику партий установлено, что в этих партиях засоренность дефектными варьировала от 4% до 6%. По технологической документации допускается дефектность 1,5% (если засоренность дефектными деталями меньше или равна 1,5%, партия принимается, если больше 1,5% – бракуется). В данном случае 1,5% – приемлемый уровень качества. В зависимости от AQL по ГОСТ назначаются планы контроля (См. ГОСТ Р 50779.71-99; взамен ГОСТ 18242–72 ).
Для того, чтобы разобраться в причинах брака был проверен следующий анализ:
1. Отбирались выборки для каждого станка, т. е. выполнено расслоение по станкам. По результатам проверки выборок построены гистограммы (рис. 16), из анализа которых ясно, что причиной повышенной дефектности является станок № 1.
2. Учитывая, что шестишпиндельный токарный станок практически ведет себя как шестистаночный агрегат, в котором работают одновременно все станки, выполнялось расслоение по шпинделям (для станка № 1), т. е. отбирались выборки для каждого шпинделя отдельно. По результатам проверенных выборок построены (рис. 17) для каждого шпинделя контрольные карты (карты 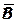 – карты средних арифметических для параметра B).
– карты средних арифметических для параметра B).
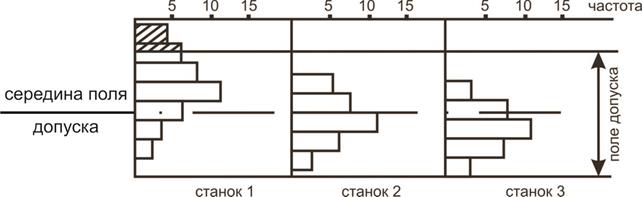
Рис.16 Гистограмма (распределение) по станкам.
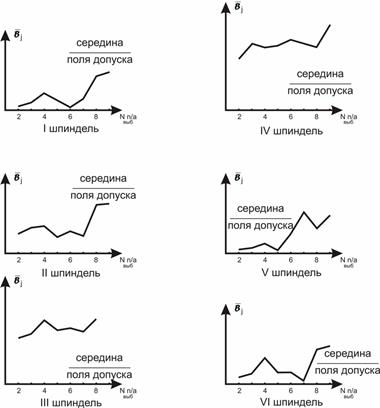
Рис. 17. Контрольные карты средних арифметических для параметра B (расслоение по шпинделям) j – порядковый номер выборки.
Эти карты позволяют проследить изменение настройки во времени. Из приведенных карт 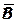 видно, что относительно правильно выполнена настройка только шпинделя V. Все остальные шпиндели нуждаются в регулировке.
видно, что относительно правильно выполнена настройка только шпинделя V. Все остальные шпиндели нуждаются в регулировке.
По результатам проверки мгновенных выборок для каждого шпинделя построены кривые, характеризующие разброс (рассеивание) параметра B (Рис. 18).
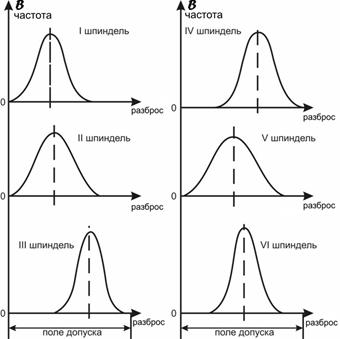
Рис.18. Разброс по параметру B . (Расслоение по шпинделям)
Для шпинделей I, Ш, IV, VI реальный разброс несколько меньше поля допуска, а для шпинделей II и V реальный разброс равен полю допуска. Следовательно, причина брака заключается в плохой настройке шпинделей на середину поля допуска.
В целях устранения причин брака наладчиком проведена работа по отладке шпинделей. Затем для каждого шпинделя были проведены контрольные испытания, по результатам которых построены контрольные карты средних арифметических. На рис. 19 приведена контрольная карта 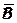 для шпинделя I (для остальных шпинделей карты
для шпинделя I (для остальных шпинделей карты 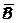 аналогичны). Из приведенной контрольной карты видно, что настройка шпинделя выполнена правильно, так как контрольные точки средних значений разбросаны почти симметрично относительно середины поля допуска.
аналогичны). Из приведенной контрольной карты видно, что настройка шпинделя выполнена правильно, так как контрольные точки средних значений разбросаны почти симметрично относительно середины поля допуска.
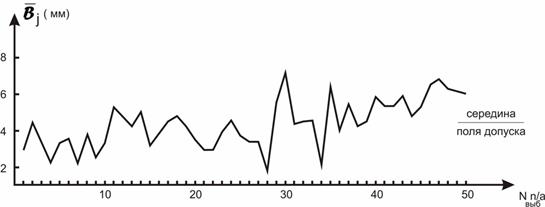
Рис. 19. Контрольная карта средних арифметических для параметра 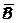 (шпиндель I )
(шпиндель I )
После проведенных мероприятий принято решение выполнять периодическую проверку всех трех станков по выше изложенному принципу, так как производство массовое, разбраковка партий и издержки на брак обходятся очень дорого.
В течение длительного времени возвратов продукции, изготовляемой на этих трех станках, не зафиксировано. Это объясняется тем, что периодическая проверка станков (с расслоениями по шпинделям) направлена на профилактику брака.
Рис. 20. График корреляционной зависимости между параметрам A и B .
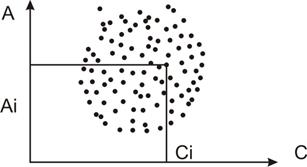
Рис. 21. График корреляционной зависимости между параметрами A и C .
Таблица 11
Контрольный листок
| № п/п | Проверяемые параметры | |||
| A | B | C | Д | |
| 1 | A1 | B1 | C1 | Д1 |
| 2 | A2 | B2 | C2 | Д2 |
| 3 | A3 | B3 | C3 | Д3 |
| … | ||||
| Ai | Bi | Ci | Дi | |
| … | ||||
| An–1 | Bn–1 | Cn–1 | Дn–1 | |
| An | Bn | Cn | Дn | |
| Итого n | 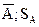
| 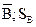
| 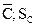
| 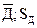
|
По контрольному листку можно построить графики зависимости между: А–В; А–С; А–Д; В–С; В–Д; С–Д. Например, если по оси абсцисс отложить значение параметра В для первой детали (B1), а по оси ординат – значение параметра А для этой же детали (A1), то на графике получим одну точку с координатами B1, A1. Проделав аналогичную процедуру для всех n значений, получим на графике n точек (см. рис. 20). Следовательно, можно сделать вывод о наличия зависимости между параметрами A и B. Численно степень зависимости можно оценить величиной коэффициента корреляции r по формуле:
r= 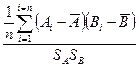 ,
,
где Ai и Bi значения параметров A и B для i-й детали;
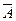 ,
, 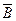 – средние арифметические значения величин A и B;
– средние арифметические значения величин A и B;
SA, SB – стандартные отклонения величин А и В;
n – число изделий в выборке (объем выборки).
Рекомендуемое значение n, для выполнения корреляционного анализа: n 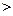 30.
30.
Коэффициент корреляции определяется по формуле:
r= 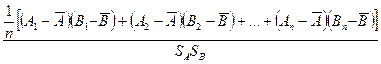
Точки, нанесенные на график в прямоугольной системе координат, образуют так называемое "поле корреляции". Если зависимость имеет место, то поле корреляции вытянуто и направление "вытянутости" не совпадает с направлением осей координат. Если величины независимы, то поле корреляции параллельно одной из осей координат или имеет форму круга (см. рис. 21). Графический анализ позволяет установить наличие зависимости и приблизительно оценить степень этой зависимости. Например, можно утверждать, что зависимость между параметрами A и Д (рис. 22) сильнее, чем между параметрами A и B (см. рис. 21) т.е. более тесная связь. Для количественной оценки такой связи между двумя величинами нужно знать коэффициент корреляции r. Причем, если r= 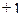 , то это свидетельствует о наличии функциональной зависимости. Если r=0, то величины независимы. Чем ближе значение коэффициента корреляции к 1, тем теснее зависимость между параметрами.
, то это свидетельствует о наличии функциональной зависимости. Если r=0, то величины независимы. Чем ближе значение коэффициента корреляции к 1, тем теснее зависимость между параметрами.
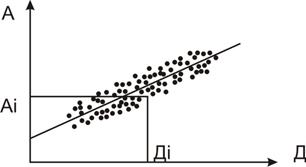
Рис. 22. График корреляционной зависимости между параметрами A и Д.
На рис. 23а изображена прямая линейная зависимость (r=+1), на рис. 23б – обратная линейная зависимость (r=-1).
Рис. 23. Графики линейной зависимости
На рис. 24 соответственно изображены графики корреляционной линейной зависимости.
Рис. 24. Графики корреляционной линейной зависимости
Коэффициенты корреляции соответственно равны +0,9 (см. рис. 24а) и –0,9 (см. рис. 24б).
На рис. 24а с увеличением величины X величина y увеличивается, а на рис. 24б – наоборот уменьшается.
Корреляция может иметь и криволинейный характер (рис. 25).
Рис. 25. Графики корреляционной зависимости (криволинейная корреляция)
Для выявления наличия или отсутствия причинно–следственных связей можно ограничиться только построением графика, (коэффициент корреляции можно не вычислять); но всегда необходимо дать логическое, профессиональное объяснение, чем данная зависимость, если она обнаружена, может быть обусловлена (вызвана).
С помощью корреляции можно грамотно решать многие вопросы. Например, установить зависимость точности обработки изделия от точностных параметров станка, технологического приспособления, различных параметров инструмента; определить зависимость микроструктуры металла от различных параметров электропечи (при термообработке); выяснять зависимость толщины покрытия от концентрации электролита и т.д. Спектр возможностей данного метода неограничен. Он находит широкое применение для решения различных технических, экономических, организационных, социальных и других проблем.
Рис. 26. Ход реализации работ по устранению дефектов.
Таблица 12
ЛИТЕРАТУРА
1. Курицын А. Н. Управление в Японии. – М.: Наука, 1981.
2. Саката Сиро. Практическое руководство по управлению качеством. /пер. в 4–го Яп. изд. – М.: Машиностроение, 1980.
3. Стандарты МС ИСО серии 9000.
4. Методы обеспечения качества продукции в Японии. – М.: Изд. во стандартов, 1970.
5. Э. Шиндовский, О. Шюрц. Статистические методы управления качеством. Контрольные карты и планы контроля. /Пер. с нем. – М.: Мир, 1976.
6. Каору Исикава. Контроль качества продукции в Японии. Японские методы управления качеством. – М.: Экономика, 1988.
7. Математическая энциклопедия. Т. 4. –М.: Сов. энциклопедия, 1984.
8. Айвазян С. А. Статистическое исследование зависимостей. (Применение методов корреляционного и регрессионного анализов к обработке результатов эксперимента), – М,: Металлургия, 1968.
9. Методы снижения издержек производства. Пер. с англ., нем., яп. –М., Экономика, 1987.
ОГЛАВЛЕНИЕ
ВВЕДЕНИЕ.. 3
I. Схема Исикавы.. 4
2. Диаграмма Парето. 6
3. Гистограмма. 8
4.Контролькый листок. 11
5. Контрольные карты.. 17
6. Расслоение. 35
7. Диаграмма разброса (корреляция) 38
8. Снижение издержек производства. Статистический подход. 42
ЛИТЕРАТУРА.. 45
Михайлова Нина Викторовна, к. т. н.
Семь статистических методов обеспечения качества
продукции и снижения издержек производства
Учебное пособие
[1] Some features of quality control in Japan. In: International conference of quality control, 1969. То kyo, 1969. p. l6–18
[2] В литературе часто встречается под следующими названиями: диаграмма "причина–следствие", "рыбья кость", "рыбий скелет".
[3] Карты, требующие корректирующих мер
АНО «ЦЕНТР КВАЛИТЕТ»
Михайлова Н.В.

Учебное пособие
Москва 2009
Второе издание. Стереотипное.
Работа обсуждена и рекомендована к изданию на заседании кафедры "Метрология и контроль качества" МИПК Минприбора
Михайлова Н.В. Семь классических статистических методов обеспечения качества продукции и снижения издержек производства. Учебное пособие. – М., 1988. – 83 с, 12 табл., 26 рис., библ. 9 назв.
В пособии рассматриваются семь эффективных методов обеспечения качества: схема Исикавы, диаграмма Парето, гистограмма, контрольный листок, контрольные (управляющие) карты, расслоение, диаграмма зависимости (корреляция).
Пособие предназначено для руководителей и специалистов всех подразделений предприятия, включая рабочих. Рекомендуется для кураторов и членов групп качества.
Рецензенты: А.В. Гличев, д.э.н., проф. (ВНИИМИСП),
А.Н.Дубровский (МПЗ "Манометр").
ВВЕДЕНИЕ (Предисловие к первому изданию)
Постановление ЦК КПСС и Совета Министров СССР от 12 мая 1986 г. N 540 "О мерах по коренному повышению качества продукции" ориентирует на коренной перелом в методологии обеспечения качества.
Вопрос о качестве – это не лозунг, продиктованный временем, а насущная необходимость. Только повышая качество, можно говорить о конкурентоспособности, политическом престиже, ресурсосбережении, снижении себестоимости, росте фондоотдачи, совершенствовании структуры и организации производства, увеличении прибыли.
Задачи, стоящие перед отечественной промышленностью на современном этапе, требуют все более надежных и долговечных приборов, средств механизации к автоматизации, систем управления. Продукция, выпускаемая Минприбором, в большой степени определяет темп и уровень технического и научного прогресса в стране.
Повышение качества возможно только при условии привлечения к этой проблеме всех задействованных предприятий и организаций: разработчика, поставщика, изготовителя, потребителя. В сфере производства качеством ежедневно должны заниматься все подразделения предприятия, включая конкретных исполнителей.
Только такая техническая политика, когда за качество на каждом этапе, участке отвечает конкретный исполнитель, позволяет поставить на должный уровень методологию обеспечения качества и систему персональной ответственности.
В основе обеспечения качества лежит принцип профилактики дефектов (брака) на всех этапах жизненного цикла продукции: разработка – производство – потребление (эксплуатация). Задачи ОТК, а тем более Госприемки, не ограничиваются регистрацией, учетом, фиксированием качества выпускаемой продукции. Главное предназначение этих подразделений – анализ причин дефектов (недоработки конструкторской документации, дефекты элементной базы и комплектующих, отклонения в технологии, недоработки технологической документации, нарушение условий эксплуатации и т. д.) и последовательное, методичное их устранение. Реализация этого принципа требует постоянной, ежедневной, кропотливой работы по анализу продукции, технологии, комплектующих с точки зрения их соответствия требуемым стандартным нормам и принятия активных мер в случае отклонений от установленных норм. При этом самому серьезному контролю должны подвергаться все затраты на обеспечение качества продукции, т. е. контролю должны подвергаться: конструкторская разработка, готовая продукция, комплектующие, оборудование, технология, себестоимость, количество, сфера эксплуатации. При этом речь идет о таком контроле, который позволяет выявить причины дефектов. Классическая модель обеспечения качества продукции в процессе производства: постоянное наблюдение – своевременное выявление дефектов – установление причин дефектов – принятие мер по устранению причин дефектов. (Устранить нужно не сами дефекты, а их причины - в этом залог стабилизации качества выпускаемой продукции). Именно такой принцип реализуется на предприятиях Японии с 1949 г. В этом, главным образом, и состоит секрет "Японского чуда" – как принято сейчас говорить и писать. Тем не менее, следует четко уяснить, что это "Японское чудо" – результат многолетнего, кропотливого, почти ювелирного труда, по обеспечению качества, в котором участвуют все работающие на предприятии: от президента фирмы до рабочего. Причем труда – высокопрофессионального, с применением широкого спектра методов прикладной статистики. (Обучение этим методам всех работающих, включая рабочих, начато в 1949 г. и проводится по настоящее время по дифференцированным, из года в год расширяющимся программам) Статистические методы в Японии широко применяют во всех подразделениях фирмы на разных стадиях работ. "Нет такой области в деятельности фирмы, где не применялись бы статистические методы"[1], которые находят широкое применение не только в рамках фирмы. Применение этих методов является обязательным для поставщиков, субподрядных организаций, их широко используют в области посреднического бизнеса, в работе агентов по продаже, а также экономических подразделений. Диапазон применения различных статистических методов очень широк
[1 и 2].
Широкое применение статистических методов предусматривается группой стандартов ИСО 9000, ИСО 9001, ИСО 9002, ИСО 9003, ИСО 9004 [3]. В пособии излагаются семь наиболее простых и доступных методов, применение которых специалистами различных подразделений предприятия, включая рабочих, позволит развить статистическое мышление и серьезно улучшить комплекс работ по обеспечению качества в процессе производства. Эти методы дают прекрасный эффект при решении не только технических, но и экономических, организационных, социальных проблем. Сущность изложенных методов – конкретизация информации, представление ее в удобном для анализа виде. Причина их широкого распространения – универсальность. (Эти методы находят широкое применение не только на производстве, а и во всех областях научной и практической деятельности: медицине, фармакологии, сельском хозяйстве, географии и т.д.).
В СССР многие из приведенных ниже методов применялись в практике промышленных предприятий, а также при проведении различных исследований уже в
40–50–е годы. Тем не менее, в настоящее время в зарубежной и отечественной литературе пишут, а в научных кругах говорят о "семи японских методах" обеспечения качества. Из этих семи методов только один – схема Исикавы – действительно принадлежит крупному ученому Японии в области контроля качества – К. Исикава (почетный профессор Токийского университета, ректор промышленного института Мусаси). Все остальные методы интернациональны. Методы излагаются применительно к практике промышленного предприятия. Пособие предназначено для руководителей и специалистов всех подразделений предприятия, включая рабочих. Данные методы могут найти широкое применение и в практике научно–исследовательских институтов. Широкое применение изложенных методов в производственной практике позволит выявить узкие места, выработать правильную стратегию по их ликвидации, резко сократить издержки на брак. Максимальный эффект будет в том случае, если изложенными методами будут свободно владеть и применять на практике все работающие на предприятии, включая рабочих. (г. Москва 1988 г.)
I . СХЕМА ИСИКАВ Ы
Схема Исикавы[2] позволяет выявить и сгруппировать условия и факторы, влияющие на изучаемую проблему (рис. 1.).
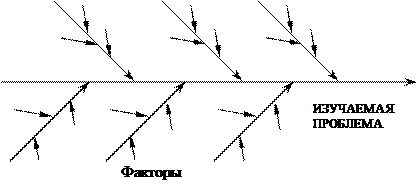
Рис 1. Общий вид причинно–следственной диаграммы
Изучаемая проблема условно изображается в виде прямой горизонтальной стрелки. Факторы, прямо или косвенно влияющие на проблему, изображаются наклонными стрелками. Должны выявляться и фиксироваться все факторы, даже те, которые кажутся незначительными, так как цель схемы Исикавы – отыскать наиболее правильный и эффективный способ решения поставленной проблемы. На практике достаточно часто встречаются случаи, когда можно добиться хороших результатов путем устранения нескольких, на первый взгляд несущественных причин.
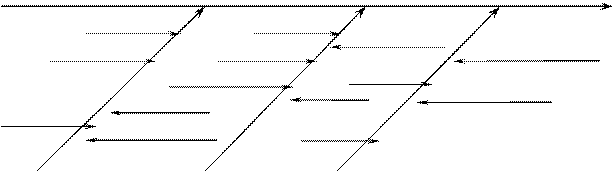
На рис.2 для примера приводится причинно–следственная диаграмма при анализе брака готового изделия.
 |
| ||||||||||
 | |||||||||||
 | |||||||||||
 |  |  | |||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис.2. Причинно–следственная диаграмма при анализе брака
Рекомендуется следующий порядок составления схемы Исикавы.
- Выбор проблемы для решения "узкого места" – прямая горизонтальная стрелка.
- Выявление наиболее существенных факторов, влияющих на проблему (причины первого порядка) – наклонные большие стрелки.
- Раскрытие существенных факторов – выявление причин, влияющих на эти факторы (причины второго, третьего и последующих порядков) – наклонные маленькие стрелки.
- Анализ и уточнение схемы: ранжирование факторов по их значимости; установление тех причин, которые в данный период времени поддаются корректировке.
- Установление уровня, до которого должны быть доведены факторы, подлежащие корректировке.
- Установление производственных участков, отделов, конкретных лиц, ответственных за доведение корректируемых факторов до установленного уровня.
- Разработка формы документа (или документов) с целью слежения за корректируемыми факторами. Установление конкретных лиц, ответственных за достоверность информации.
- Составление плана дальнейших действий – разработка мероприятий на перспективу. Установление ответственных лиц.
С помощью причинно–следственной диаграммы можно решать широкий спектр конструкторских, технологических, технических, организационных, экономических, социальных и других проблем.
ДИАГРАММА ПАРЕТО.
Диаграммы Парето (итальянский экономист 1845–1923) дают возможность объективно представить фактическое положение дел в понятной и наглядной форме.
На промышленных предприятиях актуальным вопросом является снижение потерь от брака. При анализе часто выявляется, что из десяти причин брака две–три являются основными и материальные потери от этих основных причин составляют 70–80% всех потерь. Для снижения потерь от брака важно вести работы в правильном направлении, а для этого необходимо выделить основные причины.
Простого коллективного обсуждения основных причин брака обычно недостаточно, так как мнения разных лиц и инстанций субъективны, не коррективны. В основе любого мероприятия должна лежать достоверная информация. Именно такую информацию позволяет получить диаграмма Парето (рис.3). При устранении причин 1 (нарушение технологической дисциплины), 2 (неудачная конструкция технологической оснастки), 4 (недостаточность освещения) количество брака можно снизить на 78%. Причем все указанные причины могут быть устранены силами самого предприятия, т.е. находятся в его компетенции.

Рис.3. Диаграмма Парето по видам причин брака
Причины брака:
- нарушения технологической дисциплины на участке;
- неудачная конструкция технологической оснастки;
- дефекты в комплектующих изделиях;
- недостаточность освещения;
- прочие причины
На рис.4 представлена диаграмма Парето потерь по видам брака (в тыс. руб.)

Рис.4. Диаграмма Парето потерь по видам брака
Причины потерь:
- брак по размерам (11 тыс. руб.);
- брак материалов (24 тыс. руб.);
- брак гальванического покрытия (15 тыс. руб.);
- брак заклепки (1 тыс. руб.);
- прочие виды брака (5 тыс. руб.).
На рис.3 весь брак принимается за 100%, а на рис.4 – все потери по видам брака принимаются за 100% (кумулятивный процент). (Кумулятивный – лат. cumulatio увеличение, скопление).
С помощью диаграмм Парето можно силами рядовых исполнителей, в том числе и рабочих, анализировать широкий круг проблем. Например:
Качество
- число случаев брака, по его видам;
- потери от брака по видам брака;
- затраты времени и материальных средств на исправление брака;
- содержание рекламаций, поступающих от потребителя;
- дефекты комплектующих;
- затраты, связанные с рекламациями;
- причины простоев;
- причины аварий, поломок технологического оборудования, оснастки, инструмента;
- причины несоблюдения технологической дисциплины и т.д.
Себестоимость
- суммы по отдельным статьям производственной схемы;
- затраты на обеспечение качества в процессе производства;
- затраты на производство (сырье, материалы, оплата труда, вспомогательные материалы, расходы на управление и т.д.);
- анализ отчетно-финансовой документации.
Безопасность труда
анализ причин несчастных случаев.
Спрос
анализ опроса на разные виды продукции.
Если рассмотрим диаграмму Парето (см. рис.4), то нетрудно определить, что очень большие потери (24 тыс. руб. – 42,85%) составляет брак материалов. В данном случае целесообразно поставить задачу снижения брака материалов, а для этого необходимо изучить отдельно виды брака материалов (табл.1).
Таблица 1
Виды брака материалов
| № п/п | Виды брака | Число случаев брака | Процентное соотношение, % | Кумулятивный процент, % |
| 1 | Надрезы и сколы | 32 | 66,7 | 66,7 |
| 2 | Трещины | 6 | 12,5 | 79,2 |
| 3 | Выщерблины | 5 | 10,4 | 89,6 |
| 4 | Прочие виды брака | 5 | 10,4 | 100,0 |
| Итого: | 48 | 100 |
На основе табл.1 строим диаграмму Парето (рис.5).

Рис.5. Диаграмма Парето по видам брака материалов
Причины брака:
- надрезы и сколы;
- трещины;
- выщерблины;
- прочие виды брака
Основные причины потерь по браку материалов (надрезы и сколы) составляют:
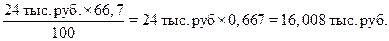
Аналогично можно подсчитать потери по другим видам брака материалов: из–за трещин – 3 тыс. руб., выщерблин – 2,496 тыс. руб., прочих видов брака – 2,496 тыс. руб.
Логика подсказывает, что целесообразно принять меры для уменьшения таких дефектов материала, как надрезы и сколы. Снизив эти дефекты на 50%, уменьшим потери по браку материалов на 8 тыс. руб.
Подобный анализ можно провести с целью выявления причин брака по размерам, а также причин брака гальванического покрытия (см. рис.4).
Данные, представленные на диаграмме Парето нужны для корректной оценки состояния и разработки мероприятий, направленных на устранение негативных факторов. Поэтому важно, чтобы этим вопросом владели непосредственные исполнителя – рабочие, контролеры, руководители производственных участков, начальники цехов, мастера, экономисты, технологи и т.д.
ГИСТОГРАММА
Основу любого анализа (исследования) составляют данные, полученные в результате контроля и измерения одного или нескольких параметров изделия (информация о качестве). Во всех без исключения отраслях промышленности требуется проведение анализа точности и стабильности технологических процессов, осуществление наблюдений за качеством продукции и улучшение различных производственных показателей.
Путем измерения параметров соответствующими средствами измерения получают ряд значений, называемый рядом измерений, который может состоять, например, из значений результатов измерений линейных размеров, погрешности формы, температуры плавки, твердости материала, количества телефонных вызовов в час на АТС, числа дефектов и т.д.
Ряд измерений представляет собой неупорядоченную последовательность значений параметра, поэтому на его основе невозможно сделать коррективные выводы. В табл.2 представлен протокол измерения диаметра колец: из партии N = 700 шт. отобрана выборка
n = 100, т.е. табл.2 – это ряд измерений.
Для аналитического осмысления информации о качестве (статистических данных) часто строят гистограмму распределения.
Таблица 2
Диаметр колец
| Протокол измерения колец, мм (n=100) | |||||||||
| 3,56 | 3,46 | 3,48 | 3,50 | 3,42 | 3,43 | 3,52 | 3,49 | 3,44 | 3,50 |
| 3,48 | 3,56 | 3,50 | 3,52 | 3,47 | 3,48 | 3,46 | 3,50 | 3,56 | 3,38 |
| 3,41 | 3,37 | 3,47 | 3,49 | 3,45 | 3,44 | 3,50 | 3,49 | 3,46 | 3,46 |
| 3,55 | 3,52 | 3,44 | 3,50 | 3,45 | 3,44 | 3,48 | 3,46 | 3,52 | 3,46 |
| 3,48 | 3,32 | 3,40 | 3,52 | 3,34 | 3,46 | 3,43 | 3,30 | 3,46 | 3,52 |
| 3,59 | 3,63 | 3,59 | 3,47 | 3,38 | 3,52 | 3,45 | 3,48 | 3,31 | 3,46 |
| 3,40 | 3,54 | 3,46 | 3,51 | 3,48 | 3,50 | 3,68 | 3,60 | 3,46 | 3,52 |
| 3,48 | 3,50 | 3,56 | 3,50 | 3,52 | 3,46 | 3,48 | 3,46 | 3,52 | 3,56 |
| 3,52 | 3,48 | 3,46 | 3,45 | 3,46 | 3,54 | 3,54 | 3,48 | 3,49 | 3,41 |
| 3,41 | 3,45 | 3,34 | 3,44 | 3,47 | 3,47 | 3,41 | 3,48 | 3,54 | 3,47 |
Гистограмма – это метод представления данных, сгруппированных по частоте попадания в определенный (заранее установленный) интервал. При простоте построения гистограмма дает много полезной аналитической информации о разбросе (рассеивании) качественных показателей, средних значениях, о точности и стабильности технологических процессов, о точностных возможностях технологического оборудования. Рассмотрим пример, представленный в табл.2.
Анализ этих данных позволяет установить наименьшее и наибольшее значение измеряемого параметра Xmin = 3,3 мм, Xmax = 3,68 мм. R = Xmin – Xmax = 0,38 мм. Разбиваем диапазон распределения интересующего нас параметра качества (в данном случае диаметра колец) на равные интервалы.
Надо учесть, что при слишком большом числе интервалов картина распределения будет искажена случайными зигзагами частот, слишком малочисленных при узких интервалах. При слишком малом числе интервалов характерные особенности распределения будут сглажены. Рекомендуется брать число интервалов (l) в пределах 8–10 при числе наблюдений 100–150. Для числа наблюдений 200–300 и более оптимальное число интервалов e = (10...20).
Для нашего примера выбираем e = 9. Тогда шаг разбиения (т.е. ширина каждого интервала) будет равен:
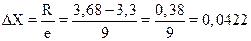 .
.
Для удобства построения назначим 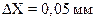 .
.
Подсчитаем теперь частоты по интервалам, расположив данные в виде табл.3.
Таблица 3
Распределение частот
| Порядковый номер интервала | Середина интервала | Границы интервала | Подсчет частот | Частота в интервале | Частость*) |
| 1 | 3,30 | 3,275 - 3,325 | III | 3 | 0,03 |
| 2 | 3,35 | 3,325 - 3,375 | III | 3 | 0,03 |
| 3 | 3,40 | 3,375 - 3,425 | | 9 | 0,09 |
| 4 | 3,45 | 3,425 - 3,475 | | 32 | 0,32 |
| 5 | 3,50 | 3,475 - 3,525 | | 38 | 0,38 |
| 6 | 3,55 | 3,525 - 3,575 | | 10 | 0,10 |
| 7 | 3,60 | 3,575 - 3,625 | III | 3 | 0,03 |
| 8 | 3,65 | 3,625 - 3,675 | I | 1 | 0,01 |
| 9 | 3,70 | 3,675 - 3,725 | I | 1
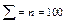
| 0,01
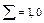
|
В столбец 4 заносят штриховые отметки, фиксирующие попадание измеренных значений (из табл.2) в интервал, указанный в столбце 3. Число штриховых отметок, т.е. частота попадания в каждый интервал, фиксируются в столбце 5.
Более наглядную картину дает графическое представление распределения частот с помощью гистограммы.
Гистограмма строится следующим образом: над каждым отрезком оси абсцисс, изображающим интервал значений, с центром в середине интервала, строится прямоугольник, высота которого пропорциональна частоте или частости в данном интервале (рис.6).

Рис.6. Гистограмма распределения:
I – нижний предел поля допуска;
II – верхний предел поля допуска
Благодаря наглядности и легкости построения гистограммы получили повсеместное применение как в области контроля качества, так и в области решения различных исследовательских проблем. В частности, метод гистограммы применяется при текущем контроле качества в процессе производства, при изучении возможностей технологических __________________________________________________
*) Частость – отношение частоты попадания в интервал к общему числу наблюдений
процессов. Гистограммы применяются для анализа работы отдельных исполнителей и станков, а также при обучении наладчиков, операторов и контролеров. Гистограммы находят широкое применение при составлении месячных отчетов цехов и заводов по качеству продукции, отчетов о результатах технического контроля, при иллюстрации изменений уровня качества по плановым периодам, а также при периодической плановой проверке точности оборудования.
КОНТРОЛЬНЫЙ ЛИСТОК
Контрольные листки используются при проведении текущего контроля заготовок, деталей, готовой продукции, сырья, полуфабрикатов и т.д.; при анализе оборудования и технологического процесса, при анализе брака и во многих других случаях. Форма листков разрабатывается в зависимости от поставленной задачи с целью сбора конкретных данных, необходимых и достаточных для решения поставленного вопроса. В предыдущем разделе показаны преимущества применения на производстве метода гистограмм. При рассмотрении практического примера прежде, чем построить гистограмму, необходимо систематизировать данные в виде таблицы (см. табл.3), которая является контрольным листком. Такие листки применяются часто при контроле готовых изделий. Рассмотрим пример: в механическом цехе обрабатывается деталь "ручка" 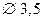 . Допуск – 0,08. Для проверки параметра применяется скоба 1271–2064. Результаты контроля приведены в табл.4 (контрольный листок).
. Допуск – 0,08. Для проверки параметра применяется скоба 1271–2064. Результаты контроля приведены в табл.4 (контрольный листок).
С помощью табл.4 устанавливается доля дефектности за каждый день и, кроме того, предусматривается расчет средней доли дефектности за месяц 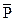 . В таблице фиксируется количество проверенных выборок K = 20. Такой контрольный листок позволяет осуществлять сбор данных за большой период времени и использовать эти данные в контрольных управляющих картах.
. В таблице фиксируется количество проверенных выборок K = 20. Такой контрольный листок позволяет осуществлять сбор данных за большой период времени и использовать эти данные в контрольных управляющих картах.
Таблица 4
Сведения о приемке детали "ручка"
| Дата (февраль 1984г.) | № п/п | Число проверенных деталей n, шт. | Число дефектных деталей X, шт. (np) | Доля дефектных деталей P, %
P= 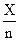 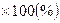
|
| 1 | 1 | 700 | 2 | 0,28 |
| 2 | 2 | 700 | 0 | 0 |
| 3 | 3 | 800 | 5 | 0,625 |
| 6 | 4 | 700 | 4 | 0,57 |
| 7 | 5 | 700 | 2 | 0,28 |
| 8 | 6 | 700 | 2 | 0,28 |
| 9 | 7 | 700 | 3 | 0,42 |
| 10 | 8 | 700 | 2 | 0,28 |
| 14 | 9 | 650 | 1 | 0,15 |
| 15 | 10 | 650 | 1 | 0,15 |
| 16 | 11 | 700 | 3 | 0,42 |
| 17 | 12 | 430 | 0 | 0 |
| 20 | 13 | 700 | 4 | 0,57 |
| 21 | 14 | 700 | 2 | 0,28 |
| 22 | 15 | 700 | 3 | 0,42 |
| 23 | 16 | 700 | 5 | 0,71 |
| 24 | 17 | 700 | 3 | 0,42 |
| 27 | 18 | 800 | 5 | 0,625 |
| 28 | 19 | 500 | 0 | 0 |
| 29 | 20 | 500 | 0 | 0 |
| Итого | К=20 | 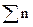 =13430 =13430
| 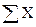 =47= =47= 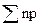
| 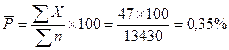
|
Аналогичный контрольный листок представлен в табл.5.
Таблица 5
| Дата (декабрь 1983г.) | Число проверенных манометров n, шт. | № п/п | Число дефектных манометров X, шт. (np) | Доля дефектных манометров P, %
P= 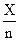 
|
| 1 | 400 | 1 | 14 | 3,5 |
| 2 | 400 | 2 | 13 | 3,2 |
| 5 | 400 | 3 | 10 | 2,5 |
| 6 | 400 | 4 | 12 | 3,0 |
| 7 | 400 | 5 | 5 | 1,2 |
| 8 | 400 | 6 | 7 | 1,7 |
| 9 | 400 | 7 | 24 | 6,0 |
| 12 | 400 | 8 | 12 | 3,0 |
| 13 | 400 | 9 | 8 | 2,0 |
| 14 | 400 | 10 | 16 | 4,0 |
| 15 | 400 | 11 | 13 | 3,2 |
| 16 | 400 | 12 | 43 | 10,7 |
| 19 | 400 | 13 | 12 | 3,0 |
| 20 | 400 | 14 | 11 | 2,7 |
| 21 | 400 | 15 | 16 | 4,0 |
| 22 | 400 | 16 | 18 | 4,5 |
| 23 | 400 | 17 | 14 | 3,5 |
| 26 | 400 | 18 | 10 | 2,5 |
| 27 | 400 | 19 | 15 | 3,7 |
| 28 | 400 | 20 | 7 | 1,7 |
| Итого | 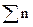 =8000 =8000
| К=20 | 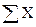 =280= =280= 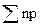
| 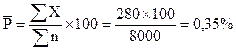
|
Контрольные листки, представленные в табл.4 и 5, фиксируют долю дефектности в %. Например, 2 декабря 1983 г. из 400 проверенных манометров – 13 дефектных, т.е. доля дефектности – 3,2%. Но при этом не фиксируется, какое число дефектов в неисправных манометрах. Дефектный прибор может иметь один, два или десять дефектов. На исправление одного дефекта потребуется намного меньше времени, чем на исправление десяти дефектов.
Когда проверяется сложная продукция часто целесообразно фиксировать число дефектов, приходящихся на единицу продукции.
Рассмотрим пример. В табл.6 приводятся результаты контроля печатных плат после металлизации. Проверено 10 партий (К = 10).
Таблица 6
Сведения о контроле печатных плат
| Дата (март 1984г.) | № п/п | Число проверенных печатных плат n, шт. | Суммарное число дефектов C в проверяемой партии | Число дефектов на единицу продукции
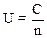
|
| 12 | 1 | 13 | 3 | 0,23 |
| 13 | 2 | 13 | 2 | 0,154 |
| 14 | 3 | 13 | 3 | 0,23 |
| 15 | 4 | 13 | 1 | 0,077 |
| 16 | 5 | 13 | 0 | 0 |
| 19 | 6 | 13 | 4 | 0,307 |
| 20 | 7 | 13 | 3 | 0,23 |
| 21 | 8 | 13 | 2 | 0,154 |
| 22 | 9 | 13 | 0 | 0 |
| 23 | 10 | 13 | 1 | 0,077 |
| Итого | К=10 | 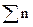 =130 =130
| 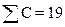
| 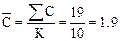
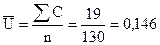
|
Контрольный листок показывает, какое суммарное число дефектов обнаружено в проверенных изделиях. Например, 19 марта 1984 г. в проверенных 13 печатных платах
(n = 13) обнаружено 4 дефекта. Число дефектов на единицу продукции U определяется формулой:
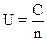 (19 марта
(19 марта 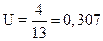 ).
).
Такой контрольный листок предусматривает сбор информации за длительный период времени и расчет средних значений 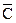 и
и  . Этот листок также позволяет на его основе применять метод контрольных карт.
. Этот листок также позволяет на его основе применять метод контрольных карт.
В табл.7 представлен контрольный листок, предназначенный для наблюдений за качеством сборки изделия A – сложного, дорогостоящего устройства, все дефекты которого подлежат исправлению. Каждый дефект связан с большими материальными и трудовыми затратами, поэтому необходимо проведение работ по уменьшению дефектности. Собрана информация о контроле 130 ед. продукции (месячный план). Количество проверяемых изделий за один рабочий день менялось от четырех до шести. Например, 2 декабря проверено 5 изделий, в которых обнаружено 14 дефектов. Число дефектов на единицу продукции за 2 декабря U= 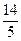 =2,8.
=2,8.
По табл. 7 можно легко установить:
- вид и число дефектов в каждой единице проверяемой продукции;
- суммарное число дефектов, обнаруженных в проверенных изделиях (за день, неделю, месяц);
- главные дефекты (за день, неделю, месяц);
- число дефектов на единицу продукции (за день, неделю, месяц);
- виновника брака.
Таблица 7
Дата: 2019-02-24, просмотров: 436.