Пусть функция 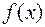 —
— 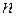 раз непрерывно дифференцируема в точке
раз непрерывно дифференцируема в точке 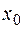 и
и 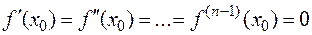 , но
, но  . Тогда:
. Тогда:
1) если 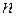 — четное и
— четное и 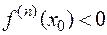 то
то 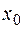 — точка локального максимума.
— точка локального максимума.
2) если 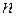 — четное и
— четное и 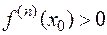 , то
, то 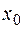 — точка локального минимума;
— точка локального минимума;
3) если 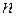 — нечетное, то
— нечетное, то 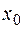 не является точкой локального экстремума.
не является точкой локального экстремума.
47) Определение выпуклой и вогнутой функции. Достаточный признак выпуклости и вогнутости.
График функции называется выпуклым в интервале 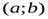 , если он расположен ниже касательной, проведенной в любой точке этого интервала (рис.3).
, если он расположен ниже касательной, проведенной в любой точке этого интервала (рис.3).
График функции называется вогнутым в интервале 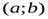 , если он расположен выше касательной, проведенной в любой точке этого интервала (рис. 4).
, если он расположен выше касательной, проведенной в любой точке этого интервала (рис. 4).

 Достаточное условие выпуклости (вогнутости).Пусть функция
Достаточное условие выпуклости (вогнутости).Пусть функция 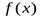 имеет вторую производную на интервале
имеет вторую производную на интервале 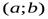 . Тогда, если
. Тогда, если 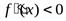 на этом интервале, то функция выпукла, если
на этом интервале, то функция выпукла, если 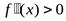 , то график функции вогнутый на этом интервале.
, то график функции вогнутый на этом интервале.
Точка графика непрерывной функции 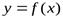 , отделяющая его части выпуклости и вогнутости, называется точкой перегиба(рис. 5).
, отделяющая его части выпуклости и вогнутости, называется точкой перегиба(рис. 5).
48)Определение точки перегиба. Необходимый признак точки перегиба.
Необходимое условие точки перегиба. Если 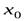 – точка перегиба функции
– точка перегиба функции 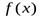 , то в этой точке вторая производная функции либо равна нулю (
, то в этой точке вторая производная функции либо равна нулю ( 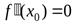 ), либо не существует.
), либо не существует.
Точки, в которых вторая производная функции равна нулю или не существует, называются критическими точками 2 –го рода.
Точки перегиба следует искать среди критических точек 2- го рода.
Первое достаточное условие точки перегиба. Пусть функция  имеет первую производную в точке
имеет первую производную в точке 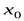 и вторую производную в некоторой окрестности этой точки (кроме, быть может самой точки). Тогда если при переходе через точку
и вторую производную в некоторой окрестности этой точки (кроме, быть может самой точки). Тогда если при переходе через точку 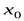 вторая производная меняет знак, то
вторая производная меняет знак, то 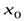 - точка перегиба.
- точка перегиба.

Второе достаточное условие точки перегиба.Пусть в точке 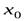 функция
функция 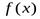 имеет производные до третьего порядка включительно. Тогда если
имеет производные до третьего порядка включительно. Тогда если 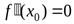 , а
, а 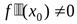 , то
, то 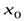 – точка перегиба этой функции.
– точка перегиба этой функции.
5. Асимптоты.
П 
 рямая линия m называется асимптотой графика функции
рямая линия m называется асимптотой графика функции 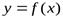 , если расстояние d от точки M, лежащей на этом графике, до прямой m стремится к нулю при неограниченном удалении этой точки по графику от начала координат в бесконечность (Рис. 6 а), б), в)).
, если расстояние d от точки M, лежащей на этом графике, до прямой m стремится к нулю при неограниченном удалении этой точки по графику от начала координат в бесконечность (Рис. 6 а), б), в)).
б
в
а
Асимптоты бывают трех видов: вертикальные (рис.6а), наклонные (рис.6б) и горизонтальные (рис.6в).
Прямая  называется вертикальной асимптотой графика функции
называется вертикальной асимптотой графика функции  , если хотя бы один из односторонних пределов
, если хотя бы один из односторонних пределов 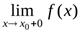 и
и  равен бесконечности.
равен бесконечности.
Обычно вертикальными асимптотами являются прямые в точках разрыва 2-го рода. Поэтому для отыскания вертикальных асимптот определяют точки 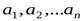 бесконечного
бесконечного
разрыва функции. Тогда уравнение вертикальных асимптот  . Вертикальные асимптоты могут быть и на границе области определения функции. Например, как у функции
. Вертикальные асимптоты могут быть и на границе области определения функции. Например, как у функции 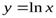 .
.
Прямая 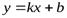 называется наклонной асимптотой графика функции
называется наклонной асимптотой графика функции 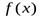 при
при 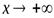 (при
(при 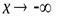 ), если
), если 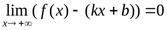 (соответственно,
(соответственно, 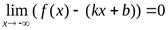 ).
).
Уравнение наклонной асимптоты к графику функции  ищем виде
ищем виде 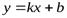 , где
, где
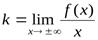 (*)
(*)
и 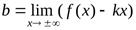 (**)
(**)
Если хотя бы один из пределов (*) и (**) не существует или равен бесконечности, то кривая 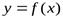 наклонной асимптоты не имеет. Асимптоты графика функции
наклонной асимптоты не имеет. Асимптоты графика функции 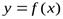 при
при  и
и 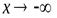 могут быть разными. Поэтому при нахождении пределов (*) и (**) следует отдельно рассматривать случай, когда
могут быть разными. Поэтому при нахождении пределов (*) и (**) следует отдельно рассматривать случай, когда 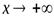 и когда
и когда 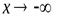 .
.
Частным случаем наклонной асимптоты (при 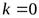 ) является горизонтальная асимптота.
) является горизонтальная асимптота.
Прямая 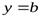 является горизонтальной асимптотой графика функции
является горизонтальной асимптотой графика функции 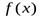 при
при 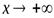 (при
(при 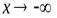 ) тогда и только тогда, когда
) тогда и только тогда, когда 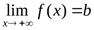 (соответственно,
(соответственно, 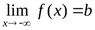 ).
).
49)Достаточные признаки точки перегиба.
Определение. Точка графика непрерывной функции f(x), при переходе через которую кривая меняет направление выпуклости, называется точкой перегиба.
Согласно определению в точке перегиба касательная к графику функции с одной стороны расположена выше [ графика, а с другой — ниже, т, e. в точке перегиба касательная пересекает кривую (см. рис. 66).
Теорема 1 (необходимое условие существования точки перегиба). Если функция у = f(x) имеет непрерывные производные до второго порядка включительно на интервале ]а; b[ и точка (х0; f (х0)), где хо  ]а;b[, является точкой перегиба графика функции f(x), то
]а;b[, является точкой перегиба графика функции f(x), то 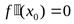
Доказательство. Так как точка (  ;f(xo)) является точкой перегиба, то слева и справа от
;f(xo)) является точкой перегиба, то слева и справа от 
 имеет разные знаки. Но тогда в силу непрерывности второй производной имеем
имеет разные знаки. Но тогда в силу непрерывности второй производной имеем 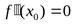 .
.
Теорема 2 (достаточное условие). Если функция y=.f(x), x  ]a; b[, дважды дифференцируема на ин-
]a; b[, дважды дифференцируема на ин-
тервале ]а; b[ и при переходе через хо 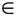 ]а; b[ вторая производная f"(x) меняет знак, то точки кривой с абсциссой х — х0 является точкой перегиба.
]а; b[ вторая производная f"(x) меняет знак, то точки кривой с абсциссой х — х0 является точкой перегиба.
Доказательство. Пусть f "(х) < 0 при 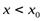 и f"(x)>0 при х > х0. Тогда при х < х0 график функции обращен выпуклостью вверх, а при х>х0 —выпуклостью вниз. Таким образом, точка (xo;f(x
и f"(x)>0 при х > х0. Тогда при х < х0 график функции обращен выпуклостью вверх, а при х>х0 —выпуклостью вниз. Таким образом, точка (xo;f(x 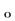 )) является точкой перегиба графика функции y=f(x).
)) является точкой перегиба графика функции y=f(x).
Аналогично доказывается, что если f"(x)>0 при х < х0 и f"(х) < 0 при х > х0, то точка (х0; f(x0)) является точкой перегиба графика функции у = f(x).
Так как вторая производная функции у = f(x) может изменить свой знак при переходе не только через точки, в которых f"(x) обращается в нуль, но и через точки, в которых 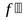 (х) не. существует, то точки перегиба следует искать среди критических точек второго рода.
(х) не. существует, то точки перегиба следует искать среди критических точек второго рода.
Пример. Найти точки перегиба графика функции
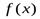 =
=  x3-2x2 + 7x-4.
x3-2x2 + 7x-4.
Решение, Данная функция определена на всей числовой прямой.
1. Находим:
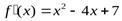 ,
, 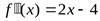
|Вторая производная 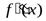 существует для любого действительного х и обращается в нуль при х = 2
существует для любого действительного х и обращается в нуль при х = 2
-критическая точка второго рода. Следовательно, на интервалах ]- 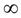 ; 2[ и ]2; +
; 2[ и ]2; + 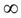 [ функцияf"(х) сохраняет свой знак.
[ функцияf"(х) сохраняет свой знак.
2. Методом пробных точек определяем знак производной f " (х) на каждом из этих интервалов. При х = 0  ]-
]- 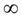 ; 2[ имеемf "(0) = -4 < 0, при х = 3
; 2[ имеемf "(0) = -4 < 0, при х = 3 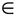 ]2; +
]2; + 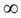 [ имеемf "(3)= 2 > 0. Следовательно, точка кривой с абсциссой х = 2 является точкой перегиба.
[ имеемf "(3)= 2 > 0. Следовательно, точка кривой с абсциссой х = 2 является точкой перегиба.
3. Находим ординату точки перегиба: у = f(2) = 4 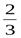 .
.
Таким образом, точка (2; 4 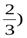 является точкой перегиба графика данной функции, причем на интервале ]-
является точкой перегиба графика данной функции, причем на интервале ]-  ; 2[ функция обращена выпуклостью вверх, а на интервале ] 2; +
; 2[ функция обращена выпуклостью вверх, а на интервале ] 2; + 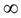 [ — выпуклостью вниз.
[ — выпуклостью вниз.
50)Определение вертикальной, горизонтальной и наклонной асимптот графика функции. Правило вычисления наклонной асимптоты.
Определение.
Асимптотой кривой называется прямая, расстояние до которой от точки, лежащей на кривой, стремится к нулю при неограниченном удалении от начала координат этой точки по кривой (рис.5.10).
Асимптоты бывают вертикальные (параллельные оси Оу), горизонтальные (параллельные оси Ох) и наклонные.
 Рис. 5.10
Рис. 5.10
Вертикальные асимптоты
Определение.
Прямая 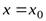 называетсявертикальной асимптотой графика функции
называетсявертикальной асимптотой графика функции 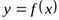 , если выполнено одно из условий:
, если выполнено одно из условий:
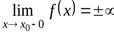 или
или 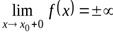 (рис.5.11)
(рис.5.11)
 Рис. 5.11
Рис. 5.11
Вертикальные асимптоты, уравнение которых х=x0 , следует искать в точках, где функция терпит разрыв второго рода, или на концах ее области определения, если концы не равны 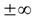 . Если таких точек нет, то нет и вертикальных асимптот.
. Если таких точек нет, то нет и вертикальных асимптот.
Например, для кривой 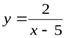 , вертикальной асимптотой будет прямая
, вертикальной асимптотой будет прямая 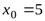 , так как
, так как 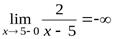 ,
, 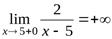 . Вертикальной асимптотой графика функции
. Вертикальной асимптотой графика функции 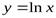 является прямая
является прямая 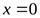 (осьОу), поскольку
(осьОу), поскольку
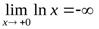 .
.
Горизонтальные асимптоты
Определение.
Если при 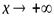 (
( 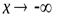 ) функция
) функция 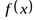 имеет конечный предел, равный числуb:
имеет конечный предел, равный числуb:
 ,
,
то прямая 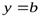 есть горизонтальная асимптота графика функции
есть горизонтальная асимптота графика функции 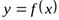 .
.
Например, для функции 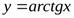 имеем
имеем
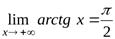 ,
, 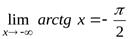 .
.
Соответственно, прямая 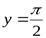 − горизонтальная асимптота для правой ветви графика функции
− горизонтальная асимптота для правой ветви графика функции 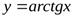 , а прямая
, а прямая 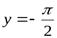 − для левой ветви.
− для левой ветви.
В том случае, если
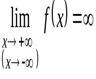 ,
,
график функции не имеет горизонтальных асимптот, но может иметь наклонные.
Наклонные асимптоты
Определение.
Прямая  называетсянаклонной асимптотой графика функции
называетсянаклонной асимптотой графика функции 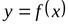 при
при 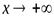 (
(  ), если выполняется равенство
), если выполняется равенство
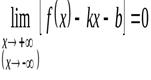 .
.
Наличие наклонной асимптоты устанавливают с помощью следующей теоремы.
Теорема.
Для того, чтобы график функции 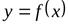 имел при
имел при 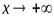 (
( 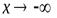 ) наклонную асимптоту
) наклонную асимптоту 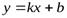 , необходимо и достаточно, чтобы существовали конечные пределы
, необходимо и достаточно, чтобы существовали конечные пределы
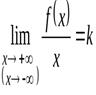 и
и 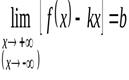 .
.
Если хотя бы один из этих пределов не существует или равен бесконечности, то кривая 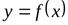 наклонной асимптоты не имеет.
наклонной асимптоты не имеет.
Замечания.
1. При отыскании асимптот следует отдельно рассматривать случаи 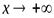 и
и 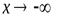 .
.
2. Если
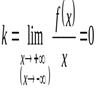 и
и  ,
,
то график функции 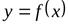 имеет горизонтальную асимптоту
имеет горизонтальную асимптоту 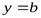 .
.
3. Если
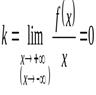 и
и 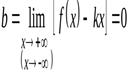 ,
,
то прямая 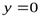 (осьОх) является горизонтальной асимптотой графика функции
(осьОх) является горизонтальной асимптотой графика функции 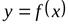 .
.
Из замечаний следует, что горизонтальную асимптоту можно рассматривать как частный случай наклонной асимптоты при 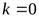 . Поэтому при отыскании асимптот графика функции рассматривают лишь два случая:
. Поэтому при отыскании асимптот графика функции рассматривают лишь два случая:
1) вертикальные асимптоты,
2) наклонные асимптоты.
Пример
Найти асимптоты графика функции  .
.
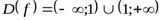 .
.
1) 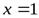 − точка разрыва второго рода:
− точка разрыва второго рода:
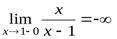 ,
, 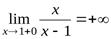 .
.
Прямая 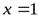 − вертикальная асимптота.
− вертикальная асимптота.
2) 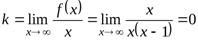 ,
,
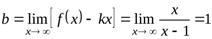 ,
,
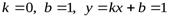 .
.
Прямая 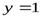 − горизонтальная асимптота. Наклонной асимптоты нет.
− горизонтальная асимптота. Наклонной асимптоты нет.
51)Основные определения функции нескольких переменных: базис в пространстве 𝑅𝑛, окрест-ность точки, открытое и замкнутое множества, область в пространстве 𝑅𝑛.
52) Область определения функции нескольких переменных, геометрический смысл, линии уровня.
Определение 1.1. Переменная z (с областью изменения Z) называется функцией двух независимых переменных х,у в множестве М, если каждой паре (х,у) из множества М по некоторому правилу или закону ставится в соответствие одно определенное значение z из Z.
Определение 1.2. Множество М, в котором заданы переменные х,у, называется областью определения функции, а сами х,у – ее аргументами.
Обозначения: z = f(x,y), z = z(x,y).
Примеры.
1. z = xy, z = x² + y² - функции, определенные для любых действительных значений х,у.
2. 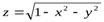 - функция, областью определения которой являются решения неравенства
- функция, областью определения которой являются решения неравенства 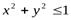 .
.
Замечание. Так как пару чисел (х,у) можно считать координатами некоторой точки на плоскости, будем впоследствии использовать термин «точка» для пары аргументов функции двух переменных, а также для упорядоченного набора чисел 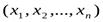 , являющихся аргументами функции нескольких переменных.
, являющихся аргументами функции нескольких переменных.
Определение 1.3. . Переменная z (с областью изменения Z) называется функцией нескольких независимых переменных  в множествеМ, если каждому набору чисел
в множествеМ, если каждому набору чисел  из множестваМ по некоторому правилу или закону ставится в соответствие одно определенное значение z из Z. Понятия аргументов и области определения вводятся так же, как для функции двух переменных.
из множестваМ по некоторому правилу или закону ставится в соответствие одно определенное значение z из Z. Понятия аргументов и области определения вводятся так же, как для функции двух переменных.
Обозначения: z = f 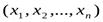 ,z = z
,z = z 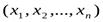 .
.
Дата: 2019-02-19, просмотров: 416.