Теорема 1. Пусть функция 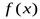имеет в точке 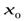производные доп-го порядка включительно. Тогда для остаточного члена имеет место равенство

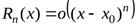при

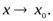
Доказательство. Прежде всего, заметим, что существование производных 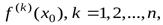означает следующее: функция 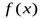имеет производные до 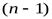-го порядка в некоторой окрестности точки 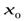, и имеет производнуюп-го порядка в самой точке .

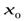Для доказательства теоремы достаточно показать, что

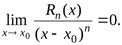
В силу соотношений (2) к этому пределу можно ( 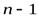) раз применить правило Бернулли–Лопиталя:

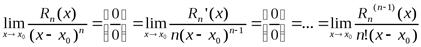
Учитывая все те же соотношения (2), последний предел можно записать как

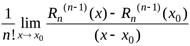
Но этот предел есть не что иное как определение производной функции 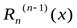в точке 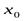, т.е. он равен 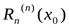. Но в силу (2) эта производная равна . Итак

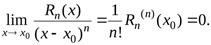
Теорема доказана.

Выпишем формулу Тейлора с учётом доказанной теоремы:

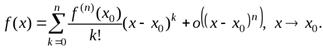(3)

Замечание 1. Форма Пеано остаточного члена полезна при использовании формулы Тейлора для вычисления пределов.

Замечание 2. Формула (3) является естественным обобщением формулы бесконечно малых приращений (тема «Производная», §4), которую можно записать так: 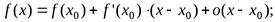она получается из (3) прип = 1.

Формула Тейлора с остаточным членом в форме Лагранжа

Теорема 2. Пусть функция 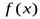имеет в некотором промежутке, содержащем точку 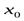, производные до 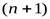-гопорядка включительно. Тогда для любого 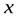из этого промежутка найдётся точка 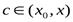такая, что

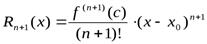
Замечание 1. Форма Лагранжа остаточного члена используется в тех случаях, когда требуется приближённо вычислить 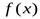при фиксированном значении 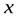, отличном от 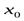. Остаточный член в этой форме напоминает следующий, очередной, член формулы Тейлора, лишь только вычисляется не в точке 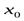, а в некоторой точке между и .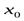

Выпишем формулу Тейлора с учётом теоремы 2:

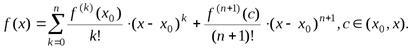
43)Формула Маклорена для функций 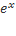,sin x, cos x, 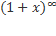,ln(1+x)

Тетрадь

44)Теорема о необходимых и достаточных условиях возрастания и убывания функции

Необходимые условия возрастания (убывания) функции.

Теорема 32. Если дифференцируемая на некотором интервале 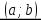функция 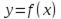возрастает (убывает) на нем, то ( 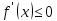) для всех .

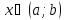Доказательство. Пусть функция 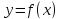возрастаетинтервале 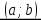. Выберем произвольные точк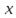и и 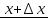на этом интервале и рассмотрим отношение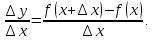

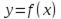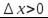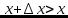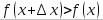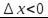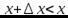Функция возрастает, поэтому при будет и , а при будет и 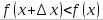. В обоих случаях

так как числитель и знаменатель дроби будут иметь одинаковые знаки.

Следовательно,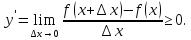

Аналогично рассматривается случай, когда функция убывает наинтервале .

Замечание 1. Геометрически теорема 32 означает, что касательные к графику возрастающей функции имеют острые углы с положительным направлением оси (рис. 62), а убывающие – тупые (рис. 63).