Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

1. Алгебраическая сумма конечного числа б.м.ф. есть б.м.ф.

2. Произведение б.м.ф. на ограниченную функцию есть б.м.ф. (в том числе на постоянную или на другую б.м.ф.).

3. Частное от деления б.м.ф., предел которой отличен от 0, есть б.м.ф.

Функция y=f(x)называетсябесконечно большой(илибесконечно большой величиной) при 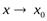, если 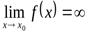. Например, 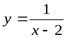б.б.ф. при 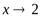, т.к.f(x)→ ∞ илиy=tgxприх 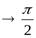б.б.ф.

Аналогично определяется б.б.ф. при х→±∞, 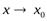+ и -.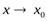

Если f(x) → ∞ при 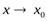и принимает лишь положительные значения, то пишут , если лишь отрицательные, то .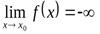

Свойства бесконечно больших функций:

1. Произведение б.б.ф. на функцию, предел которой отличен от 0, есть б.б.ф.

2. Сумма б.б.ф. и ограниченной функции есть б.б.ф.

3. Частное от деления б.б.ф. на функцию, имеющую предел, есть б.б.ф.

11

Связь между бесконечно малыми и бесконечно большими функциями

Теорема:Если функция α (х) – бесконечно малая при , то

функция 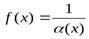является бесконечно большой при

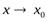, и наоборот.

 

19) Первый замечательный предел.

Первый замечательный предел:

 

 

Доказательство

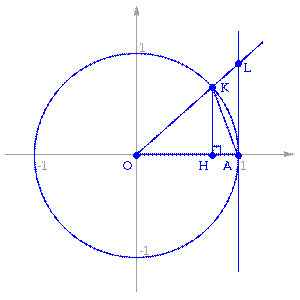
Рассмотрим односторонние пределы 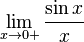и 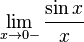и докажем, что они равны 1.

Пусть . Отложим этот угол на единичной окружности ( ).

Точка K— точка пересечения луча с окружностью, а точкаL— с касательной к единичной окружности в точке . ТочкаH— проекция точкиKна осьOX.

Очевидно, что:

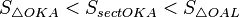(1)

(где 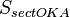— площадь сектора )

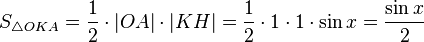
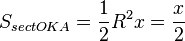
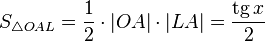
(из : )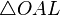

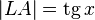Подставляя в (1), получим:

Так как при :

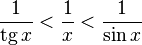
Умножаем на :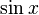

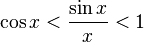
Перейдём к пределу:

Найдём левый односторонний предел:

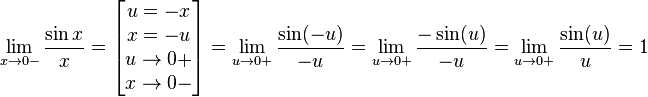
Правый и левый односторонний пределы существуют и равны 1, а значит и сам предел равен 1.

 

20) Второй замечательный предел :

Доказательство второго замечательного предела:

Доказательство для натуральных значений x [показать]

Зная, что второй замечательный предел верен для натуральных значений x, докажем второй замечательный предел для вещественных x, то есть докажем, что 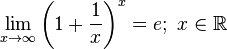. Рассмотрим два случая:

1. Пусть . Каждое значение x заключено между двумя положительными целыми числами: 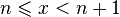, где 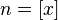— это целая часть x.

Отсюда следует: , поэтому

.

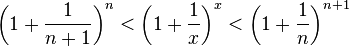Если , то 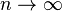. Поэтому, согласно пределу , имеем:

.

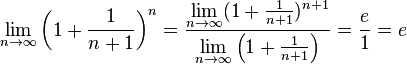
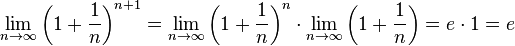По признаку (о пределе промежуточной функции) существования пределов .

2. Пусть . Сделаем подстановку 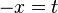, тогда

.

Из двух этих случаев вытекает, что 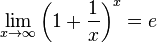для вещественного x.

 

21) Сравнение бесконечно малых функций, пример

 

22) Свойства эквивалентных бесконечно малых.

Как известно, сумма, разность и произведение двух б.м.ф. есть функция бесконечно малая. Отношение же двух б.м.ф. может вести себя различным образом: быть конечным числом, быть бесконечно большой, бесконечно малой функцией или вообще не стремиться ни к какому пределу.

Две б.м.ф. сравниваются между собой с помощью их отношения.

Пусть 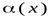и есть б.м.ф. при 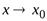, т.е. 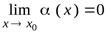и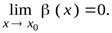

1. Если 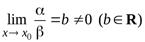, то называютсябесконечно малыми одного порядка.

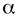2. Если , то называетсябесконечно малой более высокого порядка, чем β.

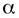3. Если , то называетсябесконечно малой более низкого порядка, чем β.

4. Если 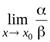не существует, то 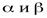называютсянесравнимыми бесконечно малыми.

 

Пример Сравнить порядок функций при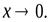

Решение. При это б.м.ф. одного порядка, так как

Говорят, что б.м.ф. 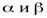одного порядка стремятся к нулю с примерно одинаковой скоростью.

Пример Являются ли функции б.м.ф. одного порядка при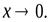

Решение. При 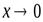функция 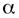есть б.м.ф. более высокого порядка, чем β, так как 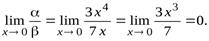В этом случае б.м.ф. 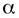стремится к нулю быстрее, чем β.

Пример Сравнить порядок функци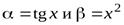й при .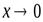

Решение. Так как то 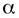есть б.м.ф. более низкого порядка, чем β.

Пример Можно ли сравнить функци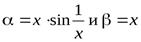и при ?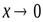

 

23)Определения функции, непрерывной в точке. Их эквивалентность. Примеры.

Функция f(x) называется непрерывной в точке x₀, если она определена на некоторой окрестности U(x₀) этой точки, и если предел при x стремящемся к x₀ существует и равен значению функции в x₀: .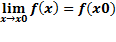

Здесь подразумевается, что x0 – это конечная точка. Значение функции в ней может быть только конечным числом.

Если привлечь сюда определение конечного предела функции в конечной точке, то можно дать развернутую формулировку определения непрерывности функции. Поскольку имеется два равносильных определения предела функции (по Коши и по Гейне), то можно дать, как минимум, еще два эквивалентных определения непрерывности.

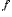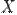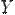Соответствие между элементами множеств и называетсяфункцией, еслилюбомуэлементу поставлен в соответствиеединственныйэлемент (это записывается следующим образом: 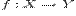или ).

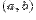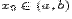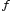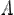Определение предела функции по Гейне.Пусть в каждой точке интервала , кроме, быть может, точки , определена функция Число называетсяпределомфункции 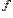при стремлении 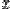к 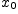, если для любой последовательности 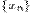такой, что последовательность 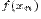значений функции 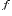сходится к 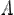при .В этом случае пишут

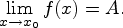
Пример. Пусть

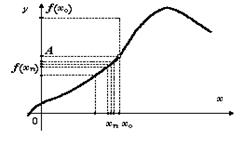
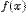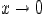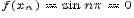Предел функции при не существует, так как для значения функции , а для ,

.

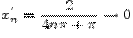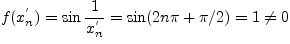Пример.Пусть Тогда 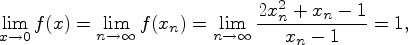так как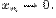

Определение предела функции по Коши.Пусть в каждой точке интервала 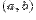, кроме, быть может, точки 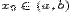, определена функция 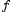. Число 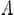называетсяпределомфункции 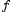при стремлении 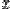к 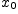, если для любого 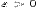существует 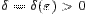такое, что для всех 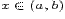, удовлетворяющих условию , выполняется неравенство 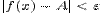. Или, на формальном языке,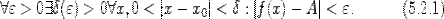

24)Локальные свойства функций, непрерывных в точке.

Локальными называют такие свойства функций, которые определяются поведением функции в сколь угодно малой окрестности точки области определения.

Теорема (формулировка)

Пусть f:E→R — функция, непрерывная в точке x0∈R тогда справедливы следующие утверждения:

· Функция f ограничена в некоторой окрестности UE(x0).

· Если f(x0)≠0, то в некоторой окрестности UE(x0) точки x0 функция f(x)>0
( или f(x)<0 ) вместе с f(x0).

· Если функция g:UE(x0) →R также непрерывна в точке x0, то следующие функции непрерывны в точке x0:

§ f+g

§ f⋅g

§ f/g

Если функция g:Y →R непрерывна в точке y0∈Y, а функция f такова, что f:E →R, f(x0)=y0, f(E)∈Y и f непрерывна в точке x0, то композиция g∘f непрерывна в точке x0.

Пример 1

Алгебраический многочлен Pn(x)=a0xn+a1xn−1+…+an является непрерывной функцией для x∈R. Это следует из теоремы 1 и непрерывности функции y=x и y=k.

Пример 2

Рациональная функция R(x)=Pn(x)Qm(x) непрерывна всюду, кроме точек, в которых Qm(x)=0.

25)Определение функции, непрерывной на отрезке. Непрерывность элементарных функций и до-казательство для y=sin(x)

Функция, непрерывная во всех точках некоторой области, называется непрерывной в этой области.

Функция называется непрерывной справа в точке , если .

Функция называется непрерывной слева в точке , если .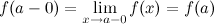

Функция 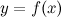называется непрерывной в интервале 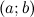, если она непрерывна в каждой точке этого интервала.

Функция 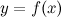называется непрерывной на отрезке 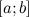, если она является непрерывной в интервале 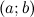, непрерывной справа в точке , то есть 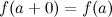и непрерывной слева в точке 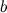, то есть .

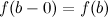Функция y = sin x

При вычислении предела 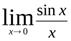было установлено, что если 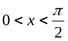, то 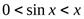. Ввиду нечетности функцийy=x и y= sin x, при 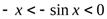. Из этого сразу следует, что при 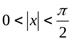выполняется неравенство . Пустьx₀ произвольная точка. Докажем, что 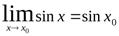. Это равносильно тому, что . В свою очередь, это равносильно тому, что 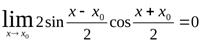. Так как, по доказанному выше, 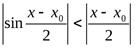, 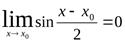. Кроме того, функция 2cos 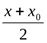, очевидно, ограниченная. По свойствам бесконечно малых, получаем требуемое

 

26Глобальные свойства непрерывных функций (теоремы Больцано-Коши и Вейершрасса).)