1. Устранимый разрыв.

Точка а называется точкой устранимого разрыва функции 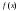, если предел функции в этой точке существует, но в точке а функция 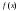либо не определена, либо ее значение 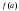не равно пределу в этой точке

2. Разрыв первого рода.

Точка а называется точкой разрыва первого рода функции 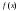, если в этой точке функция имеет конечные, но не равные друг другу левый и правый пределы.

3. Разрыв второго рода.

Точка а называется точкой разрыва второго рода функции Точка а называется точкой устранимого разрыва функции 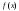, если в этой точке функция не имеет по крайней мере одного из односторонних пределов или хотя бы один из односторонних пределов бесконечен.

28) Определение производной функции в точке. Односторонние производные. Примеры функций, не имеющих производной в точке.

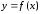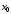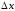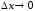ОПРЕДЕЛЕНИЕ. Производной функции в точке называется предел отношения приращения функции в этой точке к приращению аргумента , при (если этот предел существует и конечен), т.е.

.

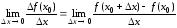Обозначают: , , , .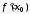

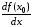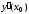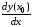Производной функции 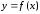в точке 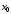справа (слева) называется

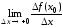
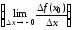
(если этот предел существует и конечен).

Обозначают: 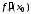, 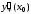– производная 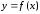в точке справа,

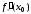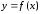, – производная в точке 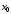слева.

Очевидно, что справедлива следующая теорема.

ТЕОРЕМА. Функция 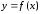имеет производную в точке 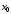тогда и только тогда, когда в этой точке существуют и равны между собой производные функции справа и слева. Причем

.

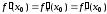Следующая теорема устанавливает связь между существованием производной функции в точке 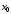и непрерывностью функции в этой точке.

ТЕОРЕМА (необходимое условие существования производной функции в точке). Если функция 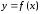имеет производную в точке 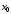, то функция 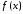в этой точке непрерывна.

Односторонние производные

Введем понятия левой и правой производных функции 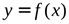по аналогии с понятием левого и правого предела.

ОПРЕДЕЛЕНИЕ. Правой производной функции 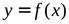в точке 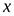называется при условии, что этот предел существует.

То, что 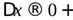означает, что , то есть при вычислении правой производной 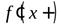к точке приближаются справа.

ОПРЕДЕЛЕНИЕ. Левой производной функции 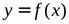в точке 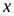называется при условии, что этот предел существует.

При вычислении левой производной полагается .

Имеют место утверждения:

1. если функция имеет в точке 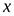производную 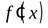, то она имеет в этой точке как левую, так и правую производные, причем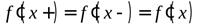

2. если функция имеет в точке 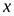как правую, так и левую производные, причем эти производные равны между собой, то в точке 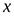существует производная, причем .

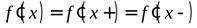3. если 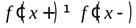, то в точке 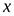функция не имеет производной.

ПРИМЕР. Рассмотрим функцию .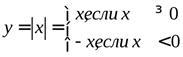

Вычислим односторонние производные (правую и левую) в точке .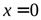

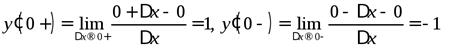. Односторонние производные неравны, значит, 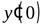не существует. В других точках эта функция производную имеет.

Примеры функций, не имеющих производную.

1) f(x)=sign x=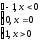

В точке х₀=0 нет производной

f(0+Dx)-f(0)=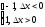

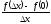= - нет предела приDх→0

2) f(x)= ê х ê - в точке х₀=0 нет производной (в положительной полуплоскости f¢(x)=х, в отрицательной - f¢(x)=-х). (График)

f(0+Dx)-f(0)= 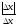, , 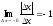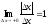Þ нет предела при Dх→0

29) Физический и геометрический смыслы производной. Уравнение касательной и нормали к кривой.

1) Физический смысл производной. Если функция 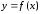и ее аргумент являются физическими величинами, то производная 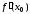– скорость изменения переменной относительно переменной в точке 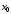. Например, если 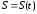– расстояние, проходимое точкой за время 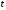, то ее производная – скорость в момент времени 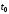. Если – количество электричества, протекающее через поперечное сечение проводника в момент времени 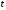, то 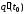– скорость изменения количества электричества в момент времени 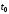, т.е. сила тока в момент времени .

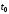2) Геометрический смысл производной.

Пусть 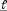– некоторая кривая, 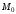– точка на кривой .

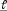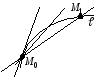
Любая прямая, пересекающая 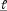не менее чем в двух точках называетсясекущей.

УРАВНЕНИЯ КАСАТЕЛЬНОЙ И НОРМАЛИ

Уравнение касательной

Пусть функция задается уравнением y=f(x), нужно написать уравнение касательной в точке x0. Из определения производной:

y/(x)=limΔx→0ΔyΔx

Δy=f(x+Δx)−f(x).

Уравнение касательной к графику функции: y=kx+b (k,b=const). Из геометрического смысла производной: f/(x0)=tgα=k Т.к. x0 и f(x0)∈ прямой, то уравнение касательной записывается в виде: y−f(x0)=f/(x0)(x−x0) , или

y=f/(x0)·x+f(x0)−f/(x0)·x0.

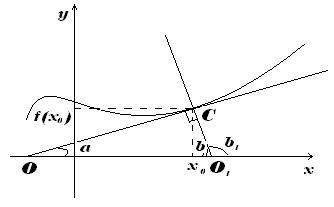
Уравнение нормали

Нормаль - это перпендикуляр к касательной (см. рисунок). Исходя из этого:

tgβ=tg(2π−α)=ctgα=1tgα=1f/(x0)

Т.к. угол наклона нормали -- это угол β1, то имеем:

tgβ1=tg(π−β)=−tgβ=−1f/(x).

Точка (x0,f(x0))∈ нормали, уравнение примет вид:

y−f(x0)=−1f/(x0)(x−x0).

30)Определение дифференцируемости функции в точке. Теоремы о связи дифференцируемости и существовании конечной производной, дифференцируемости и непрерывности.

Дифференцируемость функции в точке

Пусть функция y=f(x) определена на интервале (a,b), x-некоторая фиксированное значение аргумента из указанного интервала, 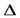x-любое приращение аргумента.

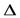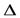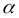
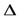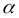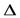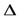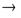Опр. Функция y=f(x) называется дифференцируемой в данной точке x, если приращение y этой функции в точке x, соответствующее приращению аргумента x, может быть представлено в виде y=A x + x, где А - некоторое число, не зависящее от x, а - функция аргумента x, является бесконечно малой при x 0.

Связь между дифференцируемостью и непрерывностью функции.

Докажем теорему, устанавливающую связь между дифференцируемостью и непрерывностью функции.

Теорема 7.1. Если функцияy=f(x) дифференцируема в произвольной точкеx₀, то она непрерывна в этой точке.

Доказательство. Пусть функция y=f(x) дифференцируема в произвольной точкеx₀, т.е. имеет в этой точке производную 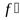(x₀). Запишем приращение функции∆yточкеx₀:

∆y= 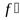(x₀) ∆ x+ 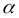∆ x, где 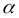→0 при ∆ x→0 (см. доказательство теоремы 6.1).

Пусть теперь ∆ x→0. Тогда, очевидно, и∆y→0. Но это и означает, что функцияy=f(x)непрерывна в точкеx₀. Теорема доказана.

Утверждение, обратное этой теореме, неверно: из непрерывности функции в данной точке не вытекает её дифференцируемость в этой точке. Существуют функции, непрерывные в некоторой точке, но не имеющие в этой точке производной. Примером такой функции служит функция

y= =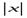

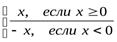
(см. рис.4).

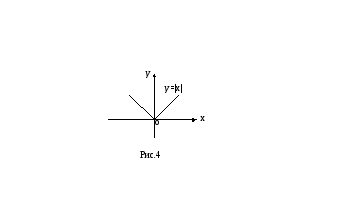
Эта функция непрерывна в точке x= 0, но не дифференцируема в ней. Действительно, приращение этой функции в точкеx= 0 есть

∆y=f(0+∆ x) ─ f(0) =f(∆ x) = ,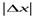

= = ,

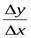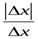т.е. в любой сколь угодно малой окрестности значения 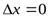отношение 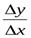принимает два различных значения: 1 и ─1. Это означает, что предел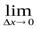 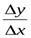не существует, т.е. функцияy= 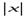не имеет производной в точкеx= 0, а, следовательно, график функции не имеет касательной в точкеO(0;0) (поскольку угловой коэффициент касательной должен быть равен производной, но производной не существует).

31)Формулы производных постоянной, суммы, произведения и частного функций.