Рассмотрим некоторые теоремы.
Теорема 1. Производная постоянной равна нулю, то есть
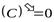 , где C-const.
, где C-const.
Теорема 2. Производная алгебраической суммы конечного числа дифференцируемых функций равна алгебраической сумме производных этих функций
 . (5)
. (5)
Теорема 3. Производная произведения дифференцируемых функций равна
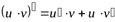 . (6)
. (6)
Следствие. Постоянный множитель можно выносить за знак производной
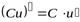 .
.
Замечание. Аналогично можно доказать формулу для произведения трех функций
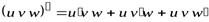 .
.
Теорема 4. Производная частного двух дифференцируемых функций равна
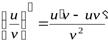 . (7)
. (7)
Замечание. Для функции вида  , гдеC-const , рациональнее применять формулу производной произведения, а не частного:
, гдеC-const , рациональнее применять формулу производной произведения, а не частного:
32) Теоремы о производных обратной и сложной функций.
Теорема о производной сложной функции
Пусть дана сложная функция 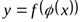 или
или 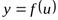 , где
, где 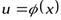 так называемый промежуточный аргумент. Справедливо правило дифференцирования сложной функции.
так называемый промежуточный аргумент. Справедливо правило дифференцирования сложной функции.
Теорема. Если функция 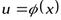 в некоторой точкех имеет производную
в некоторой точкех имеет производную 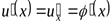 , а функция
, а функция 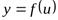 при соответствующем значенииu имеет производную
при соответствующем значенииu имеет производную 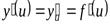 , то сложная функция
, то сложная функция 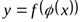 в указанной точкех также имеет производную
в указанной точкех также имеет производную 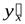 , которая равна произведению производной данной функции по промежуточному аргументу на производную промежуточного аргумента пох :
, которая равна произведению производной данной функции по промежуточному аргументу на производную промежуточного аргумента пох :
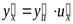 . (8)
. (8)
Сводная таблица основных формул дифференцирования
1. 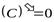 . 2.
. 2.  ,
,  ,
, 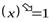 ,
, 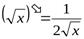 .
.
3. 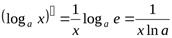 ,
, 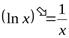 . 4.
. 4. 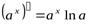 ,
, 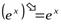 .
.
5. 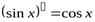 . 6.
. 6. 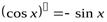 7.
7. 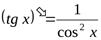 .
.
8. 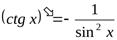 . 9.
. 9.  . 10.
. 10. 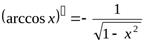 .
.
11.  . 12.
. 12. 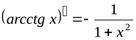 .
.
Теорема. Если функция  дифференцируема, имеет обратную функцию и
дифференцируема, имеет обратную функцию и 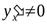 , то производная обратной функции существует и равна обратной величине производной данной функции, то есть
, то производная обратной функции существует и равна обратной величине производной данной функции, то есть
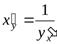 или
или  .
.
33)Формулы дифференцирования основных элементарных функций. Привести доказательство для
y=cos x, y= 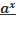 , y=arcsin x
, y=arcsin x
В тетради 
34)Определение дифференциала, его геометрический смысл. Теорема об эквивалентности диффе-ренциала и приращения функции, её применение к приближённым вычислениям. Свойство инвариантности дифференциала.
Определение. Дифференциалом функции в некоторой точке x называется главная, линейная часть приращения функции.
Дифференциал функции y = f(x) равен произведению её производной на приращение независимой переменной x (аргумента).
Приближенное выражение приращения функции через дифференциал.
Если функция  дифференцируема в точке
дифференцируема в точке 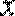 , то на основании формулы (1) ее приращение, соответствующее приращению
, то на основании формулы (1) ее приращение, соответствующее приращению 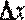 , можно записать следующим образом:
, можно записать следующим образом:
 .
.
Отсюда следует, что дифференциал функции при достаточно малых 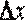 может служить хорошим приближением приращения функции. В этом смысле пишут приближенное равенство
может служить хорошим приближением приращения функции. В этом смысле пишут приближенное равенство
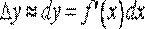 , (7)
, (7)
Которым широко пользуются.
Пусть надо вычислить значение функции 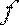 в точке
в точке 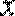 , т. е. число
, т. е. число  . Однако появилась необходимость заменить
. Однако появилась необходимость заменить 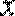 его приближенным значением
его приближенным значением 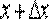 :
:
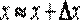 .
.
Дата: 2019-02-19, просмотров: 363.