Пусть зависимость между аргументом х и функцией у задана параметрически в виде двух уравнений

где t — вспомогательная переменная, называемая параметром.
Найдем производную у'х, считая, что функции (21.1) имеют производные и что функция х=x(t) имеет обратную t=φ(х). По правилу дифференцирования обратной функции

Функцию у=ƒ(х), определяемую параметрическими уравнениями (21.1), можно рассматривать как сложную функцию у=y(t), где t=φ(х). По правилу дифференцирования сложной функции имеем: у'х=y't•t'x. С учетом равенства (21.2) получаем
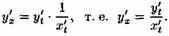
Полученная формула позволяет находить производную у'х от функции заданной параметрически, не находя непосредственной зависимости у от х.
<< Пример 21.2
Пусть 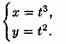
Найти у'х.

Решение: Имеем x't=3t2, y't=2t. Следовательно, у'х=2t/t2, т. е. 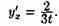
В этом можно убедиться, найдя непосредственно зависимость у от х.
Действительно, 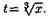 Тогда
Тогда 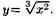 Отсюда
Отсюда  т. е.
т. е. 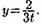
36) Определение производных и дифференциалов высших порядков. Примеры. Формула Лейбни-ца. Производные высших порядков от функций, заданных параметрически.
Пусть у =f (х) дифференцируемая функция, а её аргументх- независимая переменная. Тогда её первый дифференциалdy = f′ (x)dx есть также функция отх; можно найти дифференциал этой функции.
Дифференциал от дифференциала функции у =f (х) называется еёвторым дифференциалом (илидифференциалом второго порядка) и обозначаетсяd 2y илиd 2 f (x):
d 2 y = f′′ (x) dx2
Здесь dx 2 обозначает (dx)2.
Аналогично определяется и находится дифференциал третьего порядка: d 3 y = d (d2 y) = d (f′′ (x) dx2) = f′′′ (x) dx3.
Вообще, дифференциал n-гопорядка есть дифференциал от дифференциала(n-1)-гопорядка:d n y = d (d n - 1y) =f (n) (x) (dx)n.
Отсюда находим, что f (n(x)= d n y . В частности, приn = 1, 2, 3 соответственно получаем:dxn
| f ′(x)= | dy | , | f ′′(x)= | d 2 y | , | f ′′′(x)= | d 3 y | , т.е. производную функции можно рассматривать как |
| dx | dx2 | dx3 |
отношение её дифференциала соответствующего порядка к соответствующей степени дифференциала независимой переменной.
Отметим, что все приведённые выше формулы справедливы только, если х – независимая переменная.
Пример. Найти d 2 y, еслиy = e 3x их – независимая переменная.Решение: так какy′ = 3e 3x,y′′ = 9e 3x, то имеемd 2y = 9e 3x dx 2.
Производные высших порядков. Формула Лейбница.
Пусть функция y=f(x) дифференцируема в точке Xo, то есть существует ее производная в этой точке f ’ (Xo). Пусть f - дифференцируема в некоторой окрестности U(Xo). f’(x) определена на U(Xo) и если дифференцируема в точке Xo, то (f’(Xo))’=f’’(Xo). Вообще 
Теорема: (Формула Лейбница)
Пусть функции U и V n раз дифференцируемы, т.е. существуют  и
и 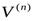 . Значит (U*V) – тоже n раз дифференцируема, при этом
. Значит (U*V) – тоже n раз дифференцируема, при этом
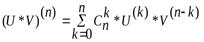
Доказательство:
Метод математической индукции:
Пусть при n=m – верно, т.е.
 (*)
(*)
Надо доказать, что
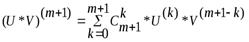
Доказательство:

Теорема доказана.
37) Теорема Ферма о дифференцируемой функции.
Теорема. Пусть функция 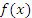 определена в некотором промежутке; имеет локальный экстремум во внутренней точке
определена в некотором промежутке; имеет локальный экстремум во внутренней точке  этого промежутка; дифференцируема в окрестности точки
этого промежутка; дифференцируема в окрестности точки  . Если
. Если  – точка локального максимума, то при переходе через эту точку производная
– точка локального максимума, то при переходе через эту точку производная 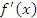 меняет свой знак с плюса на минус:
меняет свой знак с плюса на минус:
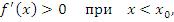 
| (10) |
Если  – точка локального минимума, то при переходе через точку
– точка локального минимума, то при переходе через точку  производная
производная  меняет свой знак с минуса на плюс:
меняет свой знак с минуса на плюс:
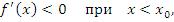 
| (11) |
Если функция 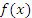 дифференцируема в точке
дифференцируема в точке  , то
, то
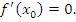
| (12) |
Доказательство. Предположим, что  является точкой локального максимума функции
является точкой локального максимума функции 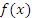 . Тогда эта функция является возрастающей для значений x, расположенных на малых расстояниях слева от точки
. Тогда эта функция является возрастающей для значений x, расположенных на малых расстояниях слева от точки  и, следовательно,
и, следовательно, 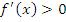 при
при 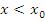 .
.
Поскольку функция 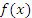 является убывающей для значений x, достаточно близких к точке
является убывающей для значений x, достаточно близких к точке  и расположенных справа, то
и расположенных справа, то 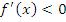 при
при 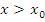 . Таким образом, утверждение (10) доказано. Аналогичным образом устанавливается справедливость утверждения (11).
. Таким образом, утверждение (10) доказано. Аналогичным образом устанавливается справедливость утверждения (11).
Теперь предположим, что функция 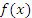 дифференцируема в точке
дифференцируема в точке  и
и 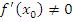 . Поскольку функция
. Поскольку функция 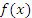 имеет экстремум в точке
имеет экстремум в точке  , то справа и слева от точки
, то справа и слева от точки  разность
разность 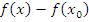 принимает значения противоположных знаков. Если
принимает значения противоположных знаков. Если 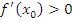 , то функция
, то функция 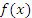 возрастает в окрестности точки
возрастает в окрестности точки  ; если
; если 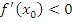 , то функция
, то функция 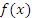 убывает в окрестности точки
убывает в окрестности точки  . В обоих случаях
. В обоих случаях  не является точкой экстремума и, таким образом, допущение
не является точкой экстремума и, таким образом, допущение 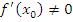 приводит к противоречию с условиями теоремы.
приводит к противоречию с условиями теоремы.
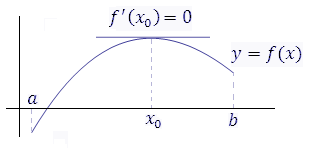
Рис. 1. Касательная к графику функции  в точке экстремума параллельна оси 0x.
в точке экстремума параллельна оси 0x.
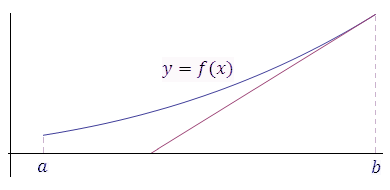
Рис. 2. Если функция принимает свое наибольшее (или наименьшее) значение не во внутренней точке промежутка, а на одном из его концов, то производная этой функции в точке экстремума не обязательно равна нулю.
38) Теорема Ролля и её геометрический смысл.
Функция у = f (x) непрерывна на отрезке [a;b] . В силу второй теоремы
Вейерштрасса она на этом отрезке принимает наименьшее и наибольшее значения. Пусть это будут значения m иM. Могут представиться два случая:
| 1) | M = m . В этом случае | m ≤ f (x)≤ m , функция | у = f(x) | является | |
| постоянной на отрезке | [a;b] . Поэтомуf '(x)= 0 во всем интервале (a;b) , | ||||
| теорема верна. | |||||
| 2) | M > m . Тогда для функцииу = f (x) даже в том крайнем случае, когда, | ||||
| например, наибольшее | значение | функции принимается | на конце | отрезка | |
f (a)= f (b)= M , наименьшее значение будет приниматься уже внутри отрезка. Следовательно, найдется точкаx0 (a;b) , в которойf (x0 )= m .
Но тогда по теореме Ферма f ′(x0 )= 0.
Теорема Ролля имеет простой геометрический смысл: найдется хотя бы одна точка, в которой касательная к графику функции будет параллельна оси абсцисс.
Если f (a)= f (b)= 0, то теорему Ролля можно сформулировать так:
между двумя последовательными нулями дифференцируемой функции имеется хотя бы один нуль производной.
39)Теорема Лагранжа о конечных приращениях и её геометрический смысл.
Пусть функция y = f(x) :
1)непрерывна на отрезке [a;b];
2)дифференцируемана интервале (a;b) .
Тогда на интервале (a;b) найдется по крайней мере одна точка x0 такая, что
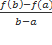 =
= 
Эта функция на [a;b] удовлетворяет условиям теоремы Ролля:
1)она непрерывна на [a;b] , поскольку непрерывны все слагаемыеL(x) ;
2)на (a;b) функцияL(x) имеет производную;
3)L(a)= L(b)= 0 .
Из теоремы Ролля следует, что существует точка x0 (a;b) , в которой
L′(x0 )= 0 .
Следовательно, L′(x0 )= f ′(x0 )- 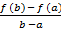 =0
=0
Отсюда f ′(x0 )= 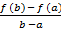 ,b x0 (a;b) .
,b x0 (a;b) .
Дата: 2019-02-19, просмотров: 363.