Если дифференцируемая функция 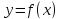 имеет экстремум в точке
имеет экстремум в точке 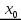 , то ее производная в этой точке равна нулю,
, то ее производная в этой точке равна нулю, 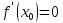 .
.
Доказательство. Пусть 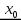 – точка максимума. Следовательно, в окрестности точки
– точка максимума. Следовательно, в окрестности точки 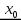 выполняется неравенство
выполняется неравенство  . Тогда
. Тогда 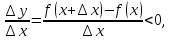 если
если 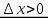 и
и
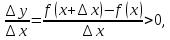
Если 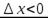 . По условию теоремы производная функции
. По условию теоремы производная функции 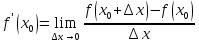
существует. Переходя к пределу при  , получим
, получим 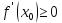 , если
, если 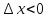 и
и  , если
, если 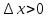 . Это возможно лишь в случае
. Это возможно лишь в случае  .
.
Аналогично можно показать утверждение теоремы если 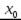 – точка минимума.
– точка минимума.
Замечание 1. Геометрически утверждение теоремы означает, что в точках экстремума касательные к графику функции параллельны оси 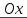 (рис. 65). Обратная теорема не верна. Если
(рис. 65). Обратная теорема не верна. Если  , то это не всегда означает, что точка
, то это не всегда означает, что точка 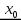 – точка экстремума. Действительно, для функции
– точка экстремума. Действительно, для функции 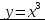 в точке
в точке 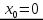 производная
производная 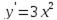 ,
, 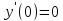 , но точка
, но точка 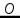 не является ни минимумом, ни максимумом (рис. 66). Существуют так же функции, которые в точках экстремума не имеют производных. Так функция
не является ни минимумом, ни максимумом (рис. 66). Существуют так же функции, которые в точках экстремума не имеют производных. Так функция  в точке
в точке 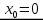 не имеет производной, но эта точка является ее минимумом (рис. 67).
не имеет производной, но эта точка является ее минимумом (рис. 67). 


Достаточное условие экстремума.
Теорема 35. Если непрерывная функция 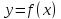 дифференцируема в некоторой
дифференцируема в некоторой 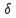 – окрестности критической точки
– окрестности критической точки 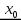 и при переходе через нее (слева направо) производная
и при переходе через нее (слева направо) производная 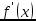 меняет знак с плюса на минус (с минуса на плюс), то точка
меняет знак с плюса на минус (с минуса на плюс), то точка 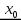 есть точка максимума (минимума).
есть точка максимума (минимума).
Доказательство. Рассмотрим 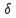 – окрестность точки
– окрестность точки  . Пусть выполняется условия:
. Пусть выполняется условия:  , для любого
, для любого 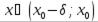 и
и 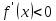 , для любого
, для любого 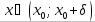 . Тогда функция
. Тогда функция 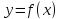 возрастает на интервале
возрастает на интервале
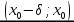 и убывает на интервале
и убывает на интервале 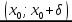 . Следовательно, значение функции
. Следовательно, значение функции 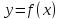 в точке
в точке 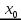 является наибольшим значением на интервале
является наибольшим значением на интервале  , т. е.
, т. е. 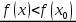 для всех
для всех 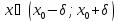 . Это означает, что
. Это означает, что 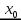 – точка максимума. Аналогично доказывается случай для точки минимума (рис. 68).
– точка максимума. Аналогично доказывается случай для точки минимума (рис. 68). 
Теорема 36. Если в точке 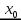 первая производная функции равна нулю
первая производная функции равна нулю 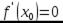 , а вторая производная в точке
, а вторая производная в точке 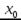 существует и отлична от нуля
существует и отлична от нуля 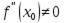 , то при
, то при 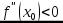 в точке
в точке 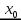 функция
функция 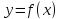 имеет максимум, а при
имеет максимум, а при 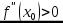 – минимум.
– минимум.
Доказательство. Пусть 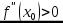 . Так как
. Так как
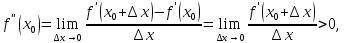
то в достаточно малой окрестности точки 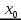 выполняется неравенство
выполняется неравенство
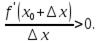
Если 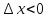 , то
, то 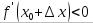 , а если
, а если 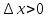 , то
, то 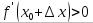 .
.
46) Второй и третий достаточные признаки экстремума.
Если функция 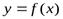 дважды дифференцируема и в некоторой точке
дважды дифференцируема и в некоторой точке 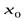 выполняются условия
выполняются условия 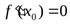 , а
, а 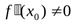 , то в этой точке функция имеет экстремум, причем максимум, если
, то в этой точке функция имеет экстремум, причем максимум, если 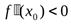 и минимум, если
и минимум, если 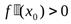 .
.
Пример 6.5. Найти точку экстремума функции  .
.
Найдем производные 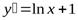 ;
; 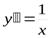 . Найдем критическую точку первого рода:
. Найдем критическую точку первого рода: 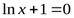 ,
, 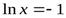 ,
,  - критическая точка. Вычислим
- критическая точка. Вычислим 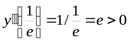 , значит
, значит  - абсцисса точки минимума. Минимум функции
- абсцисса точки минимума. Минимум функции 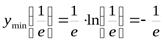 .
.
Если функция непрерывна в промежутке и имеет единственный экстремум, то он является наименьшим значением функции, если этот экстремум – минимум и наибольшим значением функции, если этот экстремум – максимум.
В прикладных экстремальных задачах нахождение наименьшего или наибольшего значения функции, как правило, сводится к нахождению минимума или максимума функции. В таких задачах больший практический интерес представляют не сами максимумы или минимумы, а те значения аргумента, при которых они достигаются. При решении прикладных задач главная трудность заключается в составлении функции, описывающей рассматриваемый процесс.
Пример 6.6. Дан квадратный лист жести со стороной а. Какого размера квадраты надо вырезать по его углам, чтобы, загнув края, получить коробку наибольшей вместимости.
Р  ешение. Обозначим через
ешение. Обозначим через 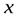 сторону квадрата, который надо вырезать. Тогда основанием коробки будет квадрат со стороной
сторону квадрата, который надо вырезать. Тогда основанием коробки будет квадрат со стороной 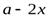 . Составим функцию объема коробки
. Составим функцию объема коробки 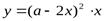 , где
, где 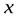 - высота коробки. Или
- высота коробки. Или  . Производная этой функции
. Производная этой функции 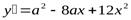 . Найдем критические значения
. Найдем критические значения 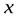 , решив уравнение
, решив уравнение 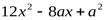 ,
,

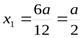 - не подходит по смыслу задачи;
- не подходит по смыслу задачи; 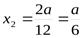
Проверим характер экстремума при помощи второй производной. Найдем 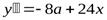 . Подставим
. Подставим  . Получим
. Получим 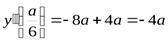 . Так как по смыслу задачи
. Так как по смыслу задачи 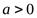 , то
, то 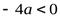 . А если
. А если 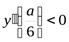 , то
, то 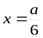 - сторона квадрата, при которой объем будет максимальным. Выше отмечалось, что если для непрерывной функции экстремум один и он является максимумом, то он и есть наибольшее значение функции.
- сторона квадрата, при которой объем будет максимальным. Выше отмечалось, что если для непрерывной функции экстремум один и он является максимумом, то он и есть наибольшее значение функции.
Дата: 2019-02-19, просмотров: 345.