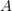 называется пределом функции
называется пределом функции 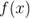 в точке
в точке  , если
, если 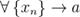 ,
, 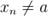 то есть
то есть 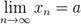 , соответствующая последовательность значений
, соответствующая последовательность значений 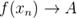 , то есть
, то есть 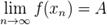 .
.
Геометрическая интерпретация
Основная идея метода заключается в следующем: задаётся начальное приближение вблизи предположительного корня, после чего строится касательная к исследуемой функции в точке приближения, для которой находится пересечение с осью абсцисс. Эта точка и берётся в качестве следующего приближения. И так далее, пока не будет достигнута необходимая точность.
Пусть  — определённая на отрезке
— определённая на отрезке 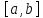 и дифференцируемая на нём вещественнозначная функция. Тогда формула итеративного исчисления приближений может быть выведена следующим образом:
и дифференцируемая на нём вещественнозначная функция. Тогда формула итеративного исчисления приближений может быть выведена следующим образом:
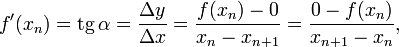
где 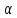 — угол наклона касательной в точкеxn.
— угол наклона касательной в точкеxn.
Следовательно искомое выражение для xn+1 имеет вид:
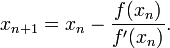
Итерационный процесс начинается с некоего начального приближения (чем ближе к нулю, тем лучше, но если предположения о нахождении решения отсутствуют, методом проб и ошибок можно сузить область возможных значений, применив теорему о промежуточных значениях).
Эквивалентность определений
Пусть число 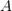 является пределом функции
является пределом функции 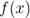 в точке
в точке  по Коши. Выберем произвольную подходящую последовательность
по Коши. Выберем произвольную подходящую последовательность 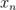 ,
, 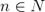 , то есть такую, для которой
, то есть такую, для которой  . Покажем, что
. Покажем, что 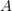 является пределом по Гейне.
является пределом по Гейне.
Зададим произвольное 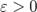 и укажем для него такое
и укажем для него такое 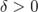 , что для всех
, что для всех  из условия
из условия 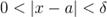 следует неравенство
следует неравенство 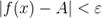 . В силу того, что
. В силу того, что 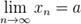 , для
, для 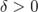 найдётся такой номер
найдётся такой номер 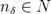 , что
, что 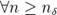 будет выполняться неравенство
будет выполняться неравенство 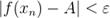 , то есть
, то есть 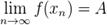 .
.
Докажем теперь обратное утверждение: предположим, что  по Гейне, и покажем, что число
по Гейне, и покажем, что число 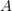 является пределом функции
является пределом функции 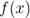 в точке
в точке  по Коши. Предположим, что это неверно, то есть: . В качестве
по Коши. Предположим, что это неверно, то есть: . В качестве 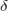 рассмотрим
рассмотрим 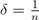 , а соответствующие значения
, а соответствующие значения 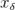 будем обозначать
будем обозначать 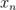 . Тогда при любом
. Тогда при любом 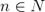 выполняются условия
выполняются условия 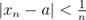 и
и 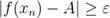 . Отсюда следует, что последовательность
. Отсюда следует, что последовательность  является подходящей, но число
является подходящей, но число 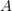 не является пределом функции
не является пределом функции 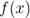 в точке
в точке  . Получили противоречие.
. Получили противоречие.
16) Односторонние пределы. Теорема о существовании предела функции в точке.
Под односторонним пределом числовой функции подразумевают «приближение» к предельной точке с одной стороны. Такие пределы называют соответственно левосторонним пределом (или пределом слева) (рис. 1) и правосторонним пределом (пределом справа) (рис. 2).
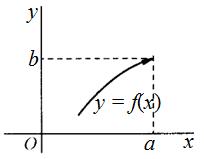
Рис.1 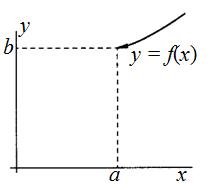 Рис.2
Рис.2
учебник: В.С. Шипачёв - высшая математика ( у нас есть ) -стр 77,теорема 4.2(сложна)
Теорема (теорема "о двух милиционерах") Пусть даны три функции f1(x),f2(x) и ϕ(x) , cвязанные условием 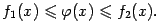 Пусть функции f1(x),f2(x) имеют общий предел L. Тогда функция ϕ(x) так же имеет предел .
Пусть функции f1(x),f2(x) имеют общий предел L. Тогда функция ϕ(x) так же имеет предел .
.Два милиционера f1(x),f2(x) и ϕ(x) пьяный движутся в участок 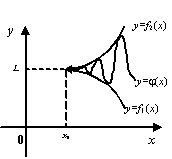
Дополнительно:
Ԑ > 0 - произвольное фиксированное число.
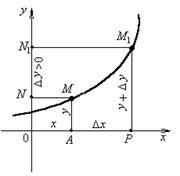
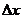 выражает ту величину, на которую изменяется аргумент при переходе от первого значения аргумента ко второму, и называется приращением аргумента.
выражает ту величину, на которую изменяется аргумент при переходе от первого значения аргумента ко второму, и называется приращением аргумента.
17)Свойства функций, имеющих конечный предел.
Т.2.1. Если функция в точке имеет предел, то он единственный.
Рассмотрим два свойства функции: о сохранении знака и об ограниченности.
Т.3.1 Если функция имеет конечный предел в некоторой точке, то существует такая 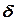 - окрестность этой точки, в которой функция будет принимать значения того же знака, что и предел:
- окрестность этой точки, в которой функция будет принимать значения того же знака, что и предел:
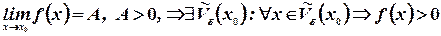 .
.
О.3.1 Функция 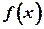 называется ограниченной на
называется ограниченной на 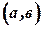 , если существует положительное число
, если существует положительное число 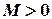 , что для всех значений аргумента из этого промежутка выполняется неравенство
, что для всех значений аргумента из этого промежутка выполняется неравенство 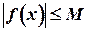 .
.
Т.3.2 Если функция имеет конечный предел в  , то существует некоторая
, то существует некоторая 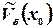 - окрестность в которой она ограничена (кроме самой
- окрестность в которой она ограничена (кроме самой  может
может
быть).
Т.3.3 Если функция  имеет конечный предел, в некоторой
имеет конечный предел, в некоторой 
отличный от нуля, то функция  ограничена.
ограничена.
18)Бесконечно малые и бесконечно большие функции. Теорема об их связи. Свойства бесконечно малых и бесконечно больших функций.
Функция y=f(x)называетсябесконечно малой(илибесконечно малой величиной) при  , если
, если 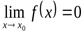 . Например,
. Например, 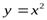 б.м. при х→0, т.к.f(x) →0, т.е.
б.м. при х→0, т.к.f(x) →0, т.е. 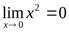 .
.
Аналогично определяется б.м.ф. при х→±∞, 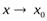 + и
+ и 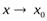 -.
-.
Дата: 2019-02-19, просмотров: 365.