Последовательность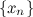 
называется ограниченной сверху, если существует такое число 
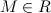, что для любого номера 
, 
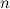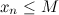
Последовательность 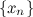называется ограниченной снизу, если существует такое число 
, что для любого номера , 
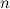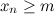
Последовательность 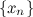называется ограниченной, если она ограниченная сверху и ограниченная снизу, то есть существует такое число 
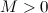, что для любого номера , 
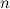Последовательность 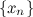называется неограниченной, если существует такое число 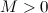, что существует такой номер 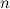, что 
Теорема. Числовое множество X ограничено тогда и только тогда, когда существует число C такое, что для всех элементов x из этого множества выполняется неравенство ≤ C.
Доказательство.► Пусть множество X ограничено. Положим C =max(m, M) - наибольшее из чисел m и M. Тогда, используя свойства модуля вещественных чисел, получим неравенства x ≤M≤M ≤C и x≥m≥ −m≥ −C, откуда следует, что ≤ C .
Обратно, если выполняется неравенство ≤ C , то −C ≤ x ≤ C . Это и есть требуемое, если положить M = C и m = −C .◄
Число M , ограничивающее множество X сверху, называется верхней границей множества. Если M - верхняя граница множества X , то любое число M′, которое больше M , тоже будет верхней границей этого множества. Таким образом, мы можем говорить о множестве верхних границ множества X. Обозначим множество верхних границ через . Тогда, ∀x ∈ X и ∀M ∈ будет выполнено неравенство x ≤M , следовательно, по аксиоме непрерывности существует число такое, что x ≤ ≤ M . Это число называется точной верхней границей числового множества X или верхней гранью этого множества или супремумом множества X и обозначается =sup X . Таким образом, мы доказали, что каждое непустое числовое множество, ограниченное сверху, всегда имеет точную верхнюю границу.
6)Два определения предела числовой последовательности. Примеры.
Функция f(x) называется функцией целочисленного аргумента, если множество значений x, для которых она определена, является множеством всех натуральных чисел1, 2, 3,… Примером функции целочисленного аргумента может служить сумма n первых чисел натурального ряда. В данном случае
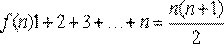
Числовой последовательностью называется бесконечное множество чисел
Пример 1.
Найти общий член последовательности 1, 4, 9, 16, 25, …
Р е ш е н и е : нетрудно видеть, что
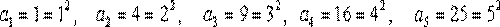и т.д.
Следовательно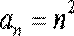 
Пример 2.
Найти общий член последовательности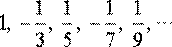 
Р е ш е н и е : не трудно видеть, что
, 
, 
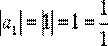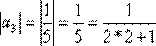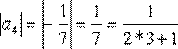и т.д.
Следовательно:
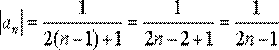
7)Свойства сходящихся последовательностей (единственность предела, ограниченность).
8) Теорема об арифметических операциях со сходящимися последовательностями.
Пусть последовательность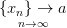 
, а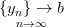 
. Тогда верны следующие утверждения:
Доказательство.
1. 
,
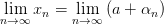
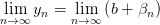где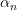 
и 
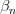— бесконечно малые последовательности.
2. 
, 
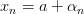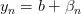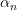, где и 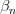— бесконечно малые последовательности.
(по свойству бесконечно малых последовательностей)
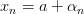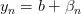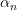3. , , где и 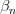— бесконечно малые последовательности.
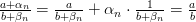
(по свойству бесконечно малых последовательностей)
9) Теоремы о предельном переходе в неравенствах.
Теорема. Если элементы сходящейся последовательности {xn}, начиная с некоторого номера, удовлетворяют неравенству xn ≥ b (xn ≤ b), то и предел a этой последовательности удовлетворяет неравенству a ≥ b (a ≤ b).
Доказательство. Пусть все элементы xn, по крайней мере начиная с некоторого номера, удовлетворяют неравенству xn ≥ b. Требуется доказать неравенство a ≥ b. Предположим, что a < b. Поскольку a - предел последовательности {xn}, то для положительного ε = b - a можно указать номер Nтакой, что при n ≥ N выполняется неравенство |xn - a| < b - a. Это неравенство эквивалентно следующим двум неравенствам: -(b - a) < xn - a < b -a. Используя правое из этих неравенств, получим xn < b, а это противоречит условию теоремы. Случай xn ≤ b рассматривается аналогично. Теорема доказана.
10Бесконечно большие и бесконечно малые последовательности. Теорема об их связи.
Определение 3.5.Последовательность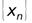 
называется бесконечно большой, если для любого сколь угодно большого числа 
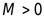найдется такой номер 
, что для всех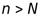 
справедливо неравенство 
.
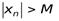Тот факт, что последовательность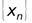 
бесконечно большая, символически записывается следующим образом:
Рассмотрим последовательности
;
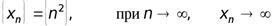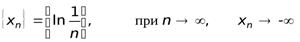
Таким образом, представленные последовательности будут бесконечно большими. Такие последовательности называются расходящимися.
Определение 3.6. Последовательность называется бесконечно малой или нуль - последовательностью, если выполняется условие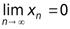 
.
Теорема 3.1.Алгебраическая сумма двух бесконечно малых есть величина бесконечно малая.
Теорема 3.2.Произведение ограниченной последовательности и бесконечно малой есть последовательность бесконечно малая.
Непосредственно связь между бесконечно малыми и бесконечно большими устанавливают следующие утверждения. Утверждение 3.1.Величина, обратная к бесконечно большой, есть бесконечно малая, т.е.
если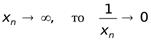 
.
Утверждение 3.2. Величина, обратная к бесконечно малой, есть бесконечно большая, т.е. если 
.
Практическое вычисление пределов числовых последовательностей основывается на следующих теоремах.
Теорема 3.3Последовательность может иметь не более одного предела.
Теорема 3.4.Алгебраическая сумма двух сходящихся последовательностей есть последовательность сходящаяся, и ее предел равен соответствующей сумме пределов последовательностей.
В соответствии с теоремой имеем
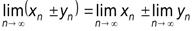
Теорема 3.5.Произведение двух сходящихся последовательностей есть последовательность сходящаяся, и ее предел равен произведению пределов заданных последовательностей.
В соответствии с теоремой имеем
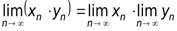
Теорема 3.6.Если последовательност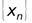и и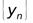 
сходящиеся, т.е. 
, 
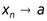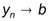и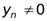 
для всех 
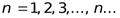,а также 
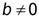, то последовательность 
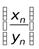также будет сходящейся и ее предел равен частному пределов последовательностей , 
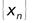и 
т.е.
.
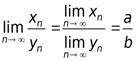11)Теоремы о произведении ограниченной последовательности на бесконечно малую и о связи членов последовательности со своим пределом.
Последовательность 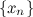называетсяограниченной сверху, если существует такое число 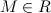, что для любого номера ,
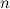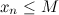
Последовательность 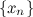называетсяограниченной снизу, если существует такое число , что для любого номера ,
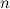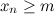
Последовательность 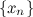называетсяограниченной, если она ограниченная сверху и ограниченная снизу, то есть существует такое число 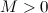, что для любого номера ,
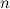Последовательность 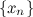называетсянеограниченной, если существует такое число 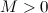, что существует такой номер 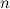, что
Теорема об ограниченности сходящейся последовательности
Если последовательность имеет конечный предел, то последовательность ограничена.
Определение. Числовая последовательность {xn} ограничена, если существует такое конечное число К, что для всех n выполнено
d (xn, a ) < K.
Доказательство. Пусть
Тогда
N: n > N: d (xn, a) < 1.
Внутри окрестности радиуса R = 1 бесконечное число точек, а вне этой окрестности конечное число точек, допустим, что это точки x1, x2, … xN. Выберем число, тогда уже для всех n будет выполнено
d (xn, a ) < K.
12) Признаки сходимости монотонных последовательностей (три теоремы Вейерштрасса).
в тетради
13) По признаку Вейерштрасса доказать, что последовательность имеет предел.
в тетради
14) δ-окрестность конечной и бесконечных точек. Предельные точки множества.
1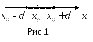 
). 
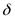-окрестность конечной точки 
обозначим 
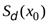и определим как множество действительных чисел 
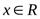таких, что 
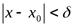(рис.1):
2 
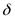). -окрестность бесконечностиобозначим 
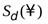и определим как множество действительных чисел 
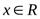таких, что 
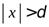(рис.2). Итак,
.
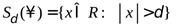
3
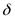). -окрестность плюс бесконечностиопределим (рис.3) как
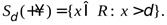
4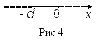 
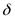). -окрестность минус бесконечности определим (рис 4) как
.
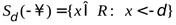5 ). Введём понятиевыколотой окрестност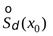и 
точки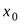 
, которая получается из окрестности 
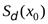удалением точки :
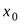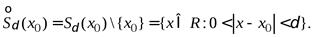
Пусть . Число называется предельной точкой множества X, если
Из определения следует, что любая окрестность точки x0 содержит точку из множества X, отличную от x0. Сама точка x0 может принадлежать, а может и не принадлежать множеству X.
Значение +∞ есть предельная точка множества X, если
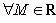
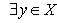
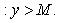
Значение -∞ предельная точка множества X, еслиесли
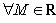
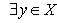
Точка , не являющаяся предельной точкой множества X, называется изолированнойточкой множества X, т. т. е.
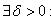
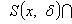
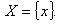
Число называется предельной точкой множества , если из этого множества можно выделить последовательность (xn) различных точек, сходящуюся к x0. (Данное определение и определение, указанное в самом начале эквивалентны)
15) Определения предела функции по Гейне и по Коши. Геометрическая интерпретация. Эквива-лентность определений предела функции по Гейне и по Коши .
Определение 1.1. (определение по Коши )
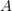— предел функции 
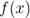в точке 
(и пишут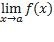 
=A), если: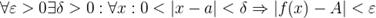 
В определении допускается, что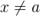 
, то есть может не принадлежать
Дата: 2019-02-19, просмотров: 243.
