Для заданной функции
f (- x )= 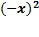 =
= 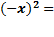 f ( x )
f ( x )
Значит, эта функция четная.
Ответ Функция четная.
Функция f(x)= sin x является периодической, так как
f( x+2π)=sin (x+2π)=sin x
Период этой функции T=2π
Основные элементарные функции+тетрадь
1. Степенная функция
 ,
,  .
.
2. Показательная функция
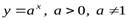 .
.
3. Логарифмическая функция
 .
.
4. Тригонометрические функции
 .
.
5. Обратные тригонометрические функции
 .
.

Пусть функция y=f(x) определена на множестве D, а E — множество её значений. Обратная функция по отношению к функции y=f(x) — это функция x=g(y), которая определена на множестве E и каждому y ∈ E ставит в соответствие такое значение x ∈ D, что f(x)=y.
Таким образом, область определения функции y=f(x) является областью значений обратной к ней функции, а область значений y=f(x) — областью определения обратной функции.
Чтобы найти функцию, обратную данной функции y=f(x), надо:
1) В формулу функции вместо y подставить x, вместо x — y:
x=f(y).
2) Из полученного равенства выразить y через x:
y=g(x).
Пример.
Найти функцию, обратную функции y=2x-6.
1) x=2y-6
2) -2y=-x-6
y=0,5x+3.
Функции y=2x-6 и y=0,5x+3 являются взаимно обратными.
Под неявным заданием функции понимают задание функции в виде уравнения F(x;y)=0, не разрешенного относительно у.
Всякую явно заданную функцию у=ƒ (х) можно записать как неявно заданную уравнением ƒ(х)-у=0, но не наоборот.
Не всегда легко, а иногда и невозможно разрешить уравнение относительно у (например, у+2х+cosy-1=0 или 2у-х+у=0).
Если неявная функция задана уравнением F(x; у)=0, то для нахождения производной от у по х нет необходимости разрешать уравнение относительно у: достаточно продифференцировать это уравнение по x, рассматривая при этом у как функцию х, и полученное затем уравнение разрешить относительно у'.
Производная неявной функции выражается через аргумент х и функцию у.
Связь между аргументом и функцией может быть записана через дополнительную переменную, называемую параметром, то есть в виде системы, в которой прописывается зависимость аргумента от параметра и зависимость функции от того же параметра:
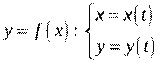 , где
, где 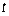 – это параметр,
– это параметр, 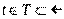 .
.
В этом случае функция называетсяфункцией, заданной параметрически.
График функции
Графиком функции y = f(x) называется множество всех точек, у которых абсциссы принадлежат области определения функции, а ординаты равны соответствующим значениям функции.
Другими словами, график функции y = f (х) - это множество всех точек плоскости, координаты х, у которых удовлетворяют соотношению y = f(x).
3) Декартовы и полярные координаты на плоскости. Примеры кривых в полярных координатах.
Декартова система координат на плоскости определяется некоторой ее точкой O и базисом из двух векторов, параллельных плоскости. Точка Oназывается началом координат. Прямые, проведенные через начало координат в направлении базисных векторов, называются осями координат. Они лежат в плоскости и называются осями абсцисс и ординат. Каждая ось координат является числовой осью с началом в точке O, положительным направлением, совпадающим с направлением соответствующего базисного вектора, и единицей длины, равной длине этого вектора.
Координатами точки M называются координаты вектора OM (радиус–вектора) (см. рис. 1).

Если базис ортонормированный, то связанная с ним декартова система координат называется прямоугольной.
На плоскости часто употребляется также полярная система координат (рис. 2).
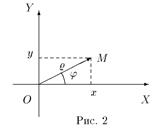
Она определяется точкой O, называемой полюсом, и лучом, исходящим из полюса, называемым полярной осью. Полярными координатами ρ и j точкиM называются расстояние ρ от полюса до точки M ( ρ = |OM|) и угол j между полярной осью и вектором OM (рис. 2). Угол j называется полярным углом, измеряется в радианах и отсчитывается от полярной оси против часовой стрелки. Полярные координаты точки O: ρ = 0, угол j не определен. У остальных точек ρ > 0 и угол j определен с точностью до 2π. Обычно полагают 0 ≤ j < 2 π или − π < j ≤ π.
Если полюс совпадает с началом прямоугольной декартовой системы координат, а полярная ось — с положительной частью оси абсцисс, то декартовы координаты x и y точки M выражаются через ее полярные координаты ρ и j формулами
x = ρcosj y = ρsinj .
4)Линейная интерполяция. Интерполяционный многочлен Лагранжа.
Лине́йная интерполя́ция — интерполяция алгебраическим двучленом P1(x) = ax + b функции f, заданной в двух точках x0 и x1 отрезка [a, b]. В случае, если заданы значения в нескольких точках, функция заменяется кусочно-линейной функцией.
Простейшим и часто используемым видом локальной интерполяции является линейная интерполяция. Она состоит в том, что заданные точки (xi,yi) при (i = 0. 1, ..., n) соединяются прямолинейными отрезками, и функция f(x) приближается ломаной с вершинами в данных точках.
Уравнения каждого отрезка ломаной в общем случае разные. Поскольку имеется n интервалов (xi-1,xi), то для каждого из них в качестве уравнения интерполяционного многочлена используется уравнение прямой, проходящей через две точки. В частности, для i-го интервала можно написать уравнение прямой, проходящей через точки(xi-1,yi-1) и (xi,yi), в виде
 =
= 
5 )Определение числовой последовательности. Определение монотонной, ограниченной, неогра-ниченной последовательностей. Определение последовательности, ограниченной сверху, ограниченной снизу. Теорема о свойстве верхней грани.
Числовая последовательность — это последовательность элементов числового пространства.
Последовательность 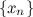 называется монотонно возрастающей, если для любого
называется монотонно возрастающей, если для любого 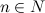 ,
, 
пример
Последовательность 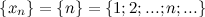 является возрастающей, так как для любого
является возрастающей, так как для любого 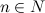 ,
, 
Пример 1.
Найти общий член последовательности 1, 4, 9, 16, 25, …
Р е ш е н и е : нетрудно видеть, что
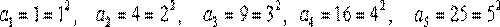 и т.д.
и т.д.
Следовательно 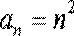
Пример 2.
Найти общий член последовательности 
Р е ш е н и е : не трудно видеть, что
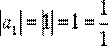 ,
, 
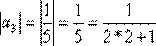 ,
, 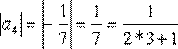 и т.д.
и т.д.
Следовательно:
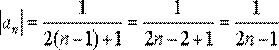
7)Свойства сходящихся последовательностей (единственность предела, ограниченность).

8) Теорема об арифметических операциях со сходящимися последовательностями.
Пусть последовательность 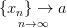 , а
, а 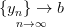 . Тогда верны следующие утверждения:
. Тогда верны следующие утверждения:
 Доказательство.
Доказательство.
1. 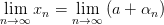
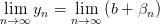 ,
,
где 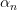 и
и  — бесконечно малые последовательности.
— бесконечно малые последовательности.
2.  ,
,  , где
, где 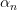 и
и  — бесконечно малые последовательности.
— бесконечно малые последовательности.
(по свойству бесконечно малых последовательностей)
3.  ,
,  , где
, где 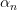 и
и  — бесконечно малые последовательности.
— бесконечно малые последовательности.

(по свойству бесконечно малых последовательностей)
9) Теоремы о предельном переходе в неравенствах.
Теорема. Если элементы сходящейся последовательности {xn}, начиная с некоторого номера, удовлетворяют неравенству xn ≥ b (xn ≤ b), то и предел a этой последовательности удовлетворяет неравенству a ≥ b (a ≤ b).
Доказательство. Пусть все элементы xn, по крайней мере начиная с некоторого номера, удовлетворяют неравенству xn ≥ b. Требуется доказать неравенство a ≥ b. Предположим, что a < b. Поскольку a - предел последовательности {xn}, то для положительного ε = b - a можно указать номер Nтакой, что при n ≥ N выполняется неравенство |xn - a| < b - a. Это неравенство эквивалентно следующим двум неравенствам: -(b - a) < xn - a < b -a. Используя правое из этих неравенств, получим xn < b, а это противоречит условию теоремы. Случай xn ≤ b рассматривается аналогично. Теорема доказана.
10Бесконечно большие и бесконечно малые последовательности. Теорема об их связи.
Определение 3.5.Последовательность 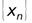 называется бесконечно большой, если для любого сколь угодно большого числа
называется бесконечно большой, если для любого сколь угодно большого числа 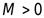 найдется такой номер
найдется такой номер  , что для всех
, что для всех  справедливо неравенство
справедливо неравенство 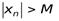 .
.
Тот факт, что последовательность  бесконечно большая, символически записывается следующим образом:
бесконечно большая, символически записывается следующим образом:

Рассмотрим последовательности
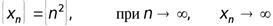 ;
;
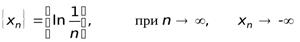
Таким образом, представленные последовательности будут бесконечно большими. Такие последовательности называются расходящимися.
Определение 3.6. Последовательность называется бесконечно малой или нуль - последовательностью, если выполняется условие  .
.
Теорема 3.1.Алгебраическая сумма двух бесконечно малых есть величина бесконечно малая.
Теорема 3.2.Произведение ограниченной последовательности и бесконечно малой есть последовательность бесконечно малая.
Непосредственно связь между бесконечно малыми и бесконечно большими устанавливают следующие утверждения. Утверждение 3.1.Величина, обратная к бесконечно большой, есть бесконечно малая, т.е.
если 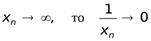 .
.
Утверждение 3.2. Величина, обратная к бесконечно малой, есть бесконечно большая, т.е. если  .
.
Практическое вычисление пределов числовых последовательностей основывается на следующих теоремах.
Теорема 3.3Последовательность может иметь не более одного предела.
Теорема 3.4.Алгебраическая сумма двух сходящихся последовательностей есть последовательность сходящаяся, и ее предел равен соответствующей сумме пределов последовательностей.
В соответствии с теоремой имеем

Теорема 3.5.Произведение двух сходящихся последовательностей есть последовательность сходящаяся, и ее предел равен произведению пределов заданных последовательностей.
В соответствии с теоремой имеем
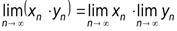
Теорема 3.6.Если последовательности  и
и  сходящиеся, т.е.
сходящиеся, т.е. 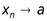 ,
,  и
и 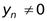 для всех
для всех 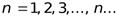 ,а также
,а также 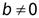 , то последовательность
, то последовательность 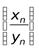 также будет сходящейся и ее предел равен частному пределов последовательностей ,
также будет сходящейся и ее предел равен частному пределов последовательностей , 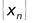 и
и  т.е.
т.е.
 .
.
11)Теоремы о произведении ограниченной последовательности на бесконечно малую и о связи членов последовательности со своим пределом.
Последовательность 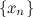 называетсяограниченной сверху, если существует такое число
называетсяограниченной сверху, если существует такое число 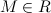 , что для любого номера
, что для любого номера 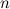 ,
, 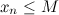
Последовательность 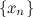 называетсяограниченной снизу, если существует такое число
называетсяограниченной снизу, если существует такое число  , что для любого номера
, что для любого номера 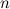 ,
, 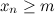
Последовательность 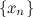 называетсяограниченной, если она ограниченная сверху и ограниченная снизу, то есть существует такое число
называетсяограниченной, если она ограниченная сверху и ограниченная снизу, то есть существует такое число 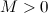 , что для любого номера
, что для любого номера 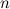 ,
, 
Последовательность 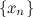 называетсянеограниченной, если существует такое число
называетсянеограниченной, если существует такое число 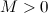 , что существует такой номер
, что существует такой номер 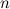 , что
, что 
Теорема об ограниченности сходящейся последовательности
Если последовательность имеет конечный предел, то последовательность ограничена.
Определение. Числовая последовательность {xn} ограничена, если существует такое конечное число К, что для всех n выполнено
d (xn, a ) < K.
Доказательство. Пусть
Тогда
N: n > N: d (xn, a) < 1.
Внутри окрестности радиуса R = 1 бесконечное число точек, а вне этой окрестности конечное число точек, допустим, что это точки x1, x2, … xN. Выберем число, тогда уже для всех n будет выполнено
d (xn, a ) < K.
12) Признаки сходимости монотонных последовательностей (три теоремы Вейерштрасса).
в тетради
13) По признаку Вейерштрасса доказать, что последовательность имеет предел.
в тетради
14) δ-окрестность конечной и бесконечных точек. Предельные точки множества.
1 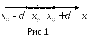 ).
).  -окрестность конечной точки
-окрестность конечной точки  обозначим
обозначим 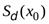 и определим как множество действительных чисел
и определим как множество действительных чисел  таких, что
таких, что 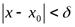 (рис.1):
(рис.1):

2  ).
).  -окрестность бесконечностиобозначим
-окрестность бесконечностиобозначим 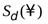 и определим как множество действительных чисел
и определим как множество действительных чисел 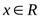 таких, что
таких, что 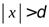 (рис.2). Итак,
(рис.2). Итак,

 .
.
3

 ).
).  -окрестность плюс бесконечностиопределим (рис.3) как
-окрестность плюс бесконечностиопределим (рис.3) как
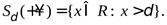
4  ).
).  -окрестность минус бесконечности определим (рис 4) как
-окрестность минус бесконечности определим (рис 4) как
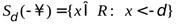 .
.
5  ). Введём понятиевыколотой окрестности
). Введём понятиевыколотой окрестности 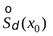 точки
точки 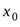 , которая получается из окрестности
, которая получается из окрестности 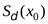 удалением точки
удалением точки 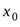 :
:
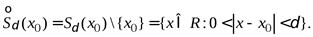
Пусть . Число называется предельной точкой множества X, если
Из определения следует, что любая окрестность точки x0 содержит точку из множества X, отличную от x0. Сама точка x0 может принадлежать, а может и не принадлежать множеству X.
Значение +∞ есть предельная точка множества X, если
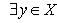
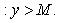
Значение -∞ предельная точка множества X, еслиесли

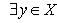

Точка , не являющаяся предельной точкой множества X, называется изолированнойточкой множества X, т. т. е.
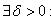
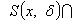
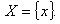
Число называется предельной точкой множества , если из этого множества можно выделить последовательность (xn) различных точек, сходящуюся к x0. (Данное определение и определение, указанное в самом начале эквивалентны)
15) Определения предела функции по Гейне и по Коши. Геометрическая интерпретация. Эквива-лентность определений предела функции по Гейне и по Коши .
Определение 1.1. (определение по Коши )
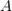 — предел функции
— предел функции 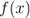 в точке
в точке  (и пишут
(и пишут 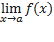 =A), если:
=A), если: 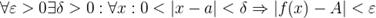
В определении допускается, что 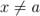 , то есть
, то есть  может не принадлежать
может не принадлежать
Эквивалентность определений
Пусть число 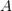 является пределом функции
является пределом функции 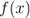 в точке
в точке  по Коши. Выберем произвольную подходящую последовательность
по Коши. Выберем произвольную подходящую последовательность 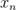 ,
, 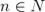 , то есть такую, для которой
, то есть такую, для которой  . Покажем, что
. Покажем, что 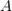 является пределом по Гейне.
является пределом по Гейне.
Зададим произвольное 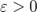 и укажем для него такое
и укажем для него такое 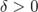 , что для всех
, что для всех  из условия
из условия 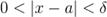 следует неравенство
следует неравенство 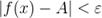 . В силу того, что
. В силу того, что  , для
, для 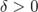 найдётся такой номер
найдётся такой номер 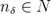 , что
, что 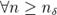 будет выполняться неравенство
будет выполняться неравенство 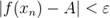 , то есть
, то есть 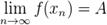 .
.
Докажем теперь обратное утверждение: предположим, что  по Гейне, и покажем, что число
по Гейне, и покажем, что число 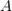 является пределом функции
является пределом функции 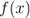 в точке
в точке  по Коши. Предположим, что это неверно, то есть: . В качестве
по Коши. Предположим, что это неверно, то есть: . В качестве 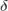 рассмотрим
рассмотрим 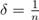 , а соответствующие значения
, а соответствующие значения  будем обозначать
будем обозначать 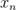 . Тогда при любом
. Тогда при любом 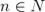 выполняются условия
выполняются условия 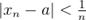 и
и 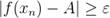 . Отсюда следует, что последовательность
. Отсюда следует, что последовательность  является подходящей, но число
является подходящей, но число 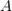 не является пределом функции
не является пределом функции 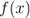 в точке
в точке  . Получили противоречие.
. Получили противоречие.
16) Односторонние пределы. Теорема о существовании предела функции в точке.
Под односторонним пределом числовой функции подразумевают «приближение» к предельной точке с одной стороны. Такие пределы называют соответственно левосторонним пределом (или пределом слева) (рис. 1) и правосторонним пределом (пределом справа) (рис. 2).

Рис.1 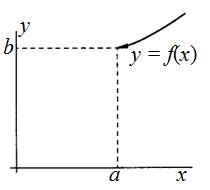 Рис.2
Рис.2
учебник: В.С. Шипачёв - высшая математика ( у нас есть ) -стр 77,теорема 4.2(сложна)
Теорема (теорема "о двух милиционерах") Пусть даны три функции f1(x),f2(x) и ϕ(x) , cвязанные условием  Пусть функции f1(x),f2(x) имеют общий предел L. Тогда функция ϕ(x) так же имеет предел .
Пусть функции f1(x),f2(x) имеют общий предел L. Тогда функция ϕ(x) так же имеет предел .
.Два милиционера f1(x),f2(x) и ϕ(x) пьяный движутся в участок 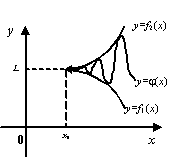
Дополнительно:
Ԑ > 0 - произвольное фиксированное число.
 выражает ту величину, на которую изменяется аргумент при переходе от первого значения аргумента ко второму, и называется приращением аргумента.
выражает ту величину, на которую изменяется аргумент при переходе от первого значения аргумента ко второму, и называется приращением аргумента.
17)Свойства функций, имеющих конечный предел.
Т.2.1. Если функция в точке имеет предел, то он единственный.
Рассмотрим два свойства функции: о сохранении знака и об ограниченности.
Т.3.1 Если функция имеет конечный предел в некоторой точке, то существует такая  - окрестность этой точки, в которой функция будет принимать значения того же знака, что и предел:
- окрестность этой точки, в которой функция будет принимать значения того же знака, что и предел:
 .
.
О.3.1 Функция 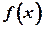 называется ограниченной на
называется ограниченной на 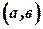 , если существует положительное число
, если существует положительное число 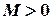 , что для всех значений аргумента из этого промежутка выполняется неравенство
, что для всех значений аргумента из этого промежутка выполняется неравенство 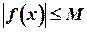 .
.
Т.3.2 Если функция имеет конечный предел в  , то существует некоторая
, то существует некоторая 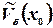 - окрестность в которой она ограничена (кроме самой
- окрестность в которой она ограничена (кроме самой  может
может
быть).
Т.3.3 Если функция  имеет конечный предел, в некоторой
имеет конечный предел, в некоторой 
отличный от нуля, то функция  ограничена.
ограничена.
18)Бесконечно малые и бесконечно большие функции. Теорема об их связи. Свойства бесконечно малых и бесконечно больших функций.
Функция y=f(x)называетсябесконечно малой(илибесконечно малой величиной) при  , если
, если 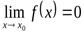 . Например,
. Например, 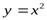 б.м. при х→0, т.к.f(x) →0, т.е.
б.м. при х→0, т.к.f(x) →0, т.е.  .
.
Аналогично определяется б.м.ф. при х→±∞, 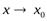 + и
+ и 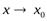 -.
-.
Доказательство
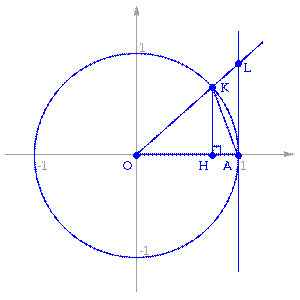
Рассмотрим односторонние пределы 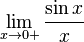 и
и 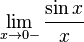 и докажем, что они равны 1.
и докажем, что они равны 1.
Пусть  . Отложим этот угол на единичной окружности (
. Отложим этот угол на единичной окружности (  ).
).
Точка K— точка пересечения луча с окружностью, а точкаL— с касательной к единичной окружности в точке  . ТочкаH— проекция точкиKна осьOX.
. ТочкаH— проекция точкиKна осьOX.
Очевидно, что:
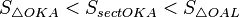 (1)
(1)
(где 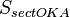 — площадь сектора
— площадь сектора  )
)
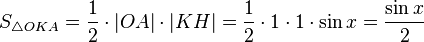
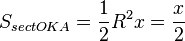
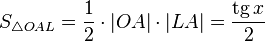
(из 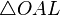 :
: 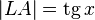 )
)
Подставляя в (1), получим:

Так как при  :
:
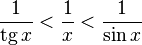
Умножаем на 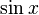 :
:
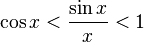
Перейдём к пределу:



Найдём левый односторонний предел:
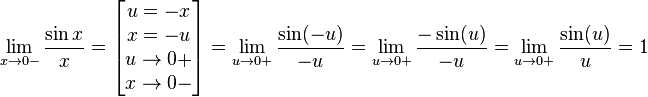
Правый и левый односторонний пределы существуют и равны 1, а значит и сам предел равен 1.
20) Второй замечательный предел :

Доказательство второго замечательного предела:
Доказательство для натуральных значений x [показать]
 Зная, что второй замечательный предел верен для натуральных значений x, докажем второй замечательный предел для вещественных x, то есть докажем, что
Зная, что второй замечательный предел верен для натуральных значений x, докажем второй замечательный предел для вещественных x, то есть докажем, что 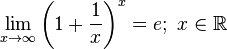 . Рассмотрим два случая:
. Рассмотрим два случая:
1. Пусть  . Каждое значение x заключено между двумя положительными целыми числами:
. Каждое значение x заключено между двумя положительными целыми числами: 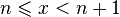 , где
, где 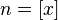 — это целая часть x.
— это целая часть x.
Отсюда следует:  , поэтому
, поэтому
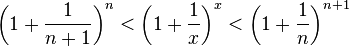 .
.
Если  , то
, то 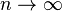 . Поэтому, согласно пределу
. Поэтому, согласно пределу  , имеем:
, имеем:
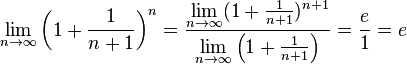
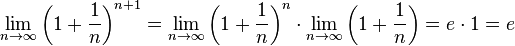 .
.
По признаку (о пределе промежуточной функции) существования пределов  .
.
2. Пусть  . Сделаем подстановку
. Сделаем подстановку 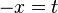 , тогда
, тогда

 .
.
Из двух этих случаев вытекает, что 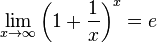 для вещественного x.
для вещественного x.
21) Сравнение бесконечно малых функций, пример


22) Свойства эквивалентных бесконечно малых.
Как известно, сумма, разность и произведение двух б.м.ф. есть функция бесконечно малая. Отношение же двух б.м.ф. может вести себя различным образом: быть конечным числом, быть бесконечно большой, бесконечно малой функцией или вообще не стремиться ни к какому пределу.
Две б.м.ф. сравниваются между собой с помощью их отношения.
Пусть 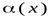 и
и  есть б.м.ф. при
есть б.м.ф. при 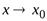 , т.е.
, т.е. 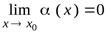 и
и 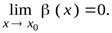
1. Если 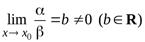 , то
, то 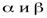 называютсябесконечно малыми одного порядка.
называютсябесконечно малыми одного порядка.
2. Если  , то
, то 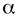 называетсябесконечно малой более высокого порядка, чем β.
называетсябесконечно малой более высокого порядка, чем β.
3. Если  , то
, то 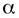 называетсябесконечно малой более низкого порядка, чем β.
называетсябесконечно малой более низкого порядка, чем β.
4. Если 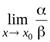 не существует, то
не существует, то 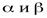 называютсянесравнимыми бесконечно малыми.
называютсянесравнимыми бесконечно малыми.
Пример Сравнить порядок функций  при
при 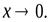
Решение. При  это б.м.ф. одного порядка, так как
это б.м.ф. одного порядка, так как

Говорят, что б.м.ф. 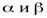 одного порядка стремятся к нулю с примерно одинаковой скоростью.
одного порядка стремятся к нулю с примерно одинаковой скоростью.
Пример Являются ли функции  б.м.ф. одного порядка при
б.м.ф. одного порядка при 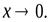
Решение. При 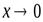 функция
функция 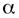 есть б.м.ф. более высокого порядка, чем β, так как
есть б.м.ф. более высокого порядка, чем β, так как 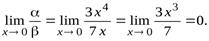 В этом случае б.м.ф.
В этом случае б.м.ф. 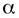 стремится к нулю быстрее, чем β.
стремится к нулю быстрее, чем β.
Пример Сравнить порядок функций 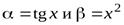 при
при 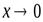 .
.
Решение. Так как  то
то 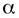 есть б.м.ф. более низкого порядка, чем β.
есть б.м.ф. более низкого порядка, чем β.
Пример Можно ли сравнить функции 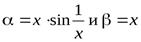 при
при 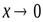 ?
?
23)Определения функции, непрерывной в точке. Их эквивалентность. Примеры.
Функция f(x) называется непрерывной в точке x0, если она определена на некоторой окрестности U(x0) этой точки, и если предел при x стремящемся к x0 существует и равен значению функции в x0: 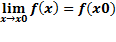 .
.
Здесь подразумевается, что x0 – это конечная точка. Значение функции в ней может быть только конечным числом.
Если привлечь сюда определение конечного предела функции в конечной точке, то можно дать развернутую формулировку определения непрерывности функции. Поскольку имеется два равносильных определения предела функции (по Коши и по Гейне), то можно дать, как минимум, еще два эквивалентных определения непрерывности.
Соответствие 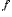 между элементами множеств
между элементами множеств 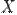 и
и 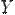 называетсяфункцией, еслилюбомуэлементу
называетсяфункцией, еслилюбомуэлементу  поставлен в соответствиеединственныйэлемент
поставлен в соответствиеединственныйэлемент  (это записывается следующим образом:
(это записывается следующим образом: 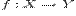 или
или  ).
).
Определение предела функции по Гейне.Пусть в каждой точке интервала 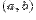 , кроме, быть может, точки
, кроме, быть может, точки 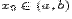 , определена функция
, определена функция 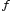 Число
Число 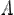 называетсяпределомфункции
называетсяпределомфункции 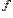 при стремлении
при стремлении 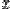 к
к 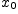 , если для любой последовательности
, если для любой последовательности 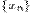 такой, что
такой, что  последовательность
последовательность 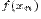 значений функции
значений функции 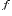 сходится к
сходится к 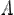 при
при  .В этом случае пишут
.В этом случае пишут 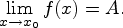
Пример. Пусть 
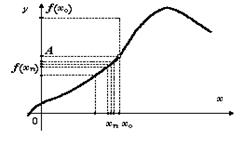
Предел функции 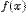 при
при 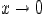 не существует, так как для
не существует, так как для  значения функции
значения функции 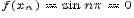 , а для
, а для 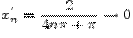 ,
,
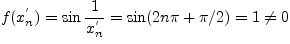 .
.
Пример.Пусть  Тогда
Тогда 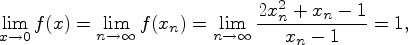 так как
так как 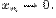
Определение предела функции по Коши.Пусть в каждой точке интервала 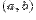 , кроме, быть может, точки
, кроме, быть может, точки 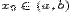 , определена функция
, определена функция 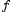 . Число
. Число 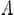 называетсяпределомфункции
называетсяпределомфункции 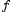 при стремлении
при стремлении 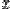 к
к 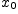 , если для любого
, если для любого 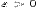 существует
существует 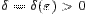 такое, что для всех
такое, что для всех 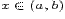 , удовлетворяющих условию
, удовлетворяющих условию  , выполняется неравенство
, выполняется неравенство 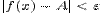 . Или, на формальном языке,
. Или, на формальном языке, 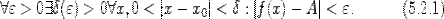

24)Локальные свойства функций, непрерывных в точке.
Локальными называют такие свойства функций, которые определяются поведением функции в сколь угодно малой окрестности точки области определения.
Теорема (формулировка)
Пусть f:E→R — функция, непрерывная в точке x0∈R тогда справедливы следующие утверждения:
· Функция f ограничена в некоторой окрестности UE(x0).
· Если f(x0)≠0, то в некоторой окрестности UE(x0) точки x0 функция f(x)>0
( или f(x)<0 ) вместе с f(x0).
· Если функция g:UE(x0) →R также непрерывна в точке x0, то следующие функции непрерывны в точке x0:
§ f+g
§ f⋅g
§ f/g
Если функция g:Y →R непрерывна в точке y0∈Y, а функция f такова, что f:E →R, f(x0)=y0, f(E)∈Y и f непрерывна в точке x0, то композиция g∘f непрерывна в точке x0.
Пример 1
Алгебраический многочлен Pn(x)=a0xn+a1xn−1+…+an является непрерывной функцией для x∈R. Это следует из теоремы 1 и непрерывности функции y=x и y=k.
Пример 2
Рациональная функция R(x)=Pn(x)Qm(x) непрерывна всюду, кроме точек, в которых Qm(x)=0.
25)Определение функции, непрерывной на отрезке. Непрерывность элементарных функций и до-казательство для y=sin(x)
Функция, непрерывная во всех точках некоторой области, называется непрерывной в этой области.
Функция  называется непрерывной справа в точке
называется непрерывной справа в точке  , если
, если  .
.
Функция  называется непрерывной слева в точке
называется непрерывной слева в точке  , если
, если 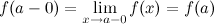 .
.
Функция 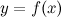 называется непрерывной в интервале
называется непрерывной в интервале 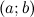 , если она непрерывна в каждой точке этого интервала.
, если она непрерывна в каждой точке этого интервала.
Функция 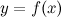 называется непрерывной на отрезке
называется непрерывной на отрезке 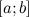 , если она является непрерывной в интервале
, если она является непрерывной в интервале 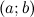 , непрерывной справа в точке
, непрерывной справа в точке  , то есть
, то есть 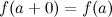 и непрерывной слева в точке
и непрерывной слева в точке 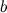 , то есть
, то есть 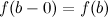 .
.
Функция y = sin x
При вычислении предела 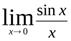 было установлено, что если
было установлено, что если 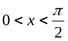 , то
, то 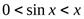 . Ввиду нечетности функцийy=x и y= sin x, при
. Ввиду нечетности функцийy=x и y= sin x, при 
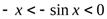 . Из этого сразу следует, что при
. Из этого сразу следует, что при 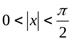 выполняется неравенство
выполняется неравенство  . Пустьx0 произвольная точка. Докажем, что
. Пустьx0 произвольная точка. Докажем, что 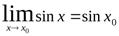 . Это равносильно тому, что
. Это равносильно тому, что  . В свою очередь, это равносильно тому, что
. В свою очередь, это равносильно тому, что 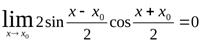 . Так как, по доказанному выше,
. Так как, по доказанному выше, 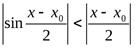 ,
, 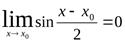 . Кроме того, функция 2cos
. Кроме того, функция 2cos 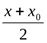 , очевидно, ограниченная. По свойствам бесконечно малых, получаем требуемое
, очевидно, ограниченная. По свойствам бесконечно малых, получаем требуемое
26Глобальные свойства непрерывных функций (теоремы Больцано-Коши и Вейершрасса).)
Односторонние производные
Введем понятия левой и правой производных функции  по аналогии с понятием левого и правого предела.
по аналогии с понятием левого и правого предела.
ОПРЕДЕЛЕНИЕ. Правой производной функции  в точке
в точке  называется
называется  при условии, что этот предел существует.
при условии, что этот предел существует.
То, что  означает, что
означает, что  , то есть при вычислении правой производной
, то есть при вычислении правой производной 
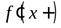 к точке
к точке  приближаются справа.
приближаются справа.
ОПРЕДЕЛЕНИЕ. Левой производной функции 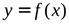 в точке
в точке 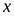 называется
называется  при условии, что этот предел существует.
при условии, что этот предел существует.
При вычислении левой производной  полагается
полагается  .
.
Имеют место утверждения:
1. если функция имеет в точке  производную
производную 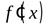 , то она имеет в этой точке как левую, так и правую производные, причем
, то она имеет в этой точке как левую, так и правую производные, причем 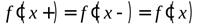
2. если функция имеет в точке 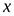 как правую, так и левую производные, причем эти производные равны между собой, то в точке
как правую, так и левую производные, причем эти производные равны между собой, то в точке 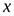 существует производная, причем
существует производная, причем 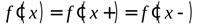 .
.
3. если 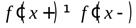 , то в точке
, то в точке  функция не имеет производной.
функция не имеет производной.
ПРИМЕР. Рассмотрим функцию  .
.
Вычислим односторонние производные (правую и левую) в точке 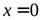 .
.
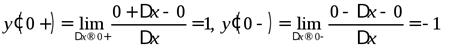 . Односторонние производные неравны, значит,
. Односторонние производные неравны, значит,  не существует. В других точках эта функция производную имеет.
не существует. В других точках эта функция производную имеет.
 Примеры функций, не имеющих производную.
Примеры функций, не имеющих производную.
1) f(x)=sign x= 
В точке х0=0 нет производной
f(0+Dx)-f(0)= 
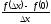 =
=  - нет предела приDх→0
- нет предела приDх→0
2) f(x)= ê х ê - в точке х0=0 нет производной (в положительной полуплоскости f¢(x)=х, в отрицательной - f¢(x)=-х). (График)
f(0+Dx)-f(0)= 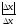 ,
, 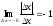 ,
, 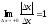 Þ нет предела при Dх→0
Þ нет предела при Dх→0
29) Физический и геометрический смыслы производной. Уравнение касательной и нормали к кривой.
1) Физический смысл производной. Если функция 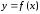 и ее аргумент
и ее аргумент  являются физическими величинами, то производная
являются физическими величинами, то производная 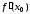 – скорость изменения переменной
– скорость изменения переменной  относительно переменной
относительно переменной  в точке
в точке 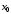 . Например, если
. Например, если  – расстояние, проходимое точкой за время
– расстояние, проходимое точкой за время 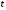 , то ее производная
, то ее производная  – скорость в момент времени
– скорость в момент времени  . Если
. Если  – количество электричества, протекающее через поперечное сечение проводника в момент времени
– количество электричества, протекающее через поперечное сечение проводника в момент времени 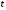 , то
, то 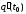 – скорость изменения количества электричества в момент времени
– скорость изменения количества электричества в момент времени  , т.е. сила тока в момент времени
, т.е. сила тока в момент времени  .
.
2) Геометрический смысл производной.
Пусть  – некоторая кривая,
– некоторая кривая,  – точка на кривой
– точка на кривой  .
. 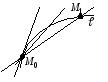
Любая прямая, пересекающая 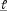 не менее чем в двух точках называетсясекущей.
не менее чем в двух точках называетсясекущей.
УРАВНЕНИЯ КАСАТЕЛЬНОЙ И НОРМАЛИ
Уравнение касательной
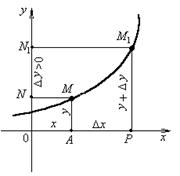
Пусть функция задается уравнением y=f(x), нужно написать уравнение касательной в точке x0. Из определения производной:
y/(x)=limΔx→0ΔyΔx
Δy=f(x+Δx)−f(x).
Уравнение касательной к графику функции: y=kx+b (k,b=const). Из геометрического смысла производной: f/(x0)=tgα=k Т.к. x0 и f(x0)∈ прямой, то уравнение касательной записывается в виде: y−f(x0)=f/(x0)(x−x0) , или
y=f/(x0)·x+f(x0)−f/(x0)·x0.

Уравнение нормали
Нормаль - это перпендикуляр к касательной (см. рисунок). Исходя из этого:
tgβ=tg(2π−α)=ctgα=1tgα=1f/(x0)
Т.к. угол наклона нормали -- это угол β1, то имеем:
tgβ1=tg(π−β)=−tgβ=−1f/(x).
Точка (x0,f(x0))∈ нормали, уравнение примет вид:
y−f(x0)=−1f/(x0)(x−x0).
30)Определение дифференцируемости функции в точке. Теоремы о связи дифференцируемости и существовании конечной производной, дифференцируемости и непрерывности.
Дифференцируемость функции в точке
Пусть функция y=f(x) определена на интервале (a,b), x-некоторая фиксированное значение аргумента из указанного интервала, 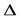 x-любое приращение аргумента.
x-любое приращение аргумента.
Опр. Функция y=f(x) называется дифференцируемой в данной точке x, если приращение  y этой функции в точке x, соответствующее приращению аргумента
y этой функции в точке x, соответствующее приращению аргумента 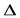 x, может быть представлено в виде
x, может быть представлено в виде  y=A
y=A 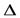 x +
x + 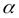
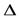 x, где А - некоторое число, не зависящее от
x, где А - некоторое число, не зависящее от 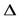 x, а
x, а 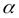 - функция аргумента
- функция аргумента  x, является бесконечно малой при
x, является бесконечно малой при 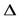 x
x 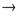 0.
0.
Связь между дифференцируемостью и непрерывностью функции.
Докажем теорему, устанавливающую связь между дифференцируемостью и непрерывностью функции.
Теорема 7.1. Если функцияy=f(x) дифференцируема в произвольной точкеx0, то она непрерывна в этой точке.
Доказательство. Пусть функция y=f(x) дифференцируема в произвольной точкеx0, т.е. имеет в этой точке производную 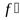 (x0). Запишем приращение функции∆yточкеx0:
(x0). Запишем приращение функции∆yточкеx0:
∆y= 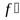 (x0) ∆ x+
(x0) ∆ x+ 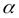 ∆ x, где
∆ x, где 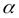 →0 при ∆ x→0 (см. доказательство теоремы 6.1).
→0 при ∆ x→0 (см. доказательство теоремы 6.1).
Пусть теперь ∆ x→0. Тогда, очевидно, и∆y→0. Но это и означает, что функцияy=f(x)непрерывна в точкеx0. Теорема доказана.
Утверждение, обратное этой теореме, неверно: из непрерывности функции в данной точке не вытекает её дифференцируемость в этой точке. Существуют функции, непрерывные в некоторой точке, но не имеющие в этой точке производной. Примером такой функции служит функция
y= 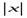 =
= 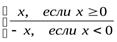
(см. рис.4).
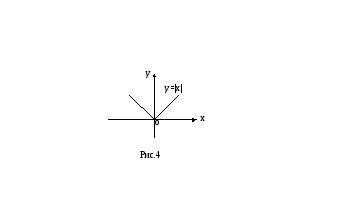
Эта функция непрерывна в точке x= 0, но не дифференцируема в ней. Действительно, приращение этой функции в точкеx= 0 есть
∆y=f(0+∆ x) ─ f(0) =f(∆ x) = 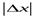 ,
,
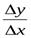 =
= 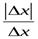 =
=  ,
,
т.е. в любой сколь угодно малой окрестности значения  отношение
отношение 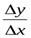 принимает два различных значения: 1 и ─1. Это означает, что предел
принимает два различных значения: 1 и ─1. Это означает, что предел 
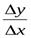 не существует, т.е. функцияy=
не существует, т.е. функцияy= 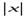 не имеет производной в точкеx= 0, а, следовательно, график функции не имеет касательной в точкеO(0;0) (поскольку угловой коэффициент касательной должен быть равен производной, но производной не существует).
не имеет производной в точкеx= 0, а, следовательно, график функции не имеет касательной в точкеO(0;0) (поскольку угловой коэффициент касательной должен быть равен производной, но производной не существует).
31)Формулы производных постоянной, суммы, произведения и частного функций.
Которым широко пользуются.
Пусть надо вычислить значение функции 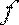 в точке
в точке  , т. е. число
, т. е. число  . Однако появилась необходимость заменить
. Однако появилась необходимость заменить  его приближенным значением
его приближенным значением 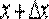 :
:
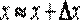 .
.
Неявно заданная функция
Если функция задана уравнением у=ƒ(х), разрешенным относительно у, то функция задана в явном виде (явная функция).
Под неявным заданием функции понимают задание функции в виде уравнения F(x;y)=0, не разрешенного относительно у.
Всякую явно заданную функцию у=ƒ (х) можно записать как неявно заданную уравнением ƒ(х)-у=0, но не наоборот.
Не всегда легко, а иногда и невозможно разрешить уравнение относительно у (например, у+2х+cosy-1=0 или 2у-х+у=0).
Если неявная функция задана уравнением F(x; у)=0, то для нахождения производной от у по х нет необходимости разрешать уравнение относительно у: достаточно продифференцировать это уравнение по x, рассматривая при этом у как функцию х, и полученное затем уравнение разрешить относительно у'.
Производная неявной функции выражается через аргумент х и функцию у.
<< Пример 21.1
Найти производную функции у, заданную уравнением х3+у3-3ху=0.

Решение: Функция у задана неявно. Дифференцируем по х равенство х3+у3-3ху=0. Из полученного соотношения
3х2+3у2· у'-3(1· у+х· у')=0
следует, что у2у'-ху'=у-х2, т. е. у'=(у-х2)/(у2-х).

Тетрадь
44)Теорема о необходимых и достаточных условиях возрастания и убывания функции
Необходимые условия возрастания (убывания) функции.
Теорема 32. Если дифференцируемая на некотором интервале 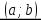 функция
функция 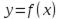 возрастает (убывает) на нем, то
возрастает (убывает) на нем, то  (
( 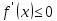 ) для всех
) для всех  .
.
Доказательство. Пусть функция 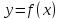 возрастаетинтервале
возрастаетинтервале 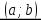 . Выберем произвольные точки
. Выберем произвольные точки 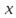 и
и 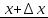 на этом интервале и рассмотрим отношение
на этом интервале и рассмотрим отношение 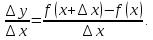
Функция 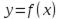 возрастает, поэтому при
возрастает, поэтому при  будет
будет 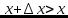 и
и  , а при
, а при 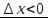 будет
будет 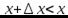 и
и 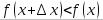 . В обоих случаях
. В обоих случаях 
так как числитель и знаменатель дроби будут иметь одинаковые знаки.
Следовательно, 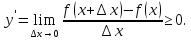
Аналогично рассматривается случай, когда функция  убывает наинтервале
убывает наинтервале  .
. 

Замечание 1. Геометрически теорема 32 означает, что касательные к графику возрастающей функции имеют острые углы с положительным направлением оси 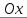 (рис. 62), а убывающие – тупые (рис. 63).
(рис. 62), а убывающие – тупые (рис. 63).
Определение.
Асимптотой кривой называется прямая, расстояние до которой от точки, лежащей на кривой, стремится к нулю при неограниченном удалении от начала координат этой точки по кривой (рис.5.10).
Асимптоты бывают вертикальные (параллельные оси Оу), горизонтальные (параллельные оси Ох) и наклонные.
 Рис. 5.10
Рис. 5.10
Вертикальные асимптоты
Определение.
Прямая 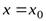 называетсявертикальной асимптотой графика функции
называетсявертикальной асимптотой графика функции 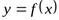 , если выполнено одно из условий:
, если выполнено одно из условий:
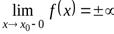 или
или 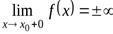 (рис.5.11)
(рис.5.11)
 Рис. 5.11
Рис. 5.11
Вертикальные асимптоты, уравнение которых х=x0 , следует искать в точках, где функция терпит разрыв второго рода, или на концах ее области определения, если концы не равны 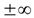 . Если таких точек нет, то нет и вертикальных асимптот.
. Если таких точек нет, то нет и вертикальных асимптот.
Например, для кривой 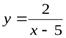 , вертикальной асимптотой будет прямая
, вертикальной асимптотой будет прямая 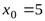 , так как
, так как 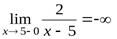 ,
,  . Вертикальной асимптотой графика функции
. Вертикальной асимптотой графика функции 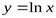 является прямая
является прямая 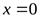 (осьОу), поскольку
(осьОу), поскольку
 .
.
Горизонтальные асимптоты
Определение.
Если при 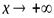 (
( 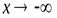 ) функция
) функция 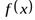 имеет конечный предел, равный числуb:
имеет конечный предел, равный числуb:
 ,
,
то прямая  есть горизонтальная асимптота графика функции
есть горизонтальная асимптота графика функции 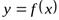 .
.
Например, для функции 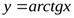 имеем
имеем
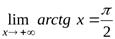 ,
, 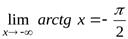 .
.
Соответственно, прямая 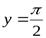 − горизонтальная асимптота для правой ветви графика функции
− горизонтальная асимптота для правой ветви графика функции 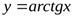 , а прямая
, а прямая 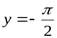 − для левой ветви.
− для левой ветви.
В том случае, если
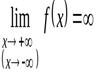 ,
,
график функции не имеет горизонтальных асимптот, но может иметь наклонные.
Наклонные асимптоты
Определение.
Прямая  называетсянаклонной асимптотой графика функции
называетсянаклонной асимптотой графика функции  при
при 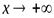 (
(  ), если выполняется равенство
), если выполняется равенство
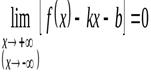 .
.
Наличие наклонной асимптоты устанавливают с помощью следующей теоремы.
Теорема.
Для того, чтобы график функции 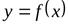 имел при
имел при 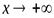 (
( 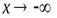 ) наклонную асимптоту
) наклонную асимптоту 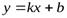 , необходимо и достаточно, чтобы существовали конечные пределы
, необходимо и достаточно, чтобы существовали конечные пределы
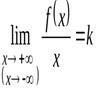 и
и 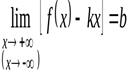 .
.
Если хотя бы один из этих пределов не существует или равен бесконечности, то кривая 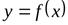 наклонной асимптоты не имеет.
наклонной асимптоты не имеет.
Замечания.
1. При отыскании асимптот следует отдельно рассматривать случаи  и
и 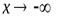 .
.
2. Если
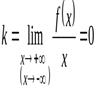 и
и  ,
,
то график функции 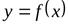 имеет горизонтальную асимптоту
имеет горизонтальную асимптоту 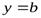 .
.
3. Если
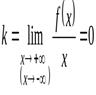 и
и 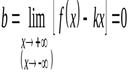 ,
,
то прямая 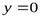 (осьОх) является горизонтальной асимптотой графика функции
(осьОх) является горизонтальной асимптотой графика функции  .
.
Из замечаний следует, что горизонтальную асимптоту можно рассматривать как частный случай наклонной асимптоты при 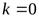 . Поэтому при отыскании асимптот графика функции рассматривают лишь два случая:
. Поэтому при отыскании асимптот графика функции рассматривают лишь два случая:
1) вертикальные асимптоты,
2) наклонные асимптоты.
Пример
Найти асимптоты графика функции  .
.
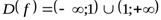 .
.
1) 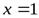 − точка разрыва второго рода:
− точка разрыва второго рода:
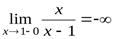 ,
, 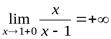 .
.
Прямая 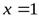 − вертикальная асимптота.
− вертикальная асимптота.
2) 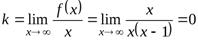 ,
,
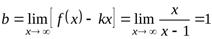 ,
,
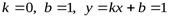 .
.
Прямая 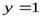 − горизонтальная асимптота. Наклонной асимптоты нет.
− горизонтальная асимптота. Наклонной асимптоты нет.
51)Основные определения функции нескольких переменных: базис в пространстве 𝑅𝑛, окрест-ность точки, открытое и замкнутое множества, область в пространстве 𝑅𝑛.
52) Область определения функции нескольких переменных, геометрический смысл, линии уровня.
Определение 1.1. Переменная z (с областью изменения Z) называется функцией двух независимых переменных х,у в множестве М, если каждой паре (х,у) из множества М по некоторому правилу или закону ставится в соответствие одно определенное значение z из Z.
Определение 1.2. Множество М, в котором заданы переменные х,у, называется областью определения функции, а сами х,у – ее аргументами.
Обозначения: z = f(x,y), z = z(x,y).
Примеры.
1. z = xy, z = x² + y² - функции, определенные для любых действительных значений х,у.
2. 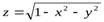 - функция, областью определения которой являются решения неравенства
- функция, областью определения которой являются решения неравенства 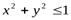 .
.
Замечание. Так как пару чисел (х,у) можно считать координатами некоторой точки на плоскости, будем впоследствии использовать термин «точка» для пары аргументов функции двух переменных, а также для упорядоченного набора чисел 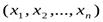 , являющихся аргументами функции нескольких переменных.
, являющихся аргументами функции нескольких переменных.
Определение 1.3. . Переменная z (с областью изменения Z) называется функцией нескольких независимых переменных  в множествеМ, если каждому набору чисел
в множествеМ, если каждому набору чисел  из множестваМ по некоторому правилу или закону ставится в соответствие одно определенное значение z из Z. Понятия аргументов и области определения вводятся так же, как для функции двух переменных.
из множестваМ по некоторому правилу или закону ставится в соответствие одно определенное значение z из Z. Понятия аргументов и области определения вводятся так же, как для функции двух переменных.
Обозначения: z = f 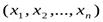 ,z = z
,z = z 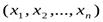 .
.
Линии и поверхности уровня.
Для функции двух переменных, заданной уравнением (1.1), можно рассмотреть множество точек (х,у) плоскости Оху, для которых z принимает одно и то же постоянное значение, то есть z = const. Эти точки образуют на плоскости линию, называемую линией уровня.
Пример.
Найдем линии уровня для поверхности z = 4 – x² - y². Их уравнения имеют вид x² + y² = 4 – c (c=const) – уравнения концентрических окружностей с центром в начале координат и с радиусами 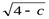 . Например, прис=0 получаем окружность x² + y² = 4 .
. Например, прис=0 получаем окружность x² + y² = 4 .
Для функции трех переменных u = u (x, y, z) уравнение u (x, y, z) = c определяет поверхность в трехмерном пространстве, которую называютповерхностью уровня.
Пример.
Для функции u = 3x + 5y – 7z –12 поверхностями уровня будет семейство параллельных плоскостей, задаваемых уравнениями
3x + 5y – 7z –12 + с = 0.
53) Предел и непрерывность функции нескольких переменных.
Введем понятие δ-окрестности точки М0 (х0 , у0) на плоскости Оху как круга радиуса δ с центром в данной точке. Аналогично можно определить δ-окрестность в трехмерном пространстве как шар радиуса δ с центром в точке М0 (х0 , у0 , z0). Для n-мерного пространства будем называть δ-окрестностью точки М0 множество точек М с координатами  , удовлетворяющими условию
, удовлетворяющими условию
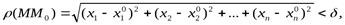
где 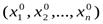 - координаты точкиМ0. Иногда это множество называют «шаром» в n-мерном пространстве.
- координаты точкиМ0. Иногда это множество называют «шаром» в n-мерном пространстве.
Определение 1.4. Число А называется пределом функции нескольких переменных f  в точкеМ0, если
в точкеМ0, если 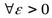
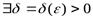 такое, что | f(M) – A| < ε для любой точки М из δ-окрестности М0.
такое, что | f(M) – A| < ε для любой точки М из δ-окрестности М0.
Обозначения:  .
.
Необходимо учитывать, что при этом точка М может приближаться к М0, условно говоря, по любой траектории внутри δ-окрестности точки М0. Поэтому следует отличать предел функции нескольких переменных в общем смысле от так называемых повторных пределов, получаемых последовательными предельными переходами по каждому аргументу в отдельности.
Примеры.
1. Покажем, что функция 
 не имеет предела приМ→О(0,0). Действительно, если в качестве линии, по которой точка М приближается к началу координат, выбрать прямую у = х, то на этой прямой
не имеет предела приМ→О(0,0). Действительно, если в качестве линии, по которой точка М приближается к началу координат, выбрать прямую у = х, то на этой прямой  . Если же траекторией движения считать прямуюу = 2х, то
. Если же траекторией движения считать прямуюу = 2х, то 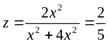 . Следовательно, предел в точке (0,0) не существует.
. Следовательно, предел в точке (0,0) не существует.
2. Найдем повторные пределы функции 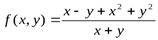 прих→0, у→0.
прих→0, у→0.  ,
, 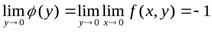 . Если же произвести предельные переходы в обратном порядке, получим:
. Если же произвести предельные переходы в обратном порядке, получим: 
 Таким образом, повторные пределы оказались различными (откуда следует, конечно, что функция не имеет в точке (0,0) предела в обычном смысле).
Таким образом, повторные пределы оказались различными (откуда следует, конечно, что функция не имеет в точке (0,0) предела в обычном смысле).
Замечание. Можно доказать, что из существования предела в данной точке в обычном смысле и существования в этой точке пределов по отдельным аргументам следует существование и равенство повторных пределов. Обратное утверждение неверно.
54) Частные производные первого порядка функции нескольких переменных. Необходимое усло-вие дифференцируемости.
Определение. Если существует  , то он называется частной производной (первого порядка) функции
, то он называется частной производной (первого порядка) функции 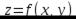 по переменной
по переменной 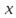 и обозначается
и обозначается
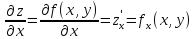
Аналогично определяется частная производная по переменной y:
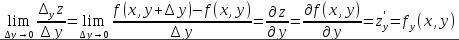
Метод математической индукции.
В основе метода математической индукции лежит принцип математической индукции.
Он заключается в следующем: некоторое утверждение справедливо для всякого натурального n, если
оно справедливо для n = 1 и
из справедливости утверждения для какого-либо произвольного натурального n = k следует его справедливость для n = k+1.
То есть, доказательство по методу математической индукции проводится в три этапа:
во-первых, проверятся справедливость утверждения для любого натурального числа n (обычно проверку делают для n = 1);
во-вторых, предполагается справедливость утверждения при любом натуральном n=k;
в-третьих, доказывается справедливость утверждения для числа n=k+1, отталкиваясь от предположения второго пункта.
к примеру, формула суммы n первых членов арифметической прогрессии формула,  формула бинома Ньютона
формула бинома Ньютона 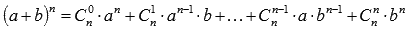
2) Понятие функции. Способы задания функций. Примеры. Элементарные функции, гиперболи-ческие функции. Обратные, неявные, параметрически заданные функции. Циклоида, астроида.
Фу́нкция — математическое понятие, отражающее однозначную парную связь элементов одного множества с элементами из другого множества
Пусть даны две переменные х и y с областями изменения Х и Y. Переменная y называется функцией от х, если по некоторому правилу или закону каждому значению 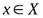 ставится в соответствие одно определенное значение
ставится в соответствие одно определенное значение 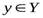 .
.
Для указания этого факта, что y есть функция от х, пишут: 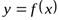 ,
, 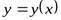 ,
, 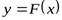 и т.п.
и т.п.
Можно также сказать, что функция f отображает множество Х на множество Y. Это обозначается так 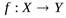 (рис.)
(рис.)
 Рис. 1.1
Рис. 1.1
Переменная х называется независимой переменной или аргументом.
Переменная y называется зависимой переменной или функцией.
Относительно самих величин х и y говорят, что они находятся в функциональной зависимости.
Способы задания функции
1.Табличный способ.При этом способе в определенном порядке выписываются ряд значений независимой переменной 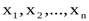 и соответствующие им значения функции
и соответствующие им значения функции 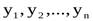 . Таковы, например, таблицы логарифмов, таблицы значений тригонометрических функций и т.д. Табличный способ очень распространен в технике, естествознании и т.п. Численные результаты последовательных наблюдений какого-либо процесса или явления выписываются в виде таблицы
. Таковы, например, таблицы логарифмов, таблицы значений тригонометрических функций и т.д. Табличный способ очень распространен в технике, естествознании и т.п. Численные результаты последовательных наблюдений какого-либо процесса или явления выписываются в виде таблицы
| x | 1 | 2 | 3 | 4 |
| y | 1 | 4 | 9 | 16 |
2.Графический способ.Графикомфункцииy=f(x) называется множество всех точек плоскости, координаты которых удовлетворяют данному уравнению. Это может быть некоторая кривая, в частности прямая, множество точек на плоскости.
Преимущество – наглядность, недостаток – нет возможности точно определить значения аргумента. В технике и физике часто он является единственно доступным способом задания функции, например, при пользовании самопишущими приборами, которые автоматически записывают изменение одной величины относительно другой (барограф, термограф и др.).
3. Аналитический способ.По этому способу функция задается аналитически, с помощью формулы. Такой способ дает возможность по каждому численному значению аргумента х найти соответствующее ему численное значение функции у точно или с некоторой точностью.
При аналитическом способе функция может быть задана и несколькими разными формулами. Например, функция (с помощью некоторого правила)
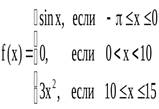
4. Словесный способ.Этот способ состоит в том, что функциональная зависимость выражается словами. Например, функция Е(х) – целая часть числа х, функция Дирихле, функция Римана,n!,r(n) – число делителей натурального числаn.
Пример: Исследовать функцию f(x)={{x}^{2}} на четность.
Для заданной функции
f (- x )= 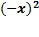 =
= 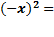 f ( x )
f ( x )
Значит, эта функция четная.
Ответ Функция четная.
Функция f(x)= sin x является периодической, так как
f( x+2π)=sin (x+2π)=sin x
Период этой функции T=2π
Основные элементарные функции+тетрадь
1. Степенная функция
 ,
,  .
.
2. Показательная функция
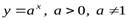 .
.
3. Логарифмическая функция
 .
.
4. Тригонометрические функции
 .
.
5. Обратные тригонометрические функции
 .
.

Пусть функция y=f(x) определена на множестве D, а E — множество её значений. Обратная функция по отношению к функции y=f(x) — это функция x=g(y), которая определена на множестве E и каждому y ∈ E ставит в соответствие такое значение x ∈ D, что f(x)=y.
Таким образом, область определения функции y=f(x) является областью значений обратной к ней функции, а область значений y=f(x) — областью определения обратной функции.
Чтобы найти функцию, обратную данной функции y=f(x), надо:
1) В формулу функции вместо y подставить x, вместо x — y:
x=f(y).
2) Из полученного равенства выразить y через x:
y=g(x).
Пример.
Найти функцию, обратную функции y=2x-6.
1) x=2y-6
2) -2y=-x-6
y=0,5x+3.
Функции y=2x-6 и y=0,5x+3 являются взаимно обратными.
Под неявным заданием функции понимают задание функции в виде уравнения F(x;y)=0, не разрешенного относительно у.
Всякую явно заданную функцию у=ƒ (х) можно записать как неявно заданную уравнением ƒ(х)-у=0, но не наоборот.
Не всегда легко, а иногда и невозможно разрешить уравнение относительно у (например, у+2х+cosy-1=0 или 2у-х+у=0).
Если неявная функция задана уравнением F(x; у)=0, то для нахождения производной от у по х нет необходимости разрешать уравнение относительно у: достаточно продифференцировать это уравнение по x, рассматривая при этом у как функцию х, и полученное затем уравнение разрешить относительно у'.
Производная неявной функции выражается через аргумент х и функцию у.
Связь между аргументом и функцией может быть записана через дополнительную переменную, называемую параметром, то есть в виде системы, в которой прописывается зависимость аргумента от параметра и зависимость функции от того же параметра:
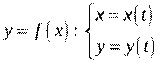 , где
, где 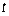 – это параметр,
– это параметр, 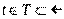 .
.
В этом случае функция называетсяфункцией, заданной параметрически.
График функции
Графиком функции y = f(x) называется множество всех точек, у которых абсциссы принадлежат области определения функции, а ординаты равны соответствующим значениям функции.
Другими словами, график функции y = f (х) - это множество всех точек плоскости, координаты х, у которых удовлетворяют соотношению y = f(x).
3) Декартовы и полярные координаты на плоскости. Примеры кривых в полярных координатах.
Декартова система координат на плоскости определяется некоторой ее точкой O и базисом из двух векторов, параллельных плоскости. Точка Oназывается началом координат. Прямые, проведенные через начало координат в направлении базисных векторов, называются осями координат. Они лежат в плоскости и называются осями абсцисс и ординат. Каждая ось координат является числовой осью с началом в точке O, положительным направлением, совпадающим с направлением соответствующего базисного вектора, и единицей длины, равной длине этого вектора.
Координатами точки M называются координаты вектора OM (радиус–вектора) (см. рис. 1).

Если базис ортонормированный, то связанная с ним декартова система координат называется прямоугольной.
На плоскости часто употребляется также полярная система координат (рис. 2).

Она определяется точкой O, называемой полюсом, и лучом, исходящим из полюса, называемым полярной осью. Полярными координатами ρ и j точкиM называются расстояние ρ от полюса до точки M ( ρ = |OM|) и угол j между полярной осью и вектором OM (рис. 2). Угол j называется полярным углом, измеряется в радианах и отсчитывается от полярной оси против часовой стрелки. Полярные координаты точки O: ρ = 0, угол j не определен. У остальных точек ρ > 0 и угол j определен с точностью до 2π. Обычно полагают 0 ≤ j < 2 π или − π < j ≤ π.
Если полюс совпадает с началом прямоугольной декартовой системы координат, а полярная ось — с положительной частью оси абсцисс, то декартовы координаты x и y точки M выражаются через ее полярные координаты ρ и j формулами
x = ρcosj y = ρsinj .
4)Линейная интерполяция. Интерполяционный многочлен Лагранжа.
Лине́йная интерполя́ция — интерполяция алгебраическим двучленом P1(x) = ax + b функции f, заданной в двух точках x0 и x1 отрезка [a, b]. В случае, если заданы значения в нескольких точках, функция заменяется кусочно-линейной функцией.
Простейшим и часто используемым видом локальной интерполяции является линейная интерполяция. Она состоит в том, что заданные точки (xi,yi) при (i = 0. 1, ..., n) соединяются прямолинейными отрезками, и функция f(x) приближается ломаной с вершинами в данных точках.
Уравнения каждого отрезка ломаной в общем случае разные. Поскольку имеется n интервалов (xi-1,xi), то для каждого из них в качестве уравнения интерполяционного многочлена используется уравнение прямой, проходящей через две точки. В частности, для i-го интервала можно написать уравнение прямой, проходящей через точки(xi-1,yi-1) и (xi,yi), в виде
 =
= 
5 )Определение числовой последовательности. Определение монотонной, ограниченной, неогра-ниченной последовательностей. Определение последовательности, ограниченной сверху, ограниченной снизу. Теорема о свойстве верхней грани.
Числовая последовательность — это последовательность элементов числового пространства.
Последовательность 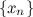 называется монотонно возрастающей, если для любого
называется монотонно возрастающей, если для любого 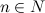 ,
, 
пример
Последовательность 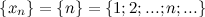 является возрастающей, так как для любого
является возрастающей, так как для любого 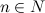 ,
, 
Дата: 2019-02-19, просмотров: 465.