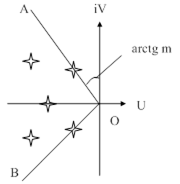
Рис. 90. Иллюстрация к понятию расширенных частотных характеристик.

При разработке систем автоматического регулирования критерии качества применяются не только для анализа готовых систем, но и, что особенно важно, на стадии их расчета, когда параметры системы выбираются с учетом требований, предъявляемых к качеству переходного процесса.

Одним из наиболее удобных для таких расчетов показателей качества является степень колебательности , которая вводится в расчеты с помощью расширенных частотных характеристик.

Рассмотрим две плоскости комплексного переменного: плоскость корней характеристического уравнения и плоскость АФХ. Обычные частотные характеристики получаются из передаточной функции объекта путем подстановки вместо 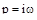. При этом годограф АФХ является отображением мнимой оси плоскости корней на плоскость АФХ, т.к. именно вдоль этой оси .

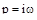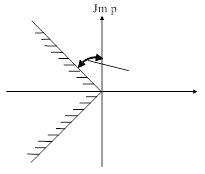
Рассмотрим в плоскости корней два луча (рис. 90): ОА и ОВ под углом , где  - заданная степень колебательности. Комплексная переменная p на этих лучах имеет координаты 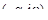, где 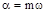. Подставив в передаточную функцию 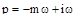, получим 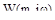, которая называется расширенной амплитудно-фазовой характеристикой (РАФХ). Т.о. годограф  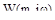для положительных частот является отображением луча АО на плоскость АФХ.

Как и в обычных частотных характеристиках, выделяют расширенную амплитудно-частотную характеристику и расширенную фазо-частотную характеристику (РАЧХ, РФЧХ), которые находят аналогично обычным частотным характеристикам.

РАФХ: ;

РАЧХ: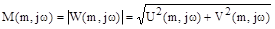

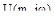– действительная часть;

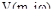 – мнимая часть;

РФЧХ: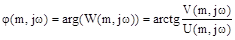

Пример.

Для примера найдем расширенные частотные характеристики апериодического вена первого порядка. Обычные частотные характеристики этого звена нам известны. Для вывода в передаточной функции этого звена произведем замену 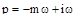  и выделим модуль и аргумент:

;

; ,

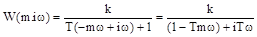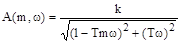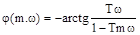причем

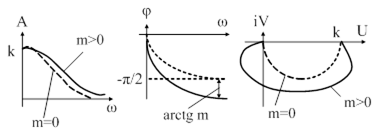
Рис. 91.  Обычные и расширенные частотные характеристики апериодического звена I-го порядка.

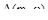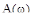Сравнение графиков обычных и расширенных частотных характеристик (рис. 91) показывает, что для любой частоты значения  и  больше по абсолютной величине, чем соответствующие значения  и 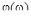. Поэтому годограф  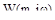проходит шире, чем годограф .

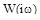Рис. 92. Иллюстрация к понятию метода РАФХ.

Необходимо отметить еще одну особенность 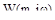: если провести касательные к годографам АФХ и РАФХ в точке 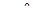, то угол между этими касательными будет равен 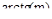, причем касательная к годографу АФХ составляет с осью абсцисс 90⁰.

Метод РАФХ.

Согласно критерия Найквиста, если АФХ устойчивой разомкнутой системы проходит через критическую точку , то замкнутая система находится на границе устойчивости. В качестве границы устойчивости выступает мнимая ось комплексной плоскости корней характеристического уравнения. Введение степени колебательности  для получения РАФХ означает введение новой границы устойчивости вместо мнимой оси лучи AOB (рис. 92).

Аналогично критерия Найквиста можно сформулировать условия для достижения замкнутой системой заданной степени колебательности .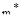

Если разомкнутая система имеет степень колебательности не ниже заданного значения 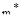, то замкнутая система обладает заданной степенью колебательности 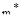, если РАФХ разомкнутой системы проходит через критическую точку ; если РАФХ разомкнутой системы не охватывает критическую точку , то замкнутая система имеет степень колебательности выше заданного значения .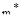

Если РАФХ разомкнутой системы имеет степень колебательности ниже заданного значения 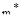, то замкнутая система будет обладать заданным значением степени колебательности 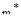, если РАФХ разомкнутой системы охватывает критическую точку столько раз, сколько корней характеристического уравнения располагается правее лучей АОВ. Из сформулированного условия можно записать:

;

Учитывая, что 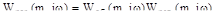; (разомкнутая система будет представлена последовательным соединением объекта и регулятора).

Подставим в предыдущее уравнение и получим:

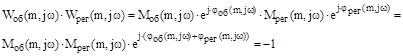
Отсюда:

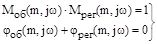
Частотные характеристики объекта и заданная степень колебательности являются исходными данными для расчета АСР, характеристики регулятора являются функцией неизвестных параметров настройки 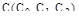. Тогда система уравнений запишется в виде:

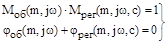                                  (13)

Анализ системы уравнений показывает, что одного заданного значения степени колебательности 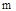 является недостаточно для расчета настроек регулятора. Для определения оптимальных настроек вводится новый критерий – интегральный квадратичный критерий. Задача будет формулироваться так:

Рассчитать оптимальные настройки регулятора из условия минимума интегрального квадратичного критерия при заданной степени колебательности. Эта задача решается в два этапа.

На первом этапе задача выбора оптимальных настроек регулятора сводится к решению системы уравнений (13), неизвестными в которых являются вектор параметров настроек 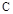 и рабочая частота .

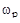Очевидно, что для регуляторов с двумя или тремя параметрами настроек эта система уравнений имеет бесчисленное множество решений. Это означает, что одного только ограничения по степени колебательности недостаточно для однозначного выбора оптимальных настроек регулятора и требуется какой-либо второй критерий качества.

При использовании метода расширенных частотных характеристик таким критерием выбран интегральный квадратичный критерий, для которого оптимальные настройки должны обеспечивать минимальное значение.

Таким образом на втором этапе расчета оптимальные настройки выбирают по минимуму интегрального критерия из числа тех настроек, которые обеспечивают заданную степень колебательности системы, т.е. являются решением уравнений (13). Рассмотрим подробнее методику выбора оптимальных настроек для типовых регуляторов.

П – регулятор имеет один параметр настройки 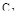. Его расширенные частотные характеристики совпадают с обычными, т.е.

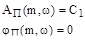
В этом случае уравнения (13) принимают вид:

Рабочая частота 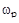 определяется из второго уравнения системы, а затем из первого находится оптимальная настройка .

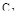ПИ – регулятор – регулятор с двумя параметрами настроек  и . Его расширенные частотные характеристики выводятся из передаточной функции подстановкой :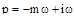

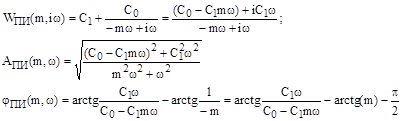
с учетом того, что .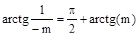

После подстановки полученных выражений в уравнения (13) выводятся формулы для настроек регуляторов в следующем виде:

.

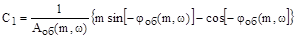
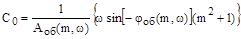Рис. 93. Плоскость параметров настроек ПИ-регулятора.

Поскольку в формулы для настроек входит неизвестная переменная 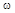, то, следовательно, существует бесчисленное множество настроек  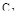и , обеспечивающих заданную степень колебательности в данной АСР, причем каждой паре настроек соответствует своя рабочая частота.

Если в плоскости параметров 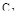,  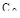построить геометрическое место точек, соответствующих определенной степени колебательности 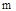, получим кривую, называемую кривой равной колебательности (рис. 93).

Принимая различные значения m, получим семейство кривых равной колебательности, каждая из которых разбивает плоскость параметров на две области: настройки, лежащие под кривой 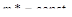, обеспечивает себе степень колебательности, больше ; область, расположенная под этой кривой, соответствует степени колебательности, меньшей, чем 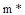. Очевидно, что кривая  разбивает плоскость параметров настроек регулятора на области устойчивой и неустойчивой работы АСР.

Точки, лежащие на кривой равной колебательности, соответствует разным значениям рабочей частоты, причем при движении вдоль кривой слева направо частота увеличивается.

Сравним между собой процессы регулирования, соответствующие различным точкам на кривой равной колебательности (рис. 93, 94).

Рис. 94. Примеры переходных процессов в АСР с ПИ-регулятором.

В точке 1 отсутствует интегральная составляющая в законе регулирования  и в процессе регулирования появляется статическая ошибка. При незначительной интегральной составляющей (точка 2) статическая ошибка равна нулю, но скорость ее устранения мала и переходный процесс характеризуется затянутым «хвостом». Увеличение интегральной составляющей ускоряет устранение статической ошибки, но сопровождается уменьшением рабочей частоты (движением влево по кривой равной колебательности) и некоторым ростом динамической ошибки (точка 4). Переход через вершину кривой влево (точка 5) резко ухудшает качество переходного процесса, так как одновременно с уменьшением  уменьшается и .

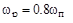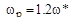Расчет интегрального квадратичного критерия для рассмотренных процессов показывает, что его минимум соответствует точке на кривой равной колебательности на правой ветви вблизи вершины. На практике рекомендуется выбирать рабочую частоту из соотношения:  или , где  – частота, соответствующая П – регулятору (точка 1);  - частота, соответствующая вершине кривой равной колебательности.

Таким образом, методика расчета оптимальных настроек ПИ – регулятора сводится к следующему:

 - расчет расширенных частотных характеристик объекта для заданной степени колебательности ;

- расчет и построение кривой равной колебательности  в плоскости параметров 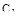 и 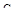 по формулам;

- выбор рабочей частоты  и соответствующих ей оптимальных настроек.

ПД – регулятор так же, как и ПИ – регулятор, имеет два параметра настроек –  и 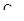, поэтому процедура расчета этих регуляторов аналогична. В соответствии с изложенной методикой выведем расчетные формулы для ПД – регулятора.

Расширенные частотные характеристики ПД – регулятора имеют вид:

;

;

.

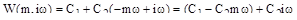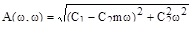Решение системы уравнений дает следующие выражения для настроек регулятора:

,

.

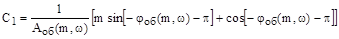Рис. 95. Плоскость параметров настроек ПД – регулятора.

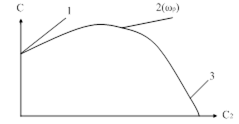
Кривая равной колебательности рассчитывается по последним формулам и строится в плоскости 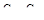. Типичная картина разбиения плоскости параметров ПД – регулятора кривыми равной колебательности приведена на рис. 95.

Движение вдоль кривой вправо, при котором растет дифференциальная настройка, сопровождается увеличением рабочей частоты и, следовательно, уменьшением динамической ошибки. Однако при этом статическая ошибка сначала уменьшается (пока растет пропорциональная составляющая), а затем увеличивается (на правой ветви кривой).

Рис. 96. Примеры процессов регулирования.

Таким образом, оптимальные настройки ПД – регулятора соответствуют вершине кривой равной колебательности.

На рис. 96 приведены примеры переходных процессов в АСР с ПД – регулятором при различных настройках.

ПИД – регулятор имеет три параметра настроек 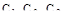 и поэтому его расчет по методу расширенных частотных характеристик несколько сложнее, чем расчет регуляторов с двумя параметрами.

Расширенные частотные характеристики ПИД – регулятора:

;

; ;

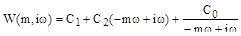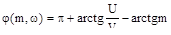где .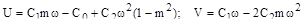

Решение системы уравнений с учетом последних формул дает выражения для расчета двух настроек как функции третьей настройки, например:

;

,

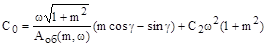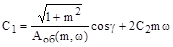где .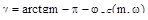

Для ПИД – регулятора вместо плоскости параметров настроек мы имеем трехмерное пространство. В этом случае определение оптимальных настроек производится в следующем порядке.

Рис. 97. Плоскость параметров настроек ПИД – регулятора.

Задаваясь различными значениями настройки 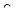, по последним формулам рассчитываем кривые равной колебательности в плоскости  (рис. 97). Характер этих кривых аналогичен рассмотренной ранее кривой для ПИ – регулятора, который получается как частный случай из ПИД – регулятора при . Условно оптимальные настройки находятся также как и для ПИ – регулятора.

Рис. 98. Примеры процессов регулирования.

Сравнение между собой оптимальных процессов регулирования для разных значений 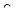 показывает, что введение дифференциальной составляющей в закон регулирования (по сравнению с ПИ – регулятором) существенно улучшает качество переходных процессов (рис. 98).

Однако, начиная с некоторых значений , дальнейшее его увеличение малоэффективно. поэтому окончательный выбор оптимального значения 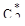 и соответствующих ему  и 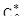 должен производиться на основе непосредственного сравнения качества процессов регулирования по интегральному квадратичному критерию.