Под синтезом системы автоматического управления понимается направленный расчет, имеющий конечной целью отыскание рациональной структуры системы и установление оптимальных величин параметров ее отдельных звеньев.

При инженерном синтезе системы автоматического управления необходимо обеспечить, во-первых, требуемую точность и, во-вторых, приемлемый характер переходных процессов.

Решение первой задачи в большинстве случаев сводится к определению требуемого общего коэффициента разомкнутой системы и, в случае необходимости, - вида корректирующих средств, повышающих точность системы (комбинированное управление, изодромные механизмы и т.д.). Эта задача может решаться при помощи определения ошибок в типовых режимах на основе тех критериев точности, которые были рассмотрены в главе 3. Решение этой задачи, как правило, не сопряжено с трудностями принципиального или вычислительного характера, так как критерии точности достаточно просты для их практического использования. В сложных случаях можно прибегать к помощи моделирования. Решение оказывается сравнительно простым вследствие необходимости установления значений относительно небольшого числа параметров. В простейшем случае необходимо найти только коэффициент передачи разомкнутой системы.

Решение второй задачи – обеспечение приемлемых переходных процессов - оказывается почти всегда более трудным вследствие большого числа варьируемых параметров и многозначности решения задачи демпфирования системы. Поэтому существующие инженерные методы часто ограничиваются решением только второй задачи.

В настоящее время для целей синтеза систем автоматического управления широко используются вычислительные машины, позволяющие производить полное или частичное моделирование проектируемой системы. При таком моделировании становится возможным наиболее полно исследовать влияние различных факторов нелинейности, зависимость параметров от времени и т.д.

Однако моделирование на вычислительных машинах не может заменить расчетных методов проектирования, которые во многих случаях позволяют исследовать вопрос в общем виде и среди многих решений найти оптимальное. Поэтому, несмотря на развитие и распространение машинных методов синтеза, теория должна располагать собственными методами, которые дополняли бы моделирование и являлись бы теоретической базой при отыскании оптимального решения.

Корневой метод

Наиболее простой метод разработал Т.Н.Соколов. Сущность его сводится к следующему.

Пусть имеется характеристическое уравнение системы:

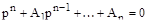                         (10)

С точки зрения скорейшего затухания переходного процесса важно, чтобы вещественные части всех корней характеристического уравнения были наибольшими. Сумма вещественных частей всех корней численно равна первому коэффициенту характеристического уравнения. Поэтому при заданной величине этого коэффициента наиболее лучшие результаты получаются при равенстве вещественных частей всех корней. Однако расчеты и исследования построенных систем показывают, что стремление удовлетворить поставленному требованию приводит к совершенно нереальным конструктивным характеристикам отдельных звеньев. Эти расчеты и исследования показывают, что из общего числа корней характеристического уравнения всегда можно выделить два или три корня с меньшей по абсолютному значению вещественной частью, которые и определяют ход основного процесса. Остальные же корни характеризуют быстро затухающие составляющие, оказывающие влияние только на начальной стадии переходного процесса.

Примем, что основной характер переходного процесса определяется двумя корнями. тогда уравнение (10) удобно представить в виде

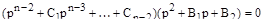
 (11)

Второй сомножитель (11) и будет определять основной характер процесса.

Для уменьшения погрешностей проектируемой системы важно, чтобы коэффициент  в основном множителе имел возможно большую величину. Однако чрезмерное увеличение приводит к колебательному характеру переходного процесса.

Оптимальное соотношение между коэффициентам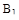и  и  определяется из условия получения затухания за один период 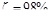 (см. Бесекерский стр. 206), которому соответствует выражение

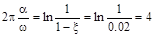                     (12)

где  и 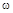 – вещественная и мнимая части комплексного корня, характеризующего основной процесс.

Учитывая соотношения:

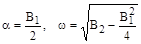
из (12) можно получить: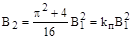

Множитель 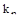, определяющий соотношение между коэффициентами основного множителя характеристического уравнения, является критерием переходного режима, зависящим от выбранной степени затухания. Последняя формула показывает желаемое соотношение между коэффициентами характеристического уравнения, к которому надо стремится при проектировании системы. Это должно осуществляться введением различных корректирующих средств.

Из (12) можно также получить требуемые соотношения между мнимой и вещественной частями корня (колебательность):

.

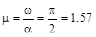Метод корневых годографов.

Качество системы управления с точки зрения быстродействия и запаса устойчивости может характеризоваться расположением корней числителя и знаменателя передаточной функции замкнутой системы, т.е. расположением нулей и полюсов передаточной функции.

Зная эти корни, можно изобразить их расположение на комплексной плоскости корней. При расчете системы целесообразно проследить, как меняется картина расположения корней при изменении отдельных параметров, например коэффициента передачи разомкнутой системы, постоянных времени корректирующих цепей и т.д., с целью установления оптимальных значений этих параметров.

При плавном изменении значения какого либо параметра корни будут перемещаться на плоскости корней, прочерчивая некоторую кривую, которую будем называть корневым годографом или траекторией корней. Построив траектории всех корней, можно выбрать такое значение варьируемого параметра, которое соответствует наилучшему расположению корней.

Один из способов построения траекторий корней заключается в следующем. Пусть имеется передаточная функция замкнутой системы:

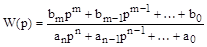
Полюсы передаточной функции, т.е. корни знаменателя, обозначим через 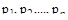, а нули (корни числителя) – через .

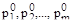Коэффициенты числителя и знаменателя определенным образом выражены через параметры объекта, управляющего устройства и корректирующих устройств. Если нужно выбрать величину какого-либо параметра 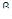 (постоянная времени, коэффициент усиления и т.д.), входящего как угодно в коэффициенты передаточной функции, то необходимо принять некоторые постоянные значения для всех остальных параметров, а для искомого параметра  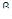задавать различные числовые значения  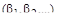внутри реально возможных пределов изменения этого параметра в данной системе. Для каждого из этих вариантов необходимо затем вычислить корни числителя и знаменателя. Результаты вычислений можно свести в таблицу, на основании которой легко строятся все траектории корней.

Если нужно выбрать два или несколько параметров системы, то такого рода вычисления нужно проделать несколько раз, меняя каждый раз один параметр при заданных значениях всех остальных.

Вычисление корней при этом можно производить при помощи стандартных программ для цифровых машин с выводом корневого годографа на экран дисплея.